Вопрос №8. Купола. Особенности расчета.
 Элемент купола, ограничен двумя меридиональными и двумя кольцевыми сечениями, нах-ся под возд усилий: меридионального, кольцевого и касательного N1,N2,Sотнесенных к единице длины сечения. При осесимметричной нагрузке S=0.
Элемент купола, ограничен двумя меридиональными и двумя кольцевыми сечениями, нах-ся под возд усилий: меридионального, кольцевого и касательного N1,N2,Sотнесенных к единице длины сечения. При осесимметричной нагрузке S=0.

 Введем обознач: Ψ-текущ угловая координата, QΨ-суммарная нагрузка на верхний сегмент оболочки, огранич чесением а-а.
Введем обознач: Ψ-текущ угловая координата, QΨ-суммарная нагрузка на верхний сегмент оболочки, огранич чесением а-а.  .R2-радиус кривизны оболочки в кольцевом напр. Горизонт проекция N1 наз-ся распором Hи опред:
.R2-радиус кривизны оболочки в кольцевом напр. Горизонт проекция N1 наз-ся распором Hи опред:  .Распор вопринимается нижним опроным кольцом. При вертикальной нагрузке распред по пов-ти купола (g-собств вес комнтрукции покрытия) нормальная составляющая ее в точках с углом Ψ равна
.Распор вопринимается нижним опроным кольцом. При вертикальной нагрузке распред по пов-ти купола (g-собств вес комнтрукции покрытия) нормальная составляющая ее в точках с углом Ψ равна  ,
,  -площадь шарового сегмента.
-площадь шарового сегмента.  . подставл Sв Q, где g-нагрузка на сегмент. Тогда
. подставл Sв Q, где g-нагрузка на сегмент. Тогда 
 .При Ψ=0
.При Ψ=0  (сжатие)
(сжатие)  (сжатие). При Ψ=π/2,
(сжатие). При Ψ=π/2,  (сжатие)
(сжатие)  (растяжение). Кольцевое сечение в кот N2=0 определяется углом 51°49''. Аналогично можно получить решениепри снеговой нагрузке "Р". Нагрузка на единицу площади купола
(растяжение). Кольцевое сечение в кот N2=0 определяется углом 51°49''. Аналогично можно получить решениепри снеговой нагрузке "Р". Нагрузка на единицу площади купола  ,а нормальная составляющая
,а нормальная составляющая  .Суммарная снеговая нагрузка:
.Суммарная снеговая нагрузка:  тогда
тогда 
 . При Ψ=0
. При Ψ=0  (сжатие), Ψ=90°
(сжатие), Ψ=90°  (растяжение), Ψ=45°
(растяжение), Ψ=45° 
 Вопрос №9. Конструктивные особенности пологих оболочек положительной Гауссовой кривизны на прямоугольном плане.
Вопрос №9. Конструктивные особенности пологих оболочек положительной Гауссовой кривизны на прямоугольном плане.
 Такие оболочки состоят из тонкостенной изогнутой в двух направлениях плиты, сопряженной по краям с контурными элементами - диафрагмами. В зависимости от отношения f/l2 оболочки м.б. пологими или подъемистыми. В пологих обол угол между касательной к поверхн и плоскостью основания любой точке не превышает 18°. Отношение fк l2 должно быть не более 1/5. Уравнение поверхности имеет вид
Такие оболочки состоят из тонкостенной изогнутой в двух направлениях плиты, сопряженной по краям с контурными элементами - диафрагмами. В зависимости от отношения f/l2 оболочки м.б. пологими или подъемистыми. В пологих обол угол между касательной к поверхн и плоскостью основания любой точке не превышает 18°. Отношение fк l2 должно быть не более 1/5. Уравнение поверхности имеет вид  .Поверхность рассматриваемых оболочек м.б. очерчена в виде сферы(б), тора(в), эллиптического параболоида(г). Уравнения этих поверхностей имеют вид. а)
.Поверхность рассматриваемых оболочек м.б. очерчена в виде сферы(б), тора(в), эллиптического параболоида(г). Уравнения этих поверхностей имеют вид. а)  б)
б)  в)
в)  . x,y,z -текущие координаты, r1,r2-радиусы кривизны в направлении осей x,y. Сферическая пов-ть примен для квадр в плане обол. Торовые для обол на прямоуг плане. Монолитн обол пролетом 24-60м выполняют гладкими. Армирование средней зоны назнач конструктивно в количестве 0,2% от площади бетона. Моменты возник в обол невелики и могут быть легко восприняты конструктивной арматурой. Сборные обол собираются из отдельных элементов. Размеры панелей в сборн обол приним 3х3, 3х6 и 3х12. толщина 30-50мм. Стыки между панел выполняются путем заполнения бетоном.
. x,y,z -текущие координаты, r1,r2-радиусы кривизны в направлении осей x,y. Сферическая пов-ть примен для квадр в плане обол. Торовые для обол на прямоуг плане. Монолитн обол пролетом 24-60м выполняют гладкими. Армирование средней зоны назнач конструктивно в количестве 0,2% от площади бетона. Моменты возник в обол невелики и могут быть легко восприняты конструктивной арматурой. Сборные обол собираются из отдельных элементов. Размеры панелей в сборн обол приним 3х3, 3х6 и 3х12. толщина 30-50мм. Стыки между панел выполняются путем заполнения бетоном.
Вопрос №10. Основы расчета пологих оболочек Гауссовой кривизны на прямоугольном плане по безмоментной теории.
Большая поверхность оболочек сжата а изгибающие моменты почти равны нулю. Это позволяет использовать безмоментную теорию расчета. Система уравнений равновесия полученная из суммы проекций нагрузки и внутренних усилий имеет вид 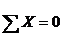
 ,
, 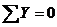
 ,
, 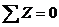
 . x,y - декартовы коорд на горизонт проекции поверхности обол. N-нормальные и касательные усилия. q=const - интенсивность нормальной нагрузки. Диафрагмы считаются гибкими из своей плоскости, а в своей плоскости недеформируемыми. Этим определяются условия на контуре оболочки при
. x,y - декартовы коорд на горизонт проекции поверхности обол. N-нормальные и касательные усилия. q=const - интенсивность нормальной нагрузки. Диафрагмы считаются гибкими из своей плоскости, а в своей плоскости недеформируемыми. Этим определяются условия на контуре оболочки при  и
и 

 .Для оболочек на прямоуг плане система ур точного решения не имеет, поэтому на практике примен приближенные методы расчета: метод конечных разностей, метод конечных элементов, метод коллокаций. Для решения системы уравнений удобен прием, основанный на использовании функции напряжений φ(х,у), подобранной таким образом чтобы выполнялись условия
.Для оболочек на прямоуг плане система ур точного решения не имеет, поэтому на практике примен приближенные методы расчета: метод конечных разностей, метод конечных элементов, метод коллокаций. Для решения системы уравнений удобен прием, основанный на использовании функции напряжений φ(х,у), подобранной таким образом чтобы выполнялись условия 

 . Уравнение равновесия пологой оболочки
. Уравнение равновесия пологой оболочки  .Т.к. направление осей координатсовпадает с направлениями главных кривизн, в этом случае уравнение равновес примет вид
.Т.к. направление осей координатсовпадает с направлениями главных кривизн, в этом случае уравнение равновес примет вид  .где k - кривизны срединной поверхности оболочки.
.где k - кривизны срединной поверхности оболочки.  Обозначим kx/ky=µk, тогда уравнение примет вид
Обозначим kx/ky=µk, тогда уравнение примет вид  . Уравнение решается методом коллокаций. Коллокация - это удовлетворение определенным условиям в отдельных точках оболочки. Процесс решения задачи данным методом состоит в следующем. После выбора функции φ, она подставляется в уравнение равновесия. В области оболочки выбираются точки характерные для очертания эпюр. Ординаты этих точек поочередно подставляются в полученные выражения, в результате чего получается система линейных уравнений. После этого можно вычислить усилия N, в любой точке оболочки. Главные растягивающие и сжимающие усилия и углы наклона оболочек к оси х определяются
. Уравнение решается методом коллокаций. Коллокация - это удовлетворение определенным условиям в отдельных точках оболочки. Процесс решения задачи данным методом состоит в следующем. После выбора функции φ, она подставляется в уравнение равновесия. В области оболочки выбираются точки характерные для очертания эпюр. Ординаты этих точек поочередно подставляются в полученные выражения, в результате чего получается система линейных уравнений. После этого можно вычислить усилия N, в любой точке оболочки. Главные растягивающие и сжимающие усилия и углы наклона оболочек к оси х определяются  ,
,  . Главные растягивающие напр полностью передаются на арм в том
. Главные растягивающие напр полностью передаются на арм в том  случает, если они больше Rbt. Устойчивость обесп при соблюдении условия
случает, если они больше Rbt. Устойчивость обесп при соблюдении условия  гдеEbl=0,2Eb. h-толщина обол. Для воприятия сдвиг усилий между панелями устраивается шпоночный шов, прочность которого проверяется на смтие и на срез. При этом должны выполняться условия
гдеEbl=0,2Eb. h-толщина обол. Для воприятия сдвиг усилий между панелями устраивается шпоночный шов, прочность которого проверяется на смтие и на срез. При этом должны выполняться условия  ,
,  . Sш-расчетное сдвигающее усилие на шпонку. S-расч сдвиг усил на единицу длины, Сш-ширина шпонки, bш-ширина шпонки, δш-глубина шпонки, k-опытный коэф, равный 2 рпи необжатых и 4 при обжатых шпонках.
. Sш-расчетное сдвигающее усилие на шпонку. S-расч сдвиг усил на единицу длины, Сш-ширина шпонки, bш-ширина шпонки, δш-глубина шпонки, k-опытный коэф, равный 2 рпи необжатых и 4 при обжатых шпонках.
