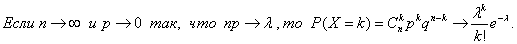Формула полной вероятности и формула Байеса.

Формула полной вероятности Пусть событие А может появиться вместе с одним из образующих полную группу попарнонесовместных событий Н₁,Н₂…Н_n называемых гипотезами, тогда вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на вероятность события А при этой гипотезе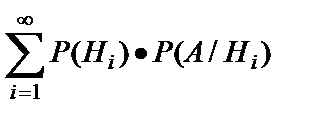

Формула Бейса Пусть имеется полная группа попарнонесовместных гипотез Н₁,Н₂…Н_n с известными вероятностями появления. В результате проведения опыта появилось некоторое события А, требуется переоценить вероятности гипотез при условии, что событие А произошло

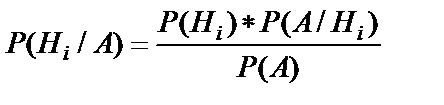
9. Повторные независимые испытания. Формула Бернулли.

Рассмотрим случай многократного повторения одного и того же испытания или
случайного эксперимента. Результат каждого испытания будем считать не зависящим
от того, какой результат наступил в предыдущих испытаниях. В качестве результатов
или элементарных исходов каждого отдельного испытания будем различать лишь две
возможности:
1) появление некоторого события А;
2) появление события 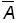, (события, являющегося дополнением А)
Пусть вероятность P(A) появления события А постоянна и равна p (0<.p<1).
Вероятность P( 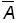) события 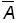обозначим через q: P( 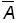) = 1- p=q.

формула Бернулли. Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют "независимыми относительно события А"(Событие А имеет одну и ту же вероятность) "Сложное событие"- совмещение нескольких отдельных событий, которые называют "простыми". Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Теорема.Если производится n независимых опытов в каждом из которых событие А появляется с одинаковой вероятностью р, причем то тогда вероятность того, что событие А появится ровно m раз определяется по формуле.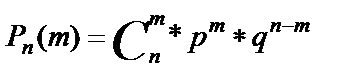

формула Бернули применяется в тех случаях, когда число опытов невелико, а вероятности появления достаточно велики.

10.Полиномиальное распределение является расширением биномиального, поэтому для описания его существа используется аналогичная математическая модель.

Схема независимых испытаний. Пусть в результате испытания может появиться одно из событий A₁, ..., A_n, составляющих исчерпывающее множество событий. Вероятность появления события A_i равна P{A_i} = p_i. Поскольку множество событий исчерпывающее, то p_i + ... + p_m = 1.
Пусть проводится n независимых испытаний.
Тогда числа X₁, ..., X_n появления событий A₁, ..., A_n в серии из n испытаний подчинены полиномиальному закону распределения.
Так как при каждом испытании обязательно появляется одно из событий A₁, ..., A_n, то X₁ + ... + X_n = n.

Извлечение с возвращением. Пусть в множестве из N элементов содержится k₁ элементов с признаком B₁, ..., , k_m элементов с признаком B_m, причем k₁ + ... + k_m = N. Вероятность того, что при случайном выборе одного из элементов множества будет выбран элемент с признаком B_i равна .

Ki/n
Пусть производится n независимых извлечений элементов из множества, причем после каждого извлечения и опознания элемент возвращается в множество. Пусть, наконец, опыт поставлен так, что вероятности p_i не меняются от извлечения к извлечению.
Тогда числа X₁, ..., X_m извлечений элементов с признаками B₁, ..., B_m соответственно подчинены полиномиальному закону распределения. Так как при каждом извлечении обязательно появляется один из элементов с признаком B₁, ..., B_n, то X₁ + ... + X_n = n.

Область х - 0≤Х≤n , Х- целое.

Параметры - n - целое положительное число (испытаний);

p1, ..., pm - вероятности каждого из испытаний

Плотность(функциявероятности)-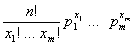

Математическое ожидание-npi

Дисперсия-npi(1 - pi)

Доказательство

Рассмотрим один из возможных случаев, возникший в результате того, что процесс оказался в состояниях A₁, ..., A_m соответственно x₁, ..., x_m раз. Вероятность этого конкретного случая равна 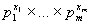. Однако процесс может оказаться в состояниях A₁, ..., A_m соответственно x₁, ..., x_m раз несколькими способами. Число таких конкретных способов будет равно 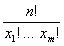. Из этого следует, что вероятность возникновения любого из этих конкретных состояний, при которых процесс может оказаться в состояниях A₁, ..., A_mсоответственно x₁, ..., x_m раз равна 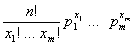. Конечная формула совпадает с формулой плотности полиномиального распределения.

Теорема Пуассона.

Теорема Пуассона: Между биномиальным распределением и распределением Пуассона имеется следующая связь: Пусть n ® µ, p ® 0 и при этом np º a = const. Тогда:

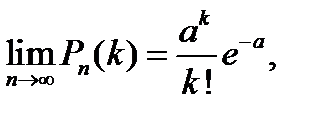
Где .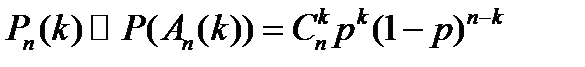

Доказывается эта теорема с использованием второго замечательного предела (1-a/n)ⁿ ® e^-a при n ® µ.

Дискретная СВ Х с реализациями xk = k, k = 0, 1, …, имеет распределение Пуассона с параметром a > 0, что символически записывается как Х ~ П(а), если

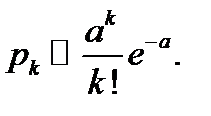
M[X] = D[X] = a.

Эта теоре­ма дает пуассоновское приближение биномиального распределения и обычно используется при p<0,1 и npq 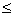9