Определите геометрический смысл определенного интеграла. Поясните, как вычисляется площадь плоской фигуры в прямоугольной декартовой системе координат. Запишите соответствующие формулы

Геометрический смысл определённого интеграла: Определённый интеграл от непрерывной неотрицательной функции численно равен площади криволинейной трапеции ограниченной её графиком.

1.Геометрический смысл определенного интеграла. Если f(x) непрерывна и положительна на [a,b], то интеграл b(в)a(н)f(x)dx представляет собой площадь криволинейной трапеции, ограниченной линиями y=0,x=a,x=b,y=f(x)
2.площадь плоской фигуры в прямоугольной декартовой системе координат -по формуле
S=ин.d(в)c(н) q1(y)-q2(y) dy

Ф-ла ньютона-лейбница:

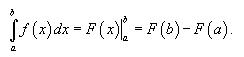
Формула определённого интеграла:

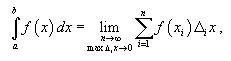
Криволинейная трапеция это фигура ограниченная графиком непрерывной, неотрицательной функции y=f(x) отрезками прямых x=a, x=b

X э [a;b]

Дельта xi=xi+1-xi

Si=дельта xi*mi

Si=дельта xi*Mi

Si= дельта xi*f(Ci)

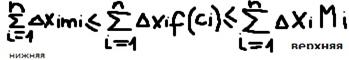
Будем рассматривать всевозможные разбиения отрезка АВ при условии что n стремится к бесконечности , а max дельта xi cтремится к 0.

БИЛЕТ

Для каких вычислений применяется определенный интеграл в геометрии? Запишите и поясните формулы для вычисления объема тела по известным площадям его поперечных сечений и для объема тела вращения.

определ.инт.в геометрии
1. определенный интеграл применяется в геометрии для геометрических и физических вычислений
2. Получите формулу для вычисления объема тела по известным площадям его поперечных сечений и для объема тела вращения.
1) S=ин.b(в)a(н) S(x)dx
2) V=П*ин.b(в)a(н) (f(ф))2(кв)*dx следует S=2П|ин.b(в)a(н) f(x)*(корень) 1+(f'(x))2*dx

БИЛЕТ

Определите понятие несобственного интеграла I рода, сформулируйте его свойства. Запишите формулы Ньютона-Лейбница и объясните процесс вычисления по ней несобственных интегралов.

Пусть функция y=f(x) непрерывна при любом x≥0. Рассмотрим интеграл с неопределённым верхним пределом “I(b) = ^b∫_a f(x)dx”

Предположим, что при b→+∞ функция имеет конечный предел то этот предел называеться сходящийся несобственным интегралом от функции f(x) по промежутку [a,+∞) и обозначается как: ^+∞∫­_a f(x)dx = lim_b→∞ ^b∫_a f(x) dx.

Если предел не существует или = бесконечности, то несобственный интеграл называется расходящемся.

Геометрически несобственный интеграл от неотрицательной функции выражает площадь криволинейной трапеции, ограниченной сверху графиком функции y=f(x), слева – отрезком прямой x=a, снизу осью Ох.

Эта площадь является конечной, в случае расходящейся – бесконечной.

^+∞∫­_a f(x)dx = lim_b→∞ ^b∫_a f(x) dx = lim_b→∞ (f(b) – f(a)) = f(+∞) – f(a), где f(+∞)=lim_b→+∞ f(b).

Аналогично определяется несобственный интеграл с бесконечным нижним пределом:

^b∫­_-∞ f(x)dx = lim_b→-∞ ^b∫_a f(x) dx.

И несобственный интеграл с общим бесконечным пределом ^+∞∫_-∞f(x)dx=^c∫_-∞f(x)dx+^+∞∫_c f(x)dx

Где с – любая точка из интеграла (-∞, +∞).

Если три x≥a выполнены неравенства 0≤ⱷ≤f(x) и ^+∞∫_c f(x)dx сходиться , то сходится и ^+∞∫_c ⱷ (x)dx, причём ^+∞∫_c ⱷ (x)dx ≤ ^+∞∫_c f(x)dx если ^+∞∫_c ⱷ (x)dx расходиться, то расходиться и ^+∞∫_c f(x)dx.
Если в промежутке (а, +∞) функция f(x) изменяет знак и ^+∞∫_c |f(x)|dx сходиться, то сходиться также и ^+∞∫_c f(x)dx

БИЛЕТ

Дать определение обыкновенного дифференциального уравнения, его порядка, общего и частного решения. Сформулировать теорему о существовании и единственности решения дифференциального уравнения. Сформулировать задачу Коши для ДУ высших порядков.

Дифференциальные уравнения – уравнения, которые связывают между собой независимую переменную Х и искомую функцию Y и её производные различных порядков по переменной Х.

Порядок дифф.ур.-порядок старшей производной в данном ур. (y⁴-y³-e^x=0 – 4 порядок).

Общее решение дифф.ур. – y=µ (X,C₁,C₂,…,C_N), которое содержит столько произвольных постоянных каков порядок ур.

Всякое решение, которое получается из общего при конкретных значений произвольных постоянных – частное решение. Для нахождения частного решения требуется задать дополнительные условия – условия Коши.

Теорема о существовании и единственности решения ду: Пусть функция f(x, y, p₁, p₂, …,p_n-1) непрерывна и имеет непрерывные частные производные в некоторой области D и пусть точка (x₀, y₀, y₁, y₂, …, y_n-1) принадлежит области D. Тогда в некоторой окрестности точки x₀ существует решение уравнения , удовлетворяющее начальным условиям . Это решение единственно.

Коши для ДУ высших порядков: уравнение вида F(x, y, y', y'', ..., y⁽ⁿ⁾) = 0,
где F - известная функция (n+2) переменных, определенная в области D, x - независимая переменная из интервала (a, b), y = y(x) - неизвестная функция, n - порядок уравнения.

БИЛЕТ

Дать определения дифференциального уравнения первого порядка, его общего и частного решения. Сформулировать задачу Коши для ДУ-1. Записать дифференциальное уравнение с разделяющимися переменными. Объясните способ его решения.

дифференциальнным уравнения 1-го порядка и формула..так называется уравнение которое связывают между собой независимую переменную Х , и искомую функцию У , и ее производные различных порядков по переменной Х.
F(x,y,y'...y(ст.n))=0 -неявная ф-ия
y(ст.n))=f(x,y,y'...y(ст.n-1))) - нормальная ф-ия
2.1.общего решения ДУ-1 – наз. такое уравнение : y=ф(x,c1,c2...c(ст.n)) которое содержит столько производных постоянных каков порядок самого уравнения.
2.2.Всякое реш.д.у. которое получ.из общего реш.при конкретных знач.произвольных постоянных назыв.частными.
2.3.Сформулируйте задачу Коши для ДУ-1:
y(x0)=y0
y'(x0)=y'0
y(ст.n-1)(x0)=y0(ст.n-1)
Задачу Коши для ДУ-1 – для нахождения частного решения необходимо задание дополнительных условий .

БИЛЕТ