Метод Леонтьева многоотраслевой экономики.

Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из отраслей, чтобы удовлетворить все потребности в продукции этой отрасли. При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой – как потребитель продукции и своей, и произведенной другими отраслями. Математическая модель Леонтьева позволяет анализировать связь между отраслями.

Задача.

В таблице приведены данные об использовании стоимостного баланса за отчетный период, усл. ден. ед.:

№ п/п	Отрасль	Потребление	Конечный продукт	Валовый продукт
Q1	Q2
	Q1
	Q2

Требуется:

1) составить матрицу прямых затрат и проверить ее продуктивность;

2) вычислить объемы конечного продукта при увеличении валового выпуска каждой отрасли соответственно на 100% и 50%;

3) Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление отрасли Q1 увеличить в k = 1 раз, а отрасли
Q2 – на 10%.

Решение: 1. Введем в рассмотрение матрицу 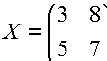и векторы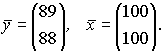

Составим матрицу прямых затрат А, учитывая, что ее элементы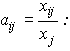

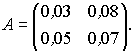
Легко видеть, что сумма элементов столбцов (строк) А меньше единицы. Следовательно, в силу второго критерия продуктивности (матрица продуктивна, если максимум сумм элементов её столбцов не превосходит единицы) матрица А продуктивна.

2. Уравнение линейного межотраслевого баланса имеет вид:

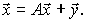
При увеличении валового выпуска отраслей Q1 и Q2 соответственно на 100% и 50% получим новый вектор валового выпуска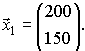

Вектор потребления 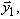соответствующий вектору 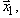найдем из уравнения баланса:

.

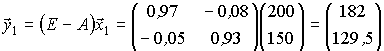Изменения объемов конечного продукта Q1 на 182 – 89 = 93 ед. или 104,5%, Q2 – на 129,5 – 98 = 41,5 ед. на 47,2%.

3. Конечное потребление отрасли Q1 остается без изменения, а отрасли Q2 станет равным Получим новый вектор потребления

.

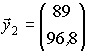Новый вектор валового выпуска найдем из уравнения баланса

.

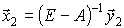Обратная матрица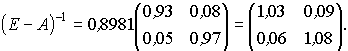

Откуда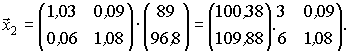

Валовый продукт отраслей необходимо увеличить Q1 на 0,38%, Q2 – на 9,88%.

Собственные значения и собственные векторы матрицы.

Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A, если

Av = λv,

где число λ называется собственным значением матрицы A. Таким образом преобразование, которое выполняет матрица A над вектором v, сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и αv — тоже собственный вектор.

Собственные значения

У матрицы A , размерностью (N×N) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению

det(A − λI) = 0,

являющемуся алгебраическим уравнением N-го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

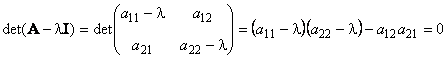
Например,

Рис. 21 Собственные значения

Набор собственных значений λ1,..., λN матрицы A называется спектром A.

Спектр обладает разнообразными свойствами. В частности

det(A) = λ1×...×λN, Sp(A) = λ1+...+λN.

Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная (At = A), то ее собственные значения вещественны.

Собственные векторы

У матрицы A, размерностью (N×N) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора vn нужно решить систему однородных уравнений

(A − λnI) vn = 0.

Она имеет нетривиальное решение, поскольку det(A − λnI) = 0.

Например,

Рис. 22 Собственные вектора

Собственные вектора симметричной матрицы ортогональны.