Канонические уравнения эллипса, гиперболы, параболы и окружности.

Окружностью называется геометрическое место точек, равноудаленных от точки, называемой центром окружности (рис. 6).

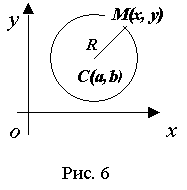
Пусть центр окружности находится в точке С(а, b). Т.к. окружность есть множество точек М(х, у), находящихся на расстоянии R (радиус окружности) от центра С(а, b), то 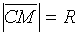, то есть

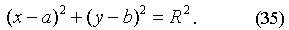
Уравнение (35) и есть уравнение окружности с центром в точке С(а, b) и радиусом R.

Эллипс есть геометрическое место точек, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (большая, чем расстояние между фокусами).

Внешний вид уравнения какого-либо геометрического места точек зависит от взаимного расположения этого множества точек и декартовой системы координат.

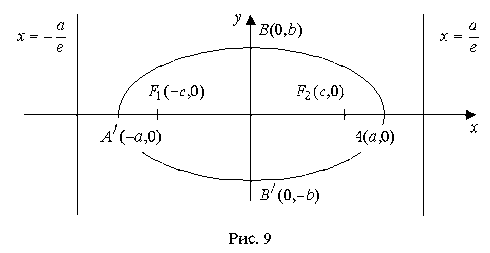
Выберем прямоугольную систему декартовых координат так, чтобы ось абсцисс проходила через оба фокуса F1 и F2, начало координат находится в середине отрезка F1F2 (рис. 7). Если обозначить расстояние между фокусами F1 и F2 через 2с, тогда координаты фокусов будут соответственно (-с, 0) и (с, 0).

Пусть М(х, у) - текущая точка эллипса (рис. 7).

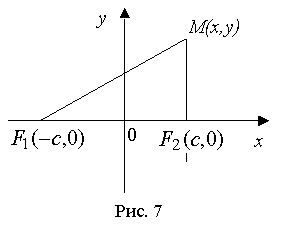
Обозначим сумму расстояний F1M и F2M через 2а (a > c по правилу треугольника), т.е. 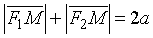, или

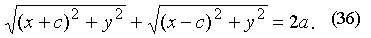
Уравнение (36) и есть уравнение эллипса. Приведем его к более простой для исследований форме:

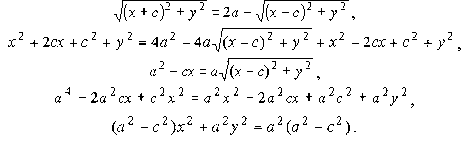
Поскольку a > c, то можно обозначить

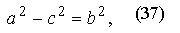
тогда получаем

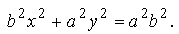
Окончательно получим (при выбранной системе координат) уравнение

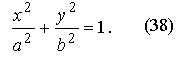
Уравнение (38) называют каноническим уравнением эллипса.

Замечание. Т.к. в процессе преобразований дважды возводились в квадрат обе части уравнения, то необходимо проверить, не получены ли "лишние" точки. Для этого нужно показать, что если координаты произвольной точки M0(x0, y0) удовлетворяют уравнению (38), то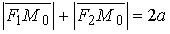

Эта задача предлагается студентам для самостоятельного решения.

Сделаем некоторые замечания о форме эллипса. Из уравнения (38) понятно, что оси координат Ох и Оу являются осями симметрии эллипса и, следовательно, начало координат является центром симметрии эллипса.

Рассмотрим часть эллипса, расположенную в первой четверти, для которой можем записать уравнение (38) в виде:

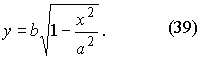
Отсюда видно, что если x = 0, то y = b и, далее, с ростом х значения у убывают. Когда x = a, то y = 0 (рис. 8).

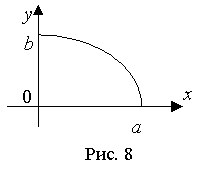
Числа а и b называют полуосями эллипса.

Учитывая симметрию эллипса относительно осей координат, можем построить полный эллипс (рис. 9).

Если изменяется величина с, то меняется форма эллипса, а именно: если 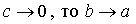и при c = 0 эллипс становится окружностью с уравнением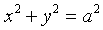

Т.о., окружность есть частный случай эллипса, когда полуоси эллипса равны между собой. Если же 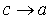, то 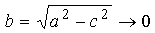, т.е. эллипс сжимается вдоль оси Оу.
Величина 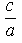может служить числовой характеристикой сжатия эллипса.
Число 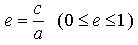называют эксцентриситетом эллипса.
Две прямые 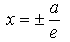называются директрисами эллипса.
Точки пересечения эллипса с осями симметрии называют вершинами эллипса.

Гипербола есть геометрическое место точек, абсолютное значение разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами).

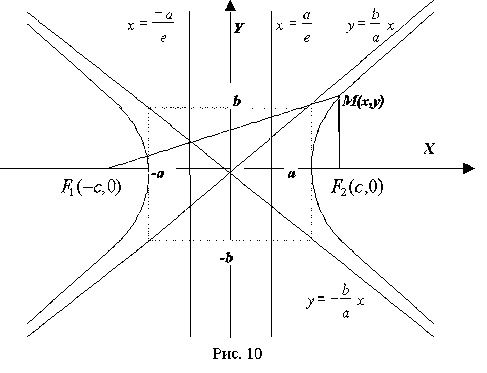
Расстояние между фокусами F1 и F1 обозначим 2c. Систему координат выберем так же, как при выводе уравнения эллипса (рис. 10).

Из определения имеем

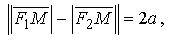
следовательно, a > c. Опуская вывод, запишем уравнение гиперболы

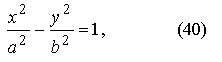
где b2 =c2- a2.

Уравнение (40) называют каноническим уравнением гиперболы. Число а называют действительной полуосью гиперболы, число b - мнимой полуосью.

Отметим, что согласно уравнению (40) гипербола симметрична относительно осей координат и, следовательно, относительно начала координат. Т.к. из канонического уравнения гиперболы следует, что

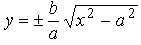
то нет точек кривой в полосе -a > x > a.

Кривая состоит из двух отдельных частей - ветвей гиперболы, лежащих в областях 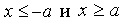(рис. 10).

Можно показать, что при 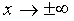ветви гиперболы неограниченно приближаются к прямым 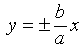, не пересекая этих прямых.

Эти две прямые называются асимптотами гиперболы (рис. 10).
Число 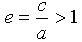, количественно характеризующее сжатие ветвей гиперболы, называют эксцентриситетом гиперболы.
Точки пересечения гиперболы с действительной осью называются вершинами гиперболы.
Две прямые 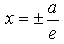называют директрисами гиперболы.

Директрисы гиперболы параллельны оси Оу и пересекают ось Ох между вершинами гиперболы.

Парабола есть геометрическое место точек, для каждой из которых расстояние от некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой (директриса не проходит через фокус).

Выберем систему координат так, чтобы ось абсцисс проходила через точку фокуса F перпендикулярно директрисе L, начало координат расположим в середине отрезка FN (рис. 11).

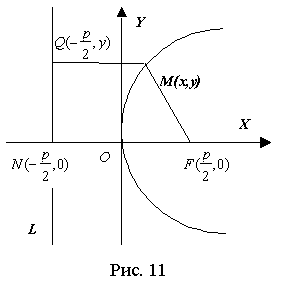
Расстояние между фокусом F и директрисой L обозначим р. Значение р называют параметром параболы.

Пусть M(x, y) - текущая точка параболы, тогда, по определению параболы имеем 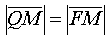или 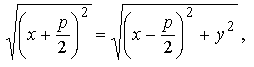отсюда получаем

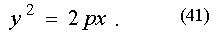
Уравнение (41) называют каноническим уравнением параболы.

Вершина параболы находится в начале координат, и кривая симметрична относительно оси Ох (рис. 11).

Замечание. Если для эллипса и гиперболы обозначим через r расстояние от текущей точки кривой до какого-либо фокуса, а через d - расстояние от этой точки до односторонней с этим фокусом директрисы, то оказывается, что

Для параболы же 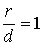, что следует из ее определения.

Т.о., для рассмотренных кривых второго порядка эллипса, гиперболы, параболы имеет место фокально-директориальное свойство: отношение расстояния текущей точки кривой до фокуса к расстоянию до односторонней с этим фокусом директрисы равно эксцентриситету кривой, т.е.

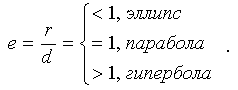
Канонические уравнения (38), (40), (41) эллипса, гиперболы, параболы получены при специальном выборе начала координат и направления осей координат, поэтому они просты и удобны для анализа. Оказывается, что в общем случае уравнения этих кривых представляют собой уравнения типа (34). Но эти уравнения всегда можно привести к каноническому виду, осуществляя преобразования системы координат.

Определители. Их свойства.

Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица.

Определитель второго порядка вычислим, например, по элементам первой строки

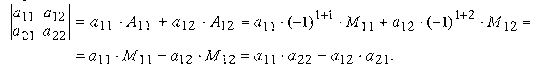
Запишем разложение данного определителя по элементам второй строки

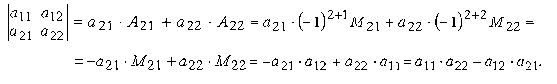
Полученный результат совпадает с результатом вычисления определителя по первой строке. Этот же результат получится и при разложении по любому из столбцов. Рекомендуем это проверить самостоятельно.

Из сказанного можно заключить, что определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.

Пример. .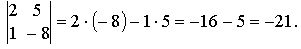

Найдем определитель третьего порядка, раскладывая его по элементам, например, третьего столбца

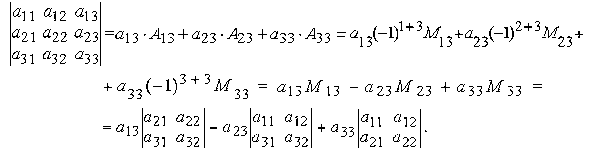
Пример.

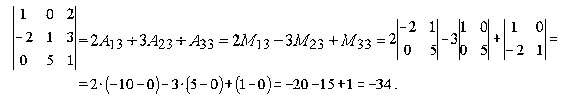
Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Получается, что определитель n - го порядка мы найдем через определители (n -1) - го порядка.

Перечисленные ниже свойства рекомендуется использовать при вычислении определителей.

1. Общий множитель любой строки (столбца) можно выносить за знак определителя.
2. Если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то величина определителя не изменится.
3. Если в определителе есть нулевая строка (столбец), то определитель равен нулю.
4. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
5. Определитель с двумя одинаковыми строками (столбцами) равен нулю.