Вопрос 1.Множества и действия с ними

Вопрос 1.Множества и действия с ними

Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.

Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.

Если элемент x принадлежит множеству X, то записываютx∈Х (∈ — принадлежит).
Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).

Основные числовые множества

N	{1,2,3,...,n} Множество всех натуральных чисел
Z	{0, ±1, ±2, ±3,...} Множество целых чисел.Множество целых чисел включает в себя множество натуральных.

Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается Ø.

Элементы логической символики

→	"следует", "выполняется"
↔	равносильность утверждения
:	"такой, что"

:При записи математических выражений часто используются кванторы.

Квантором называется логический символ, который характеризует следующие за ним элементы в количественном отношении.

• ∀- квантор общности, используется вместо слов "для всех", "для любого".
• ∃- квантор существования, используется вместо слов "существует", "имеется". Используется также сочетание символов ∃!, которое читается как существует единственный.

Операции над множествами

Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.
Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.

Объединением (суммой)множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}

Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}

Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}

Свойства операций над множествами

Свойства перестановочности

A ∪ B = B ∪ A
A ∩ B = B ∩ A

Сочетательное свойство

(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)

Счетные и несчетные множества

Для того, чтобы сравнить два каких-либо множества А и В, между их элементами устанавливают соответствие.

Если это соответствие взаимооднозначное, то множества называются эквивалентными или равномощными, А В или В А.

Пример 1

Множество точек катета ВС и гипотенузы АС треугольника АВС являются равномощными.

Отношения множеств.

Когда говорят о родстве двух человек, Маша и Саша, то подразумевают, что есть некая семья, к членам которой они относятся. Упорядоченная пара (Маша, Саша) отличается от других упорядоченных пар людей тем, что между Машей и Сашей есть некое родство (кузина, отец, и т. д.). В математике среди всех упоря­доченных пар декартового произведения А´В двух множеств А и В тоже выделяются некоторые пары в связи с тем, что между их компонентами есть некоторые «родственные» отношения, которых нет у других.

В качестве примера рассмотрим множество S студентов какого-нибудь техникума и множество D изучаемых там дисциплин. В декартовом произведении S´D можно выделить большое подмножество упорядоченных пар (s, d),обладающих свойством: студент s изучает дисциплину d. Построенное подмножество отражает отношение «изучает», естественно возникающее между множествами студентов и дисциплин.

Для строгого математического описания любых связей между элементами двух множеств вводится понятие бинарного отноше­ния, которое часто появляется как в ма­тематике, так и в информатике. Отношением (бинарным отношением, двуместным отношением) из множества A в множество B называется некоторое подмножество декартового произведения , Отношения в дальнейшем будем обозначать , (читается отношение из A в B)

Если , и , то говорят, что a находится в отношении с b. Используется также запись
ПРИМЕР :
Если отношение из A в A ( ), то говорят бинарное отношение на множестве A.

ПРИМЕР

Сложение комплексных чисел

Пример 1
Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Для комплексных чисел справедливо правило первого класса: – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность:

Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел ,

Очевидно, что произведение следует записать так:

Все алгебраические действия вам знакомы, главное, помнить, что и быть внимательным.

Надеюсь, всем было понятно, что

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, что и не путаемся в знаках!!!).

Распишу подробно:

Пример я подобрал «хороший», если взять два числа «от балды», то в результат деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5 Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :

, .Тригонометрическая и показательная форма комплексного числа

Любое комплексное число (кроме нуля) можно записать в тригонометрической форме:
, где – это модуль комплексного числа, а – аргумент комплексного числа..

Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что :

Модулем комплексного числа называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.

Модуль комплексного числа стандартно обозначают: или

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедлива для любых значений «а» и «бэ».

Примечание: модуль комплексного числа представляет собой обобщение понятия модуля действительного числа, как расстояния от точки до начала координат.

Аргументом комплексного числа называется угол между положительной полуосью действительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .

Аргумент комплексного числа стандартно обозначают: или

Из геометрических соображений получается следующая формула для нахождения аргумента:
. Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-й и не 4-й координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.

Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.

Пример 7

Представить в тригонометрической форме комплексные числа: , , , .
Выполним чертёж:

На самом деле задание устное. Для наглядности перепишу тригонометрическую форму комплексного числа:

Запомним намертво, модуль – длина (которая всегда неотрицательна), аргумент – угол.

1) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что . Формальный расчет по формуле: .
Очевидно, что (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме: .

Ясно, как день, обратное проверочное действие:

2) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что . Формальный расчет по формуле: .
Очевидно, что (или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме: .

Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):

3) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что . Формальный расчет по формуле: .
Очевидно, что (или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме: .

Проверка:

4) И четвёртый интересный случай. Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что . Формальный расчет по формуле: .

Аргумент можно записать двумя способами: Первый способ: (270 градусов), и, соответственно: . Проверка:

Однако более стандартно следующее правило: Если угол больше 180 градусов, то его записывают со знаком минус и противоположной ориентацией («прокруткой») угла: (минус 90 градусов), на чертеже угол отмечен зеленым цветом. Легко заметить, что и – это один и тот же угол.

Таким образом, запись принимает вид:

Внимание! Ни в коем случае нельзя использовать четность косинуса, нечетность синуса и проводить дальнейшее «упрощение» записи:

В оформлении простейших примеров так и следует записывать: «очевидно, что модуль равен… очевидно, что аргумент равен...». Это действительно очевидно и легко решается устно.

,Возведение комплексных чисел в степень

формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень справедлива формула:

Как умножить матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

Пример:

Умножить матрицу 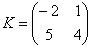на матрицу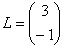
Я буду сразу приводить формулу для каждого случая:

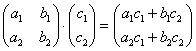– попытайтесь сразу уловить закономерность.

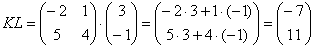
Пример сложнее:

Умножить матрицу 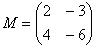на матрицу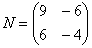

Формула: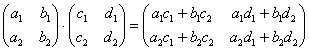

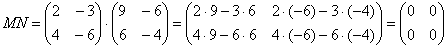
В результате получена так называемая нулевая матрица.

Попробуйте самостоятельно выполнить умножение 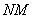(правильный ответ ).

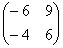Обратите внимание, что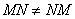 ! Это почти всегда так!

Таким образом, при умножении переставлять матрицы нельзя!

Если в задании предложено умножить матрицу 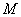на матрицу 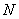, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Вопрос преобразований. 8Нахождение обратной матрицы с помощью элементарных преоразований

Вопрос10.Ранг матрицы.

Рангом системы строк называется максимальное число линейно независимых строк этой системы.

Прямая линия на плоскости.

Прямая –это геометрическое место точек, удовлетворяющих общему уравнению на плоскости :

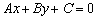Вектор, который параллелен прямой, называется направляющим вектором данной прямой. Очевидно, что у любой прямой бесконечно много направляющих векторов, причём все они будут коллинеарны (сонаправлены или нет – не важно).

Направляющий вектор обозначают следующим образом: .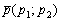

Но одного вектора недостаточно для построения прямой, вектор является свободным и не привязан к какой-либо точке плоскости. Поэтому дополнительно необходимо знать некоторую точку 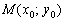, которая принадлежит прямой.Как составить уравнение прямой по точке и направляющему вектору?

Если известна некоторая точка 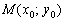, принадлежащая прямой, и направляющий вектор 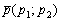этой прямой, то уравнение данной прямой можно составить по формуле:

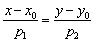
Уравнение прямой 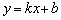называется уравнением прямой с угловым коэффициентом 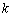. Например, если прямая задана уравнением 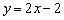, то её угловой коэффициент: 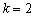. Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:

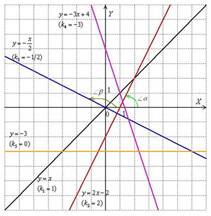
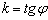
В курсе геометрии доказывается, что угловой коэффициент прямой равен тангенсу угла между положительным направлением оси и данной прямой: 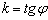, причём угол 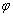«откручивается» против часовой стрелки.

угловой коэффициент характеризует степень наклона прямой к оси абсцисс.

Вопрос 16, Парабола

Параболой называется множество всех точек плоскости, равноудалённых от данной точки и данной прямой , не проходящей через точку .

Точка называется фокусом параболы, прямая – директрисой (пишется с одной «эс») параболы. Константа «пэ» канонического уравнения называется фокальным параметром, который равен расстоянию от фокуса до директрисы. . При этом фокус имеет координаты , а директриса задаётся уравнением .

Вопрос 17.Числовая последовательность и ее предел. Числовой последовательностью называется бесконечное множество чисел

(1)

следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого задается как функция целочисленного аргумента, т.е. .

Число А называется пределом последовательности (1), если для любого существует число , такое, что при выполняется неравенство . Если число А есть предел последовательности (1), то пишут

Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.

Для сходящихся последовательностей имеют место теоремы:

если .

Вопрос 1 8.Предел функции в точке. Число А называется пределом функции в точке х_о (или при х→х_о), если для любого положительного ε найдется такое положительное число δ, что для все х¹х_о, удовлетворяющих неравенству |х-х_о|<δ, выполняется неравенство |ƒ(х)-А|<ε.

Вопрос 19.Свойства пределов..

.

Теорема 6. предел произведения равен произведению пределов.

.

Следствие. Постоянный множитель можно выносить за знак предела.

.

Теорема 7. Если функции f(x) и g(x) имеют предел при ,

причем , то и их частное имеет предел при , причем предел частного равен частному пределов.

, .

Вопрос 20.Неопределенности в пределах.

Неопределенности - выраженийя значение которых не определено. основные виды неопределенностей: ноль делить на ноль (0 на 0), бесконечность делить на бесконечность , ноль умножить на бесконечность , бесконечность минус бесконечность , единица в степени бесконечность , ноль в степени ноль , бесконечность в степени ноль .

Вопрос 21. Бесконечно большая величина. Не существует такого понятия как «просто бесконечно малая функция» или «просто бесконечно большая функция». Функция может быть бесконечно малой или бесконечно большой только в конкретной точке. Начертим линию :

Данная функция бесконечно малА в единственной точке:
В точках «плюс бесконечность» и «минус бесконечность» эта же функция будет уже бесконечно большой: . Или в более компактной записи:

Вопрос 24. Таблица производных

Вопрос 1.Множества и действия с ними

Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.

Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.

Если элемент x принадлежит множеству X, то записываютx∈Х (∈ — принадлежит).
Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).

Основные числовые множества

N	{1,2,3,...,n} Множество всех натуральных чисел
Z	{0, ±1, ±2, ±3,...} Множество целых чисел.Множество целых чисел включает в себя множество натуральных.

Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается Ø.