Произвольная система линейных уравнений

Вернемся к произвольной системе линейных уравнений вида ( 4.1 ).

Утверждение 4.1.Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда (числу неизвестных).

Утверждение 4.2.Система линейных уравнений неопределенна тогда и только тогда, когда .

Нахождение решения для таких систем можно описать следующим алгоритмом:

1. Находим ранги основной и расширенной матриц системы. Если они не равны, то по теореме Кронекера-Капелли система несовместна.

2. Если ранги равны, то выделяем базисный минор. При этом, неизвестные, коэффициенты при которых вошли в базисный минор, составят группу зависимых переменных, остальные – группу независимых (вообще говоря, выбор зависимых и независимых неизвестных может быть неоднозначным).

3. Вычеркиваем те уравнения системы, коэффициенты которых не вошли в состав базисного минора (их можно получить из него).

4. Члены уравнений, содержащие свободные неизвестные, переносятся в правую часть (для матрицы – это означает изменение знака соответствующего коэффициента). В результате получится система из 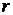уравнений, содержащая 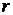неизвестных, причем ее определитель отличен от нуля.

5. Решая полученную систему одним из способов, предложенных выше, получаем общее решение системы, в котором зависимые неизвестные будут выражены через свободные.

6. Если известны некоторые значения свободных переменных, то, подставляя их в общее решение, можно получить одно из частных решений системы.

Пример 4.14.Исследовать совместность и найти общее решение и одно из частных решений системы линейных уравнений:

.

Решение. Выпишем основную и расширенную матрицы системы, пометив сверху столбцы соответствующими неизвестными. Если мы найдем ранг расширенной матрицы, то тем самым найдем и ранг основной матрицы. Переставим 4-ый столбец перед первым, при этом система уравнений не изменится.

.

Приведем матрицу к треугольному виду. Напомним, что преобразования можно осуществлять только со строками. Умножим первую строку на (-2) и сложим со второй строкой. Умножим первую строку на (-7) и сложим с третьей строкой, при этом первая остается без изменения:

{Вторая и третья строки – пропорциональны, следовательно, можно вычеркнуть, например, третью строку без изменения значения определителя матрицы} /

Найдем наивысший минор, принадлежащий и основной и расширенной матрице: . Возьмем данный минор как базисный. В него вошли коэффициенты при неизвестных 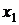и 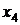– следовательно, это зависимые переменные, а независимыми остались переменные 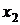и 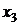. Отсюда можно записать общее решение системы, для чего нужно перенести коэффициенты при свободных переменных в правую часть системы:

;

Для вычисления частного решения зададим значения свободным переменным: , , 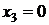откуда , .

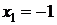Проверка: подставим найденное частное решение в исходную систему:

.

Ответ: общее решение системы: , одно из частных решений: 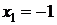, , , .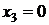