Система линейных уравнений с двумя неизвестными

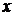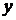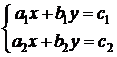Рассмотрим систему линейных уравнений с двумя неизвестными и : , где 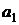, , 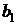, 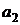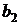– коэффициенты при неизвестных; 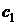, 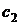– свободные члены.

Как известно из школьного курса, подобные системы решаются методом исключения, например, умножим первое уравнение на 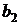, второе на 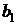и вычтем второе из первого, таким образом, избавляемся от второго неизвестного:

,

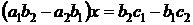(4.2 )

откуда 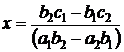. Аналогично определяется и второе неизвестное:

,

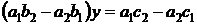( 4.3 )

откуда 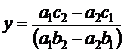. Введем три определителя:

, , .

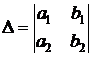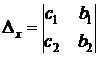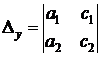Определитель 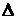составлен из коэффициентов при неизвестных; определитель 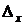получается из 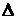заменой первого столбца на столбец свободных членов; определитель 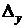– аналогичной заменой второго столбца. Тогда равенства (4.2 ) и ( 4.3 ) можно переписать в виде: 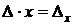, 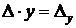. Рассмотрим возможные случаи:

1) 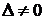. В этом случае система имеет единственное решение:

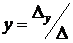и .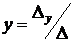

Это решение известно как правило Крамера.

2) 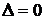. В этом случае имеются две возможности:

а) 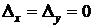и тогда система имеет бесконечное множество решений;

б) 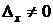или 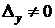, тогда система не имеет решений, так как одно из равенств противоречиво.

Система 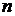линейных уравнений с 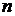неизвестными

Точно так же можно исследовать решение системы, содержащей 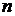линейных уравнений с 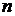неизвестными:

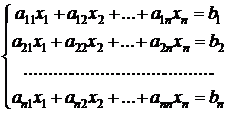
Введем обозначения: неизвестные обозначим вектором 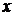; коэффициенты при неизвестных – матрицей 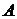; правые части – как вектор :

, ,

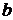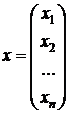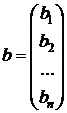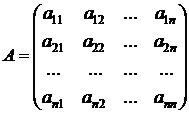
тогда система перепишется в виде: .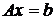

Главнымопределителем этой системы является определитель 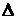матрицы 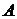: 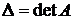. Кроме него можно составить еще 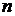определителей по правилу: определитель 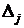получается из определителя 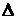заменой 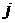-того столбца на столбец 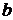правых частей уравнений 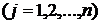. Для системы 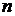-ого порядка справедлив тот же закон, что и для системы двух уравнений.

Правило Крамера

1. Если 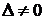, система 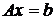имеет единственное решение:

, , …, .

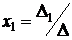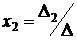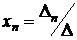( 4.4 )

2. Если 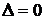, а хотя бы один из определителей 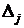, где 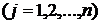, не равен нулю, то система не имеет решений.

3. Если 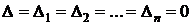, то система имеет бесконечно много решений.

Для системы линейных уравнений, в которой число уравнений равно числу неизвестных, имеет место утверждение: такая система имеет единственное решение тогда и только тогда, когда ее главный определитель отличен от нуля.

Матричный метод

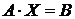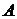Пусть дано матричное уравнение: , где и 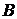- заданные матрицы, причем матрица 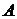– невырожденная. Требуется найти матрицу .

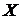Матричный метод решения состоит в следующем: так как матрица 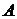– невырожденная, то существует обратная матрица 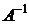. Если умножить слева обе части первого из рассматриваемых уравнений на 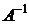: 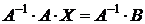, так как 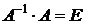, то

.

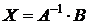( 4.5 )

Аналогично, рассуждаем при поиске решения матричного уравнения вида

.

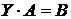Умножаем справа обе части уравнения на матрицу 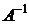, обратную к матрице 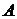, получаем формулу:

.

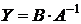( 4.6 )

Метод Гаусса-Жордано

Данный метод еще называют методом исключения неизвестных. Суть его состоит в том, что исходную матрицу преобразуют по строкам так, чтобы обнулить коэффициенты при неизвестных, и привести матрицу к треугольному виду.

Пример 4.12.Решить систему линейных уравнений, используя правило Крамера, матричным методом и методом Гаусса-Жордано:

.

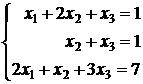Решение (правило Крамера). Согласно правилу Крамера нужно составить определители системы и соответствующие каждому неизвестному. И затем по формуле ( 4.4 ) найти решение.

1. Найдем определитель системы:

.

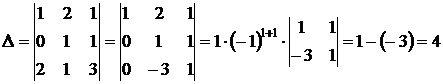2. Найдем определители для каждого неизвестного, заменяя столбец коэффициентов при этом неизвестном, столбцом свободных членов:

;

.

.

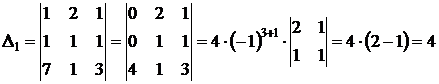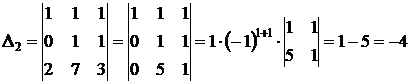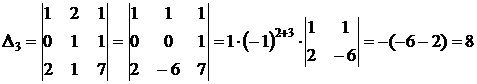3. Теперь по формуле ( 4.4 ) определим значения неизвестных:

; ; .

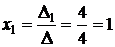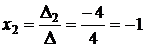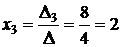Ответ: ; ; .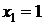

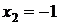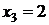Решение (матричным методом):

1. Введем обозначения:

; ; ,

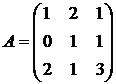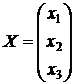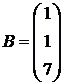тогда исходную систему можно переписать в виде: .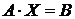

2. Решение такой системы определяется по формуле ( 4.5 ), в которую входит матрица обратная к исходной 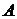. Найдем ее:

2.1 определитель исходной матрицы мы уже находили, он равен: ;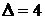

2.2 транспонируем исходную матрицу: ;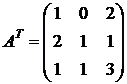

2.3 для каждого элемента транспонированной матрицы нужно найти алгебраические дополнения:

; ; ; ; ; ; ; ; .

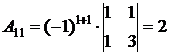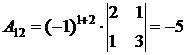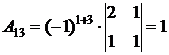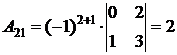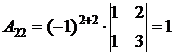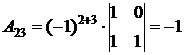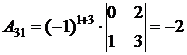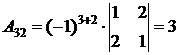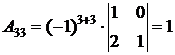2.4 записать их в транспонированную матрицу вместо ее элементов и разделить каждый элемент на определитель исходной матрицы:

.

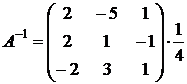3. Подставляем в формулу ( 4.5 ):

.

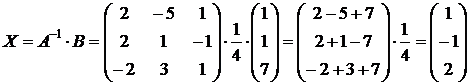Ответ: .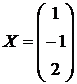

Решение (методом Гаусса-Жордано):

Составляем расширенную матрицу системы и преобразуем к треугольному виду. Умножим элементы первой строки на (-2) и сложим с соответствующими элементами третьей строки. Затем умножим элементы второй строки на 3 и сложим с соответствующими элементами третьей строки:

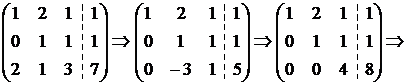
получили треугольную матрицу, которая соответствует системе:

.

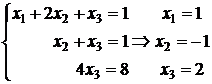Ответ: 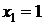; ; .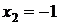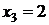