Собственно – случайный отбор
В результате выборочного обследования стажа работы сотрудников предприятия получены данные, сведенные в таблицу:
| Стаж работы (лет) | х1 | х2 | х3 | х4 | х5 | х6 |
| Число работников | m1 | m2 | m3 | m4 | m5 | m6 |
N – общее число сотрудников. Определить:
а) средний стаж работы и среднее квадратическое отклонение;
б) доверительный интервал, в котором с надежностью 0,9973 заключен средний стаж работы сотрудников всего предприятия при повторном и бесповторном отборе;
в) доверительный интервал, в котором с надежностью 0,9545 заключена доля сотрудников предприятия, имеющих стаж работы х4 лет и более при повторном и бесповторном отборе.
| 1. | Стаж работы (лет) | ||||||
| Число работников |
N=2500
| 2. | Стаж работы (лет) | ||||||
| Число работников |
N=1100
| 3. | Стаж работы (лет) | ||||||
| Число работников |
N=1000
| 4. | Стаж работы (лет) | ||||||
| Число работников |
N=2100
| 5. | Стаж работы (лет) | ||||||
| Число работников |
N=1500
| 6. | Стаж работы (лет) | ||||||
| Число работников |
N=1200
| 7. | Стаж работы (лет) | ||||||
| Число работников |
N=2200
| 8. | Стаж работы (лет) | ||||||
| Число работников |
N=2600
| 9. | Стаж работы (лет) | ||||||
| Число работников |
N=2000
| 10. | Стаж работы (лет) | ||||||
| Число работников |
N=2100
| 11. | Стаж работы (лет) | ||||||
| Число работников |
N=5500
| 12. | Стаж работы (лет) | ||||||
| Число работников |
N=1100
| 13. | Стаж работы (лет) | ||||||
| Число работников |
N=2000
| 14. | Стаж работы (лет) | ||||||
| Число работников |
N=1000
| 15. | Стаж работы (лет) | ||||||
| Число работников |
N=2200
| 16. | Стаж работы (лет) | ||||||
| Число работников |
N=2000
| 17. | Стаж работы (лет) | ||||||
| Число работников |
N=1000
| 18. | Стаж работы (лет) | ||||||
| Число работников |
N=2000
| 19. | Стаж работы (лет) | ||||||
| Число работников |
N=2500
| 20. | Стаж работы (лет) | ||||||
| Число работников |
N=1100
| 21. | Стаж работы (лет) | ||||||
| Число работников |
N=1000
| 22. | Стаж работы (лет) | ||||||
| Число работников |
N=2100
| 23. | Стаж работы (лет) | ||||||
| Число работников |
N=1500
| 24. | Стаж работы (лет) | ||||||
| Число работников |
N=2500
| 25. | Стаж работы (лет) | ||||||
| Число работников |
N=2200
| 26. | Стаж работы (лет) | ||||||
| Число работников |
N=2000
| 27. | Стаж работы (лет) | ||||||
| Число работников |
N=700
| 28. | Стаж работы (лет) | ||||||
| Число работников |
N=1400
| 29. | Стаж работы (лет) | ||||||
| Число работников |
N=1000
| 30. | Стаж работы (лет) | ||||||
| Число работников |
N=800
Типический отбор
N, n – объемы соответственно генеральной и выборочной совокупностей;
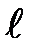 – число типических групп;
– число типических групп;
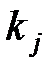 – число вариант в j-ой группе
– число вариант в j-ой группе 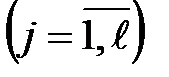 ;
;
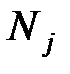 ,
, 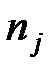 - объемы j-ой типической группы соответственно генеральной и выборочной совокупностей;
- объемы j-ой типической группы соответственно генеральной и выборочной совокупностей;
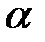 – коэффициент пропорциональности отбора;
– коэффициент пропорциональности отбора;
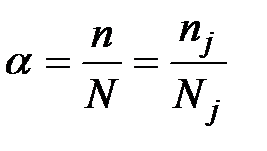 ,
, 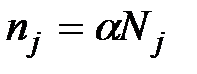 ,
, 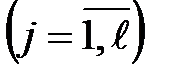 ,
, 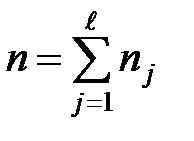 .
.
Теорема Чебышева – Ляпунова
для средней:
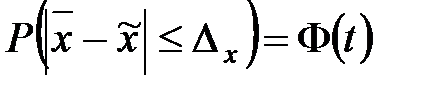 ,
,
для доли:
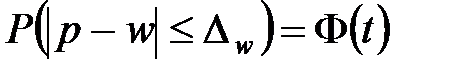 .
.
Выборочные характеристики в типических группах:
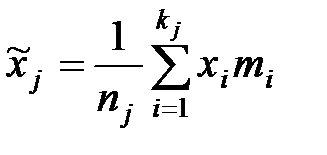 ,
, 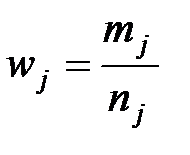 ,
, 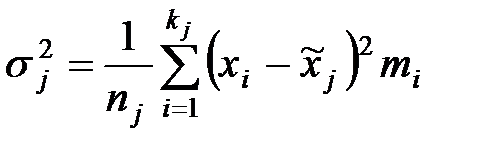 ,
,
где 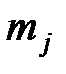 - число единиц, обладающих изучаемым (характерным) признаком в j-ой типической группе.
- число единиц, обладающих изучаемым (характерным) признаком в j-ой типической группе.
Общие выборочные характеристики:
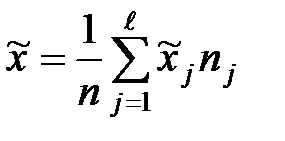 ,
,
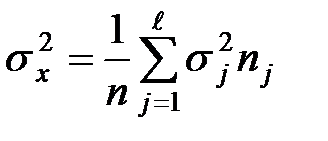 ,
,
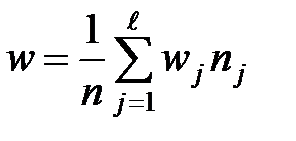 ,
,
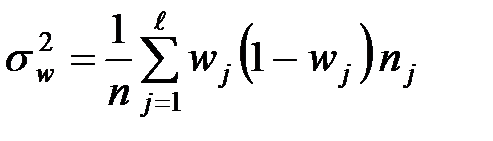 .
.
Предельные ошибки:
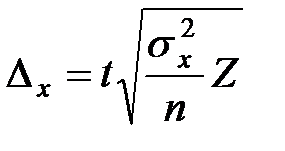 ,
, 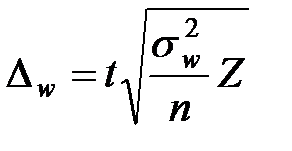 ,
,
где 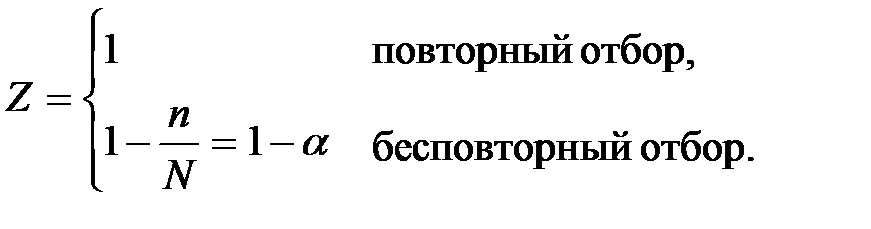
Доверительный интервал
для средней:
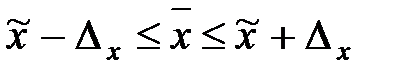 ,
,
для доли:
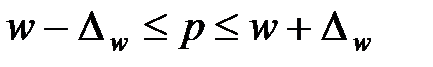 .
.
Задача 1. Для определения средней урожайности пшеницы в области произведена 20% типическая выборка с отбором единиц пропорционально посевной площади участков. Результаты выборки представлены в таблице.
| Участки | Урожайность пшеницы (ц/га) | ||||
| 16,5 – 17,5 | 17,5 – 18,5 | 18,5 – 19,5 | 19,5 – 20,5 | 20,5 – 21,5 | |
| I | Ошибка! Объект не может быть создан из кодов полей редактирования. | 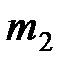 | Ошибка! Объект не может быть создан из кодов полей редактирования. | ||
| II | 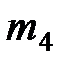 | 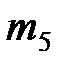 | 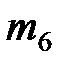 | ||
| III | 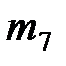 | Ошибка! Объект не может быть создан из кодов полей редактирования. | 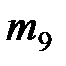 | 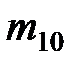 |
I. Определить
а) Средние урожайности 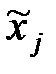 и дисперсии
и дисперсии 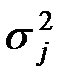 по участкам.
по участкам.
б) Доли участков 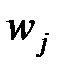 с урожайностью не мене 18,5 ц/га по участкам.
с урожайностью не мене 18,5 ц/га по участкам.
Результаты считать с тремя знаками после запятой. Сам результат округлить до двух знаков после запятой.
Результаты разместить в таблице
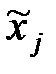 | 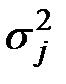 | 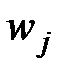 | 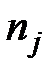 | |
| I | ||||
| II | ||||
| III |
II. Определить
1) с вероятностью 0,9545 доверительный интервал, в котором заключена средняя урожайность пшеницы в области; 2) с вероятностью 0,9973 доверительный интервал для доли посевной площади, имеющей урожайность не менее 18,5 ц/га.
| Номер варианта | 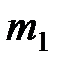 | 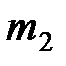 | 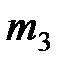 | 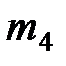 | 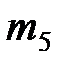 | 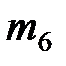 | 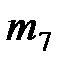 | 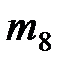 | 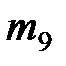 | 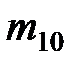 |
| Номер варианта | 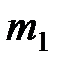 | 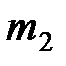 | 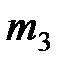 | 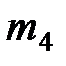 | 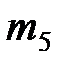 | 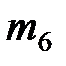 | 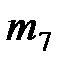 | 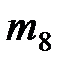 | 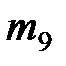 | 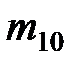 |
Задача 2. В районе N семей, из них 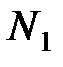 – число семей рабочих,
– число семей рабочих, 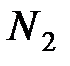 – число семей служащих,
– число семей служащих, 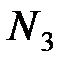 – число семей колхозников. Для определения числа детей в семье была проведена 10%-ная типическая выборка с отбором единиц пропорционально численности единиц типических групп (внутри типических групп применялся метод случайного бесповторного отбора). Результаты выборки представлены в таблице.
– число семей колхозников. Для определения числа детей в семье была проведена 10%-ная типическая выборка с отбором единиц пропорционально численности единиц типических групп (внутри типических групп применялся метод случайного бесповторного отбора). Результаты выборки представлены в таблице.
| Типы семей | Число семей в районе | Среднее число детей в семье | Среднее квадратическое отклонение |
| Рабочие | 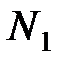 | 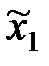 | 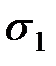 |
| Служащие | 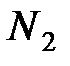 | 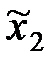 | 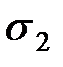 |
| Колхозники | 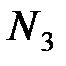 | 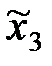 | 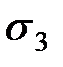 |
| Номер варианта | 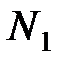 | 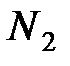 | 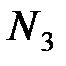 | 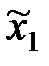 | 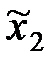 | 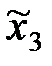 | 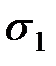 | 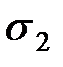 | 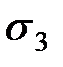 |
| 2,5 2,6 2,1 1,8 1,5 | 1,8 1,5 1,9 2,5 1,4 | 2,2 2,0 1,4 2,2 2,0 | 0,5 0,6 0,7 1,0 0,9 | 1,0 0,5 0,4 0,7 1,0 | 0,7 0,9 0,6 0,5 0,6 | ||||
| Номер варианта | 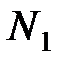 | 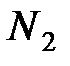 | 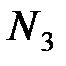 | 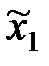 | 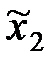 | 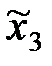 | 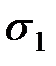 | 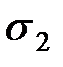 | 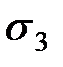 |
| 1,2 2,2 2,0 1,3 2,2 1,4 2,1 2,5 1,5 2,1 1,8 1,7 1,6 1,5 1,4 1,2 2,0 2,1 1,5 2,5 2,0 1,7 2,0 1,2 1,6 | 1,6 1,8 1,9 2,3 2,5 1,6 1,3 2,2 1,4 1,3 2,2 1,6 1,5 2,0 1,3 1,1 1,5 1,4 0,9 2,0 1,0 1,1 2,5 1,5 0,9 | 2,3 2,5 2,0 1,6 1,8 0,9 1,0 1,8 0,8 1,2 2,5 1,4 1,3 2,5 1,5 1,0 2,5 1,4 1,7 1,5 1,4 1,4 1,5 2,1 1,1 | 0,7 0,7 1,0 0,8 0,5 0,6 0,7 1,0 0,9 1,0 0,7 0,6 0,8 1,5 0,9 0,6 0,5 0,9 0,7 1,5 0,5 0,7 1,0 0,6 0,5 | 0,8 0,5 0,6 0,7 0,7 0,5 0,4 0,5 0,8 0,7 1,0 0,4 0,9 0,8 0,7 0,5 1,5 0,7 0,8 1,0 0,6 0,8 0,7 0,8 0,4 | 0,9 1,0 0,8 0,9 1,0 0,3 0,4 0,7 0,5 0,7 0,5 0,5 0,6 1,0 0,6 0,3 1,0 0,4 0,5 0,8 0,7 0,8 0,5 1,0 0,3 |
С вероятностью 0,9545 определить доверительный интервал, в которых находится среднее число детей в семье по данному району.
Задача 3. Для определения доли рабочих завода, не выполняющих норму выработки, была произведена 10%-ная типическая выборка рабочих с отбором числа рабочих пропорционально численности типических групп (внутри типических групп применялся метод случайного бесповторного отбора). Результаты выборки представлены в таблице.
| Цехи | Число рабочих в выборке | Доля рабочих, выполняющих норму выработки (%) |
| I | 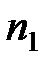 | 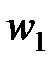 |
| II | 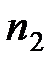 | 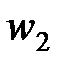 |
| III | 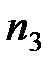 | 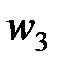 |
| Номер варианта | 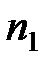 | 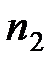 | 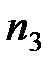 | 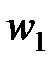 | 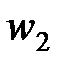 | 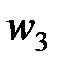 |
С вероятностью 0,9545 определить доверительный интервал, в котором находится доля рабочих завода, не выполняющих норму выработки.
Задача 4. Для определения доли рабочих, имеющих стаж работы более 10 лет, произведена 10%-ная типическая выборка служащих с отбором единиц пропорционально численности типических групп (внутри типических групп применялся метод случайного бесповторного отбора). Результаты выборки представлены в таблице.
| Цехи | Число рабочих в выборке | Доля рабочих, выполняющих норму выработки (%) |
| I | 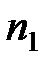 | 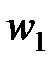 |
| II | 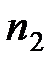 | 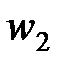 |
| III | 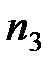 | 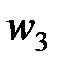 |
| Номер варианта | 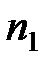 | 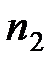 | 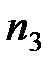 | 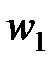 | 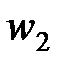 | 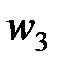 |
Определить вероятность того, что доля служащих, имеющих стаж работы более 10 лет на предприятии, отличается от полученной в выборке по абсолютной величине не более, чем на 0,1 г.
Рекомендуемая литература
1. Математика для экономических специальностей вузов. Ч. 2 / Под ред. Р.Ш. Марданова – Казань: Изд-во КФЭИ, 2001. - Гл.. 18, с. 141 – 172.
2. Сборник задач по математике для экономистов: учебное пособие под ред. проф. Р.Ш. Марданова. – Казань: Изд-во КГУ, 2009. - Гл.. 18, №№18.33 – 18.40.
Индивидуальная работа №6
