Проверка гипотез о виде распределения. критерий согласия пирсона
Одной из важных задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по эмпирическому распределению, представляющему вариационный ряд. Предположение о виде закона распределения можно сделать по гистограмме или полигону (Рис. 4.3)
| а) | б) | в) |
Рис. 4.3. Возможные виды гистограмм:
а) нормального, б) показательного, в) равномерного распределений
Например, по гистограмме (рис. 4.3, а)) можно сделать предположение о том, что генеральная совокупность распределена по нормальному закону.
Для проверки гипотез о виде распределения служат специальные критерии — критерии согласия. Они отвечают на вопрос: согласуются ли результаты экспериментов с предположением о том, что генеральная совокупность имеет заданное распределение.
Проверим это предположение с помощью критерия согласия Пирсона. В этом критерии мерой расхождения между гипотетическим (предполагаемым) и эмпирическим распределением служит статистика
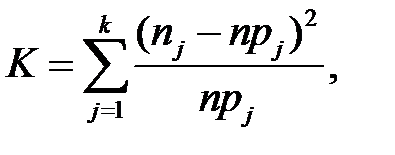
где n — объем выборки;
k — количество интервалов (групп наблюдений);
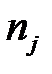 — количество наблюдений, попавших в j-й интервал;
— количество наблюдений, попавших в j-й интервал;
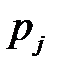 — вероятность попадания в j-й интервал случайной величины, распределенной по гипотетическому закону.
— вероятность попадания в j-й интервал случайной величины, распределенной по гипотетическому закону.
Если предположение о виде закона распределения справедливо, то статистика Пирсона распределена по закону «хи-квадрат» с числом степеней свободы 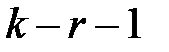 (r — число параметров распределения, оцениваемых по выборке):
(r — число параметров распределения, оцениваемых по выборке): 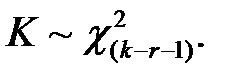
Оцениваются неизвестные параметры с использованием теории точечных оценок (см. источник [3], гл.16 и раздел 3.8. настоящего пособия), некоторые оценки приведены в табл. 4.4.
Таблица 4.4. Оцениваемые параметры и их точечные оценки
| Вид распределения | Оцениваемые параметры | Точечные оценки параметров |
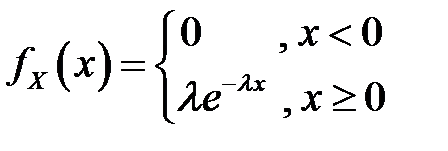 | 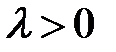 | 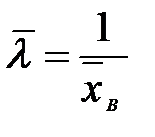 |
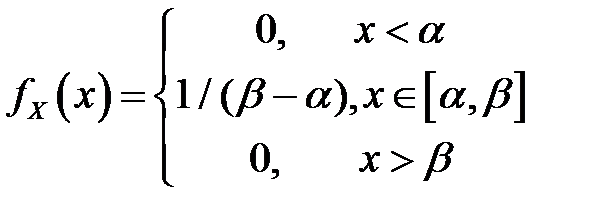 | 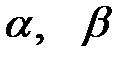 | 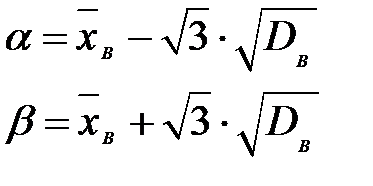 |
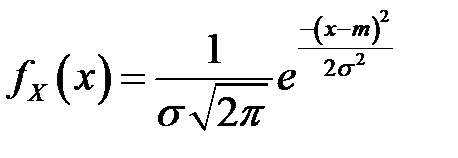 | 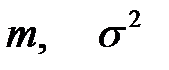 | 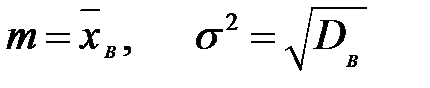 |
Здесь 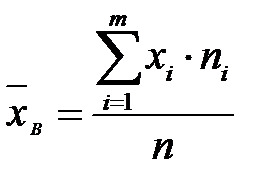
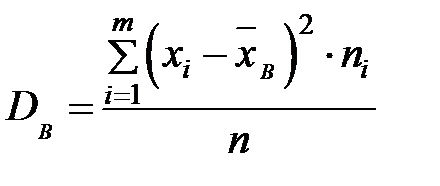 .
.
Количество интервалов k рекомендуется рассчитывать по формуле Старджеса 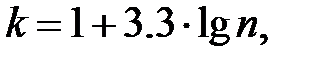 где n — объем выборки. Длину i-го интервала принимают равной
где n — объем выборки. Длину i-го интервала принимают равной 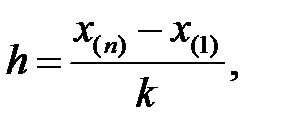 где
где 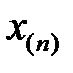 —наибольшее, а
—наибольшее, а 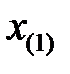 — наименьшее значение в вариационном ряду.
— наименьшее значение в вариационном ряду.
Пример 4.8.Длясреднего балла среди 30-ти групп (с точностью до сотых долей балла) получили выборку 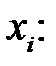
3.7, 3.85, 3.7, 3.78, 3.6, 4.45, 4.2, 3.87, 3.33, 3.76, 3.75, 4.03, 3.8, 4.75, 3.25, 4.1, 3.55, 3.35, 3.38, 3.05, 3.56, 4.05, 3.24, 4.08, 3.58, 3.98, 3.4, 3.8, 3.06, 4.38. Проверить гипотезу о нормальном распределении среднего балла на уровне значимости 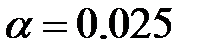 .
.
Решение. Сгруппируем эту выборку. Наименьший средний балл равен 3.05, наибольший — 4.75. Интервал [3; 4.8] разобьем на 6 частей длиной 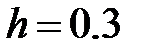 , применяя формулу Старджеса (
, применяя формулу Старджеса ( 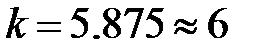 ). Подсчитаем частоту
). Подсчитаем частоту 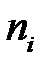 (относительную частоту
(относительную частоту 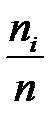 ) для каждого интервала и получим сгруппированный статистический ряд (табл. 4.5).
) для каждого интервала и получим сгруппированный статистический ряд (табл. 4.5).
Таблица 4.5. Статистический ряд
| Интервалы | [3;3.3) | [3.3;3.6) | [3.6;3.9) | [3.9;4.2) | [4.2;4.5) | [4.5;4.8) |
Частоты 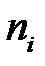 | ||||||
Относительные частоты 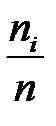 | 0.133 | 0.233 | 0.3 | 0.167 | 0.1 | 0.033 |
Сформулируем основную и альтернативную гипотезы.
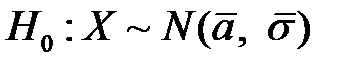 — случайная величина X (средний балл) подчиняется нормальному закону с параметрами
— случайная величина X (средний балл) подчиняется нормальному закону с параметрами 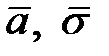 . Так как истинных значений параметров
. Так как истинных значений параметров 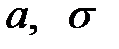 мы не знаем, возьмем их оценки, рассчитанные по выборке:
мы не знаем, возьмем их оценки, рассчитанные по выборке: 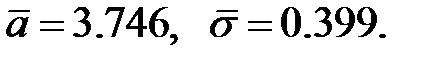
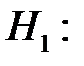 случайная величина X не подчиняется нормальному закону с данными параметрами.
случайная величина X не подчиняется нормальному закону с данными параметрами.
Рассчитаем наблюдаемое значение 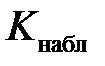 статистики Пирсона. Эмпирические частоты
статистики Пирсона. Эмпирические частоты 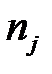 уже известны (табл. 4.5), а для вычисления вероятностей
уже известны (табл. 4.5), а для вычисления вероятностей 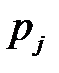 (в предположении, что гипотеза
(в предположении, что гипотеза 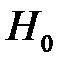 справедлива) применим уже известную формулу (свойство В):
справедлива) применим уже известную формулу (свойство В):
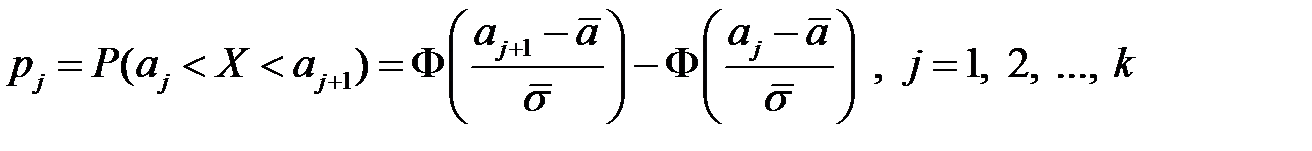
и таблицу функции Лапласа (приложение 1). Полученные результаты сведем в таблицу (табл. 4.6). Наблюдаемое значение статистики Пирсона равно 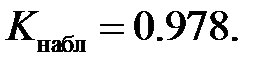
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение 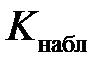 , тем сильнее довод против основной гипотезы. Поэтому критическая область для этой статистики всегда правосторонняя:
, тем сильнее довод против основной гипотезы. Поэтому критическая область для этой статистики всегда правосторонняя: 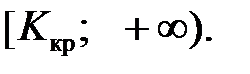 Её границу
Её границу 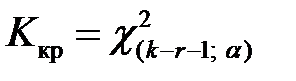 находим по таблицам распределения «хи-квадрат» (приложение 3) и заданным значениям
находим по таблицам распределения «хи-квадрат» (приложение 3) и заданным значениям 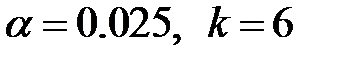 (число интервалов),
(число интервалов), 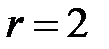 (параметры
(параметры 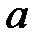 и
и 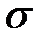 оценены по выборке):
оценены по выборке): 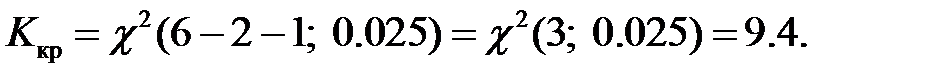
Наблюдаемое значение статистики Пирсона не попадает в критическую область: 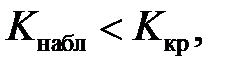 поэтому нет оснований отвергать основную гипотезу.
поэтому нет оснований отвергать основную гипотезу.
Вывод: на уровне значимости 0.025 справедливо предположение о том, что средний балл имеет нормальное распределение.
Таблица 4.6. Сравнение наблюдаемых и ожидаемых частот
| № п/п | Интервалы группировки 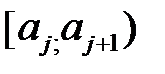 | Наблюдаемая частота 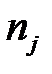 | Вероятность 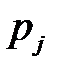 попадания в j-й интервал попадания в j-й интервал | Ожидаемая частота 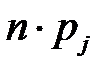 | Слагаемые статистики Пирсона 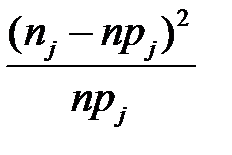 |
| 1. | [3; 3.3) | 0.101 | 3.032 | 0.309 | |
| 2. | [3.3; 3.6) | 0.225 | 6.761 | 0.008 | |
| 3. | [3.6; 3.9) | 0.295 | 8.79 | 0.166 | |
| 4. | [3.9; 4.2) | 0.222 | 6.665 | 0.416 | |
| 5. | [4.2; 4.5) | 0.098 | 2.946 | 0.001 | |
| 6. | [4.5; 4.8) | 0.025 | 0.758 | 0.077 | |
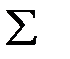 | — | 0.965 | 28.95 | 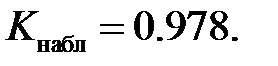 |
3 КОНТРОЛЬНАЯ РАБОТА.
Указания. «Показательные» типовые задачи и примеры находятся по указанным разделам.
| Задача №1 | Тема 2.3 |
| Задача №2 | Тема 2.4 |
| Задача №3 | Темы 2.5–2.7 |
| Задача №4 | Темы 2.8–2.9 |
| Задача №5 | Тема 2.10 |
| Задача №6 | Тема 2.11 |
| Задачи №7–9 | Темы 3.1–3.8 |
Вариант 1
1) Бросаются две игральные кости. Определить вероятность того, что сумма выпавших очков не превосходит трех.
2) В урне три белых и пять черных шаров. Наудачу вынимают два шара. Какова вероятность того, что эти шары разных цветов?
3) Вероятность попадания в цель при одном выстреле равна 0.9. Найти вероятность того, что в результате двух выстрелов будет хотя бы одно попадание.
4) В тире имеется пять винтовок, вероятности попадания в цель из которых равны соответственно 0.5, 0.6, 0,7, 0,8 и 0,9. Найти вероятность попадания в цель из взятой наугад винтовки.
5) 30% изделий некоторого предприятия – продукция высшего сорта. Приобретено 4 изделия этого предприятия. Какова вероятность того, что 2 из них высшего сорта?
6) Найти вероятность того, что среди 300 изделий окажется более трех бракованных, если в среднем бракованные изделия составляют 1,5%.
7) Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка равна 0.5, для второго – 0.4. Х– число попаданий в мишень. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X)и s(Х); в) найти вероятность Р(Х<М(Х)).
8) Дана плотность распределения случайной величины X :
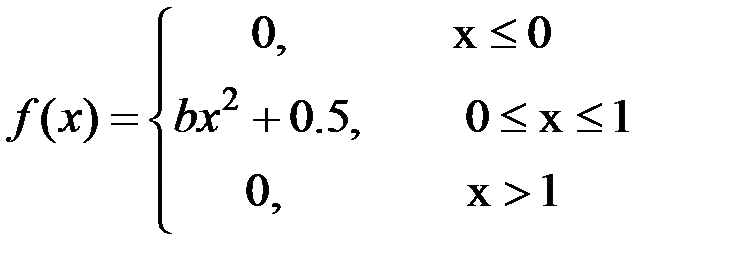
Найти: а) константу b; функцию распределения F(x), в ответ ввести F(l/3); F(l/2); в) МХ; г) DХ; д) Р(1/3 < Х < 1/2).
9) Весы для тяжелых предметов считаются годными, если отклонение X от контрольного веса на более чувствительных весах не превышает 18 г Величина X – нормально распределенная и М(Х)=0, D(X)=10 г. Сколько процентов пригодных весов изготавливает завод? Ответ округлить до целых.
Вариант 2
1) На тридцати карточках написаны числа от 11 до 40. Найти вероятность того, что сумма цифр числа на взятой наугад карточке равна 5–ти или 9–ти.
2) Студент знает 50 из 60 вопросов программы. Найти вероятность того, что студент знает два вопроса, содержащиеся в экзаменационном билете.
3) Игральная кость бросается шесть раз. Найти вероятность того, что число выпавших очков ни разу не повторится.
4) Из урны, содержавшей 3 белых и 7 черных шаров, один шар неизвестного цвета утерян. Найти вероятность извлечь наудачу из урны шар белого цвета.
5) Изделия некоторого предприятия содержат 5% брака. Найти вероятность того, что среди пяти взятых наудачу изделий окажутся два бракованных.
6) Полагая вероятность рождения мальчика равной 0.5, найти вероятность того, что среди 200 новорожденных будет: а) 100 мальчиков, б) от 90 до 110 мальчиков.
7) Из коробки, содержащей 3 синих и 4 красных карандаша, наудачу вынимают 3 карандаша. X – число красных карандашей среди вынутых. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X)и s(Х); в) найти вероятность Р(Х<М(Х)).
8) Задана плотность распределения вероятностей
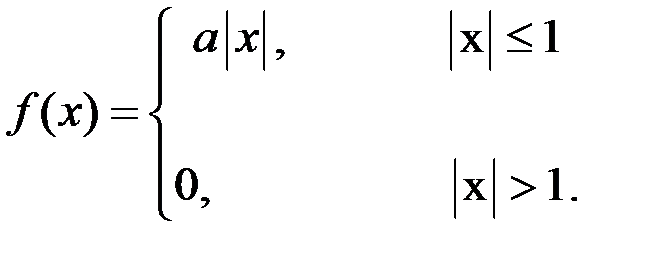
Найти: а) константу а; б) функцию распределения F(x), в ответ ввести значения F(–1/2), F(1/2); в) М(Х); г) D(X); д) Р(–1/2 < X < 2).
9) Компоненты изготовляемого лекарства отвешиваются на весах, ошибка X которых распределена нормально, причём М(Х)= 0, s(Х)= 0.00003 г. Норма веса лекарства 0.02 г. Определить вероятность отбракования лекарства, если максимально допустимый вес принятого к использованию лекарства 0.021г.
Вариант 3
1) В урне 2 красных, 7 зеленых , 5 синих и 10 неокрашенных шаров. Наудачу извлекается один шар. Какова вероятность того, что шар окажется окрашенным?
2) В партии из десяти изделий два бракованных. Наудачу выбирают пять изделий. Какова вероятность того, что среди них одно бракованное?
3) В ящике 10 красных и 6 синих пуговиц. Вынимаются наудачу две пуговицы. Найти вероятность того, что обе пуговицы одного цвета.
4) Имеется десять одинаковых урн, из которых в девяти
находятся по 2 белых и 2 черных шара, а в одной – 5 белых и 1 черный шар. Из взятой наугад урны извлечен белый шар. Какова вероятность того, что шар извлечен из урны, содержавшей 5 белых шаров?
5) Вероятность того, что покупателю потребуется обувь 41–го размера, равна 0,2. Найти вероятность того, что из пяти покупателей только одному потребуется обувь этого размера.
6) Среди семян ржи имеется 0.4% семян сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?
7) Игральная кость бросается до появления шестерки, но не более семи раз. Х– число бросаний кости. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X)и s(Х); в) найти вероятность Р(Х<М(Х)).
8) Задана плотность распределения вероятностей
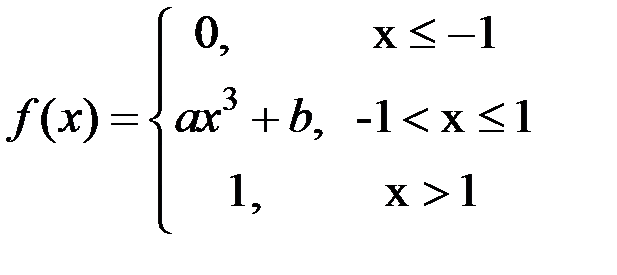
Найти: а) константы а; b б) функцию распределения F(x), в ответ ввести значения F(–1/2), F(1/2); в) М(Х); г) D(X); д) Р(–1/2 < X < 0.5).
9) Издел
10) ие считается пригодным, если отклонение его размера от номинала не превышает по модулю 1.45 мм. Случайные отклонения X распределены нормально, причём М(Х)=0, s(Х)=1.5 мм. Определить вероятность того, что случайно взятое изделие является пригодным.
Список литературы для разделов 1-4.

Список литературы для разделов 5-6.
1. Н.С. Пискунов. Дифференциальное и интегральное исчисление. Т 2, М.: Наука, 1985.
2. Сборник задач по математике для вузов под ред. А.В. Ефимова, Б.П. Демидовича, часть 2,М.: Наука, 1981.
3. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Т 2, 3,М.: Наука, 1970.
4. Г.Н Берман. Сборник задач по курсу математического анализа. М.:Наука, 1976.
5. А.Ф.Филиппов. Сборник задач по дифференциальным уравнениям. М.:Наука, 1973.
Список литературы для раздела 7.

Список литературы для раздела 8.
1. Колобов А.М. Избранные главы высшей математики. – Ч.1. Ряд Фурье. Интеграл Фурье. Операционные исчисления. – М.: Высшая школа, 1985-220с.
2. Ефимов А.В. Математический анализ (специальные разделы) – Ч. 1. Общие функциональные ряды и их приложение. – М.: Высшая школа, 1980. – 279 с.
3. Будак Б.М., Фомин С.В. Кратные интегралы и ряды. – М.: Наука, 1965. – 607 с.
Список литературы для раздела 9.
1. Вентцель Е.С. Теория вероятностей. – М.: Высшая школа. 2004.–576с.
2. Вентцель Е.С. Задачи и упражнения по теории вероятностей. – М.: Высш. шк. 2004. – 166 с.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Высшая школа, 2005.
4. Гмурман В.Е. Теория вероятностей и математическая статистика. Высшая школа, 2004, 480с
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа. 1999. – 415 с.
6. Каган М.Л., Кузина Т.С., Петелина В.Д. Теория вероятностей и математическая статистика в вопросах и задачах : Учеб. пособие / Моск. гос. строит. ун – т. М., 2002. 58с.
7. Каган М.Л. Краткий курс теории вероятностей и математической статистики. Моск. гос. строит. ун.- т. М., 1998. 85с.
8. Магазинников Л.И. Теория вероятностей. – Томск.: ТУСУР, 2000.–150 с
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО САМОСТОЯТЕЛЬНОЙ РАБОТЕ
Направление подготовки 180403 «Судовождение».
Новороссийск
2013 г.
СТРУКТУРА
МЕТОДИЧЕСКИХ РЕКОМЕНДАЦИЯ ПО САМОСТОЯТЕЛЬНОЙ РАБОТЕ СТУДЕНТОВ
СОДЕРЖАНИЕ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:
Интернет-экзамен в сфере профессионального образования
Специальность: 080403 – Судовождение.
Дисциплина: Математика
Время выполнения теста: 45 минут
Количество заданий: 16
Тематическая структура
| N ДЕ | Наименование дидактической единицы ГОС | N | Тема задания |
| Математический анализ | Функции: основные понятия и определения | ||
| Предел функции | |||
| Непрерывность функции. Точки разрыва | |||
| Геометрический и физический смысл производной | |||
| Производные высших порядков | |||
| Приложения дифференциального исчисления ФОП | |||
| Основные методы интегрирования | |||
| Приложения определенного интеграла | |||
| Теория вероятностей | Теоремы сложения и умножения вероятностей | ||
| Полная вероятность. Формула Байеса | |||
| Дискретная случайная величина | |||
| Непрерывная случайная величина | |||
| Математическая статистика | Статистическое распределение выборки | ||
| Характеристики вариационного ряда | |||
| Интервальные оценки параметров распределения | |||
| Проверка статистических гипотез |
Варианты вопросов
Задание 1.( выберите один вариант ответа).
Приращение 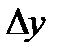 функции
функции 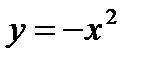 при изменении значения аргумента от – 2 до 3 равно…
при изменении значения аргумента от – 2 до 3 равно…
Варианты ответов:
1) 13; 2) 5; 3) 1; 4) -5.
Задание 2.( выберите один вариант ответа).
Установите соответствие между пределами и их значениями
1. 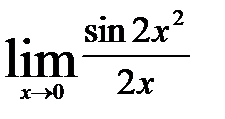 ;
;
2. 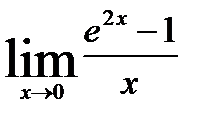 ;
;
3. 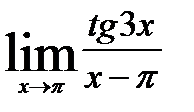 ;
;
Варианты ответов:
1) ∞; 2) 2; 3) 3; 4) 0.
Задание 3.( выберите один вариант ответа).
Установите соответствие между функцией и ее точкой разрыва.
1. 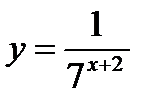 ;
;
2. 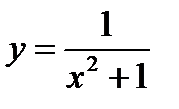 ;
;
3. 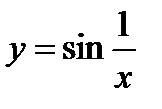 ;
;
4. 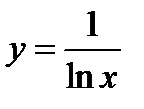
Варианты ответов:
1) Ø; 2) -2; 3) 1; 4) 0.
Задание 4.( выберите один вариант ответа).
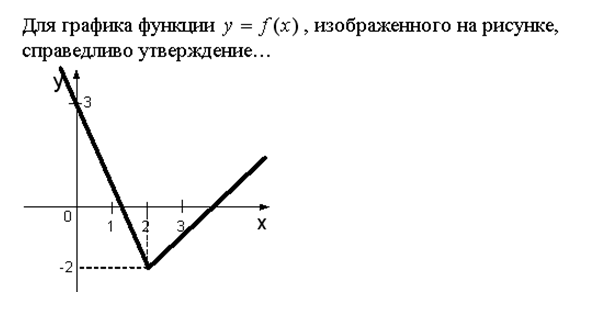
Варианты ответов:
1) f'(2)=-2; 2) f'(2)=2; 3) f'(2) не существует; 4) f'(2)=0.
Задание 5.( выберите один вариант ответа).
Производная второго порядка функции 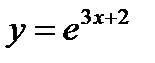 имеет вид…..
имеет вид…..
Варианты ответов:
1) 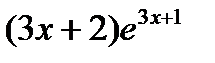 ; 2)
; 2) 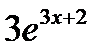 ; 3)
; 3) 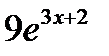 ; 4)
; 4) 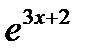
Задание 6.( выберите один вариант ответа).
Функция 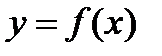 задана на отрезке
задана на отрезке 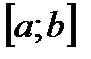 . Укажите количество точек экстремума функции, если график ее производной имеет вид....
. Укажите количество точек экстремума функции, если график ее производной имеет вид....
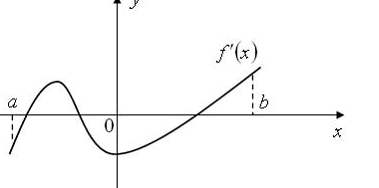
Варианты ответов:
1) 2; 2) 4; 3) 1; 4) 3.
Задание 7.( выберите один вариант ответа).
Установите соответствие между интегралом и его значением.
-
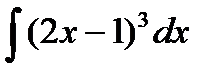 2.
2. 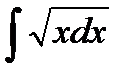 ; 3.
; 3. 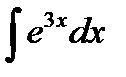 ; 4.
; 4. 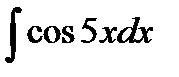
Варианты ответов:
-
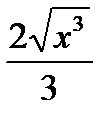 2.
2. 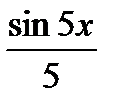 ; 3.
; 3. 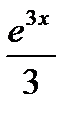 ; 4.
; 4. 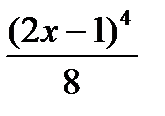
Задание 8.( выберите один вариант ответа).
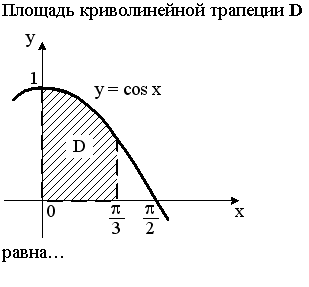
Варианты ответов:
-
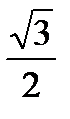 2.
2. 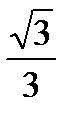 ; 3.
; 3. 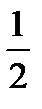 ; 4.
; 4. 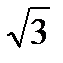 .
.
Задание 9.( выберите один вариант ответа).
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
Варианты ответов:
1) 0,9; 2) 0,2; 3) 1; 4) 0,1.
Задание 10.( выберите один вариант ответа).
Имеются две одинаковые на вид урны. В первой урне один белый и два черных шара, во второй – два белых и пять черных. Из наудачу взятой урны достают один шар. Вероятность того, что этот шар белый, равна…
Варианты ответов:
1) 3/7; 2) 13/21; 3) 1; 4) 13/42.
Задание 11. ( выберите один вариант ответа).
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
| X | -1 | |
| P | 0.6 | 0.4 |
Тогда математическое ожидание этой случайной величины равно…
Варианты ответов:
1) 1,4; 2) 1; 3) 2,6; 4) 2.
Задание 12. ( выберите один вариант ответа).
Непрерывная случайная величина X задана плотностью распределения вероятностей
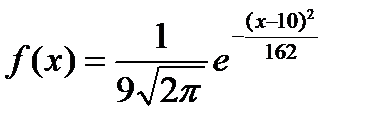
Тогда математическое ожидание этой нормально распределённой случайной величины равно …
Варианты ответов:
1) 9; 2) 162; 3) 10; 4) 81.
Задание 13. ( выберите один вариант ответа).
Из генеральной совокупности извлечена выборка объема n=50, полигон частот которой имеет вид
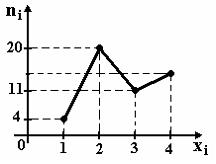 Тогда число вариант xi=4 в выборке равно… Варианты ответов: 1) 15; 2) 14; 3) 50; 4) 4. Задание 14.( выберите один вариант ответа). Мода вариационного ряда 1,1,2,5,7,8 равна… (1) Варианты ответов: 1) 1; 2) 24; 3) 2; 4) 8. Задание 15. ( выберите один вариант ответа). Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид …(8,5 ; 11,5). Варианты ответов: 1) (10,5;11,5) 2) (8;10); 3) (8,5;13,5); 4) (8,5;11,5). Задание 16. ( выберите один вариант ответа). Если основная гипотеза имеет вид Н0: а = 14 то конкурирующей может быть гипотеза … Н1: а ≠ 14 Варианты ответов: 1) Н1: а ≠ 14 2) Н1: а≥ 14; 3) Н1: а ≤ 14); 4) Н1: а ≠ 24. Тогда число вариант xi=4 в выборке равно… Варианты ответов: 1) 15; 2) 14; 3) 50; 4) 4. Задание 14.( выберите один вариант ответа). Мода вариационного ряда 1,1,2,5,7,8 равна… (1) Варианты ответов: 1) 1; 2) 24; 3) 2; 4) 8. Задание 15. ( выберите один вариант ответа). Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид …(8,5 ; 11,5). Варианты ответов: 1) (10,5;11,5) 2) (8;10); 3) (8,5;13,5); 4) (8,5;11,5). Задание 16. ( выберите один вариант ответа). Если основная гипотеза имеет вид Н0: а = 14 то конкурирующей может быть гипотеза … Н1: а ≠ 14 Варианты ответов: 1) Н1: а ≠ 14 2) Н1: а≥ 14; 3) Н1: а ≤ 14); 4) Н1: а ≠ 24. |
Направление подготовки 180403 «Судовождение».
