Аналитическая геометрия на плоскости.
1. Расстояние между точками 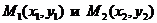 вычисляются по формуле:
вычисляются по формуле:
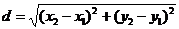 (1)
(1)
2. Координаты точки 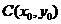 , делящей отрезок
, делящей отрезок  в отношении
в отношении 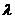 определяется формулами:
определяется формулами:
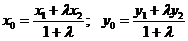 (2)
(2)
При 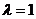 получаем координаты середины отрезка
получаем координаты середины отрезка  :
:
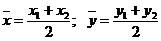
 (3)
(3)
3. Уравнение вида:
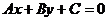 (4)
(4)
где А и В одновременно не обращаются в ноль, называется общим уравнением прямой.
Вектор 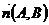 - нормальный вектор прямой (4)
- нормальный вектор прямой (4)
4. Уравнение прямой, проходящей через данную точку 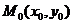 и перпендикулярно нормальному вектору
и перпендикулярно нормальному вектору 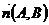 :
:
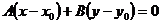 (5)
(5)
5. Уравнение прямой, проходящей через точку 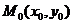 и параллельно вектору
и параллельно вектору  :
:
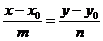 (6)
(6)
6. Уравнение прямой с угловым коэффициентом имеет вид:
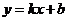 (7)
(7)
где 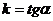 , угловой коэффициент, b – отрезок, отсекаемый ею на оси Oy.
, угловой коэффициент, b – отрезок, отсекаемый ею на оси Oy.
7. Уравнение прямой, проходящей через две точки 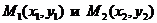 :
:
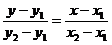 (8)
(8)
8. Уравнение прямой, проходящей через точку 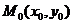 в данном направлении:
в данном направлении:
 (9)
(9)
9. Уравнение прямой в отрезках имеет вид:
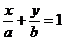 (10)
(10)
Здесь a и b – отрезки, отсекаемые прямой (10) на осях координат.
10. Расстояние точки 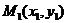 до прямой
до прямой 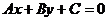 определяется формулой:
определяется формулой:
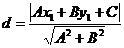 (11)
(11)
11. Угол между прямыми. Условия параллельности и перпендикулярности.
Прямые заданы уравнениями:  | Прямые заданы уравнениями:  и и 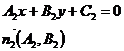 |
1. 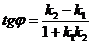 2. Условие параллельности: 2. Условие параллельности: 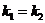 3. Условие перпендикулярности: 3. Условие перпендикулярности: 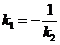 | 1. 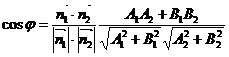 2. Условие параллельности: 2. Условие параллельности: 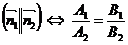 3. Условие перпендикулярности: 3. Условие перпендикулярности: 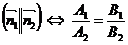 |
Примеры:
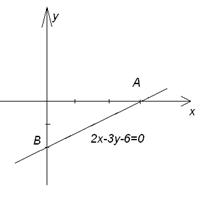
1. Уравнение прямой 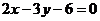 записать в отрезках на осях. Сделать чертеж.
записать в отрезках на осях. Сделать чертеж.
Решение:
Уравнение прямой в отрезках имеет вид:
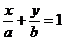 (1)
(1)
Преобразуем уравнение 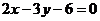 к виду (1):
к виду (1):
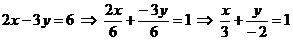
Откладываем на оси Ox три единицы в положительном направлении, а по оси Oy две единицыв направлении противоположном положительному. Получаем точки 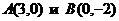 и их соединяем.
и их соединяем.
2. Найти уравнения прямых, проходящих через точку 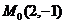 перпендикулярно и параллельно прямой
перпендикулярно и параллельно прямой 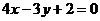 .
.
Решение:
· 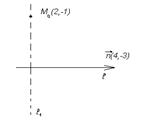 Нормальный вектор
Нормальный вектор 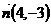 прямой
прямой 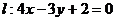 можно выбрать в качестве направляющего вектора искомой прямой
можно выбрать в качестве направляющего вектора искомой прямой 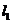 . Воспользуемся для нахождения искомой прямой уравнением
. Воспользуемся для нахождения искомой прямой уравнением 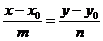 .
.
Тогда 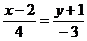 или
или 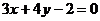 - искомое уравнение.
- искомое уравнение.
·  Так как прямая
Так как прямая 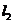 параллельна прямой
параллельна прямой 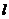 , то в качестве нормального вектора прямой
, то в качестве нормального вектора прямой 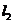 может быть
может быть 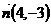 .
.
Используем уравнение: 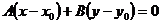 .
.
Здесь 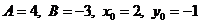 .
.
Искомое уравнение имеет вид:  .
.
3. Найти координаты точки  , симметричной точке
, симметричной точке 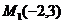 относительно прямой
относительно прямой 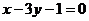 .
.
Решение:
Точки 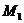 и
и 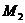 лежат на прямой перпендикулярной данной прямой
лежат на прямой перпендикулярной данной прямой 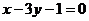 и одинаково удалены от нее.
и одинаково удалены от нее.
Найдем уравнение прямой 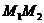 . Угловой коэффициент прямой
. Угловой коэффициент прямой 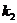 находится из условия
находится из условия 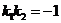 . Так как угловой коэффициент прямой
. Так как угловой коэффициент прямой 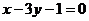 равен
равен 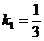 , то
, то 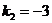 .
.
Запишем уравнение прямой 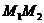 :
:
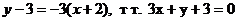
Найдем координаты точки пересечении прямых 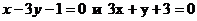 , т.е. решим систему уравнений:
, т.е. решим систему уравнений:
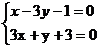 ,
, 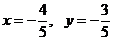 .
.
Точка пересечения прямых 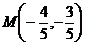 делит отрезок
делит отрезок 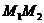 пополам.
пополам.
Воспользуемся формулами деления отрезка пополам:
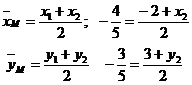
Откуда получаем координаты точки 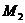 :
: 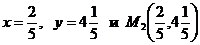 .
.
4. Даны вершины треугольника 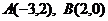 и точка пересечения высот
и точка пересечения высот 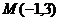 . Найти уравнения сторон треугольника и высоты, опущенной на сторону
. Найти уравнения сторон треугольника и высоты, опущенной на сторону  .
.
Решение:
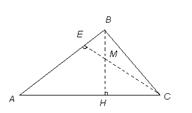 Запишем уравнение прямой
Запишем уравнение прямой  , используя уравнение прямой, проходящей через две заданные точки:
, используя уравнение прямой, проходящей через две заданные точки: 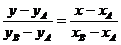 ;
; 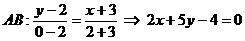 .
.
Уравнение прямой 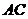 запишем, используя уравнение прямой по точке и нормальному вектору:
запишем, используя уравнение прямой по точке и нормальному вектору:

В качестве нормального вектора 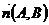 может быть взят вектор
может быть взят вектор 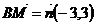 .
.
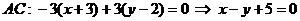
Аналогично найдем уравнение стороны 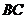 :
: 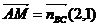 .
.
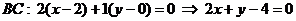
Чтобы найти высоту 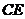 , используем уравнение прямой, проходящей через точку
, используем уравнение прямой, проходящей через точку 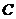 и параллельно вектору
и параллельно вектору  :
: 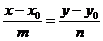 .
.
В качестве направляющего вектора  может быть выбран нормальный вектор прямой
может быть выбран нормальный вектор прямой  :
: 
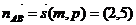
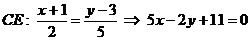
5. Записать с помощью неравенств ту полуплоскость, в которой лежит точка 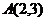 и границей является прямая
и границей является прямая 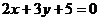 .
.
Решение:
Подставим координаты точки в левую часть уравнения данной прямой:
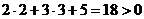
Следовательно, данная точка не лежит на данной прямой, а искомая полуплоскость определяется неравенством: 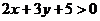 .
.
