Правила построения асимптотических ЛАЧХ.
1) Вычислить 20lgK и сопрягающие частоты 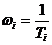 , которые следует пронумеровать в порядке возрастания.
, которые следует пронумеровать в порядке возрастания.
2) На оси абсцисс отметить сопрягающие частоты.
3) Построить первую асимптоту с наклоном - 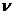 20дБ/дек, проходящую через точку с координатами (1, 20lgK) до первой сопрягающей частоты.
20дБ/дек, проходящую через точку с координатами (1, 20lgK) до первой сопрягающей частоты.
4) Построить вторую асимптоту, которая проводится из конца первой асимптоты до второй сопрягающей частоты. Ее наклон изменяется на 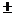 20дБ/дек или на
20дБ/дек или на 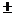 40дБ/дек по отношению к первой асимптоте в зависимости от того, звеном первого или второго порядка является звено, которому соответствует первая сопрягающая частота. Знак плюс берется, если изменение наклона ЛАЧХ обусловлено форсирующими звеньями, знак минус, если изменение наклона обусловлено инерционным или колебательным звеньями.
40дБ/дек по отношению к первой асимптоте в зависимости от того, звеном первого или второго порядка является звено, которому соответствует первая сопрягающая частота. Знак плюс берется, если изменение наклона ЛАЧХ обусловлено форсирующими звеньями, знак минус, если изменение наклона обусловлено инерционным или колебательным звеньями.
5) Построить остальные асимптоты аналогично второй, изменяя наклоны на частотах сопряжения.
Последняя асимптота начинается из конца асимптоты, заканчивающейся на последней сопрягающей частоте, и уходит в бесконечность.
Пример вычисления и построения логарифмических частотных характеристик приведен в приложении.
Задание 3
Условие задачи
Преобразовать структурную схему разомкнутой системы и определить ее передаточную функцию. Замкнув систему единичной отрицательной обратной связью, определить передаточную функцию замкнутой систем относительно выходной переменной. Проверить замкнутую систему на устойчивость по критерию Рауса.
Вид схемы (рисунок 4.1) определить по сумме последней и предпоследней цифр номера зачетной книжки согласно таблице 4.1, а параметры звеньев – по последней цифре (таблица 4.2).
Таблица 4.1- Вид схемы
| Вариант | ||||||||||
| Схема | а | б | в | г | д | е | ж | и | к | л |
Таблица 4.2 - Параметры звеньев
| Параметры звеньев | Вариант | |||||||||
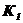 | ||||||||||
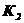 | 2,5 | 5,5 | 0,5 | |||||||
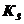 | 0,8 | 4,5 | 0,25 | 6,5 | 0,8 | 1,5 | ||||
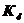 | 3,5 | 2,5 | 5,5 | 6,5 | 0,5 | 1,6 | 0,8 | |||
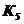 | 2,5 | 3,8 | 4,5 | 8,5 | 6,5 | |||||
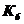 | 4,8 | 0,6 | 1,75 | 6,5 | 8,45 | 2,5 | ||||
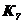 | 0,5 | 0,6 | 0,8 | 0,35 | 0,4 | 0,85 | 0,15 | 0,25 | 0,55 | 0,9 |
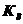 | 1,2 | 1,5 | 0,5 | 0,8 | 0,45 | 0,95 | 1,4 | 2,5 | ||
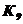 | 3,5 | 2,5 | 0,85 | 5,5 | 4,5 | |||||
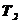 | 1,5 | 0,85 | 1,25 | 0,1 | 0,25 | 0,5 | ||||
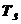 | 0,1 | 0,2 | 0,35 | 0,8 | 0,4 | 0,55 | 0,5 | 0,85 | 1,5 | 0,6 |
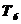 | 0,4 | 0,25 | 1,5 | 0,05 | 1,5 | 0,75 | 1,25 | 0,08 | ||
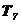 | 0,15 | 0,3 | 0,45 | 0,35 | 0,6 | 0,095 | 0,2 | 0,4 | 0,05 | 0,85 |
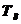 | 0,5 | 0,1 | 0,2 | 0,065 | 0,02 | 0,42 | 0,08 | 0,012 | 0,15 | 0,05 |
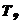 | 0,08 | 0,25 | 0,12 | 0,06 | 0,009 | 1,15 | 0,5 | 0,2 | 0,35 | 0,15 |
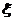 | 0,25 | 0,4 | 0,6 | 0,75 | 0,45 | 0,3 | 0,5 | 0,35 | 0,55 | 0,8 |

a)
 | |||||||
|
| ||||||
| |||||||

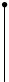








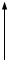 |
|
 | |||
 | |||
Рисунок 4.1 – Варианты структурных схем
|
|
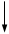


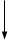

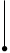 в)
в)  | |||
 |

 г)
г)
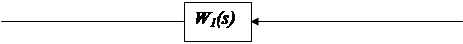 | |||
 |
д)
 |

 е)
е)

 ж)
ж)
Продолжение рисунка 4.1
 | |||
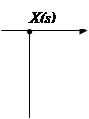 |
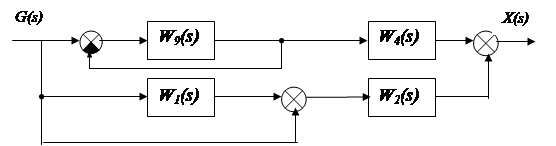
 и)
и)
 |
к)
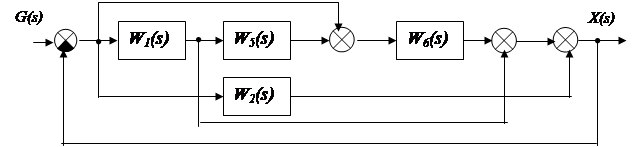 |
л)
Продолжение рисунка 4.1
Передаточные функции звеньев структурной схемы приведены в таблице 4.3.
Таблица 4.3 – Передаточные функции звеньев
| № | Тип звена | Передаточная функция |
| пропорциональное | 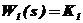 | |
| апериодическое первого порядка | 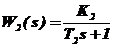 |
Продолжение таблицы 4.3
| пропорциональное | 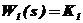 | |
| апериодическое первого порядка | 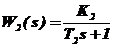 | |
| колебательное | 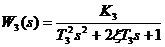 | |
| интегрирующее | 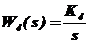 | |
| апериодическое первого порядка | 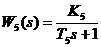 | |
| форсирующее | 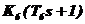 | |
| реальное дифференцирующее | 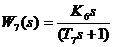 | |
| реальное интегрирующее | 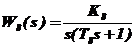 | |
| колебательное | 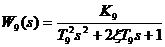 |
4.2 Правила преобразования структурных схем
Структурной схемой в теории автоматического управления называют графическое изображение математической модели системы автоматического управления в виде соединения звеньев. Звенья представляют в виде прямоугольников, внутри которых записывают их передаточные функции.
При изображении структурных схем систем автоматического регулирования и управления используют условные обозначения, приведенные в приложении В.
Входные и выходные переменные записывают в виде изображений по Лапласу, если передаточные функции задают в изображениях Лапласа. Если же передаточные функции задают в операторной форме, то входные и выходные переменные записывают в виде оригиналов.
Основными типами соединений звеньев в структурной схеме являются последовательное, параллельное и встречно-параллельное (с обратной связью). Эти соединения звеньев можно заменить одним звеном с эквивалентной передаточной функцией, пользуясь правилами преобразования структурных схем (первые три правила приложения Г).
Если при размыкании главной обратной связи системы автоматического регулирования получится цепь, содержащая параллельные или обратные связи, то такая система называется многоконтурной. Многоконтурная система может иметь структуру с перекрестными связями. В этом случае контур обратной или параллельной связи охватывает участок цепи, содержащий начало или конец другой цепи параллельной или обратной связи.
Пользуясь структурными преобразованиями, можно любую систему автоматического регулирования привести к расчетному виду, исключающему перекрестные связи и позволяющему получить объединенные (эквивалентные) передаточные функции разомкнутой а) и замкнутой б) систем автоматического регулирования (рисунок 4.2).
| |||
| |||





 G(s) Y(s) G(s) X(s)
G(s) Y(s) G(s) X(s)
 |

а) б)
Рисунок 4.2 - Разомкнутая и замкнутая системы
На рисунке 4.2 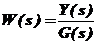 - передаточная функция разомкнутой системы.
- передаточная функция разомкнутой системы.
Передаточная функция замкнутой системы
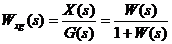 .
.
Критерий устойчивости Рауса
Условие устойчивости линейной системы формулируется следующим образом: для того, чтобы линейная система была асимптотически устойчивой, необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательную вещественную часть (были левыми), т.е. на комплексной плоскости корней располагались левее мнимой оси.
Вычисление корней характеристического уравнения выше второго порядка связаны с большими трудностями. Поэтому важное значение приобретают правила, которые позволяют определять устойчивость системы без определения корней. Эти правила называют критериями устойчивости. Существующие критерии делятся на алгебраические и частотные. Одним из алгебраических критериев является критерий Рауса.
Для проверки устойчивости по критерию Рауса необходимо иметь характеристическое уравнение замкнутой системы автоматического регулирования в виде:
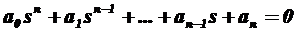 . (6)
. (6)
Характеристическое уравнение может быть получено путем выделения знаменателя передаточной функции (1) и приравнивания его к нулю.
По характеристическому уравнению составляется таблица Рауса.
Таблица 2.6 – Таблица Рауса
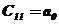 | 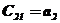 | 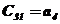 | 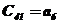 | … | |
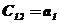 | 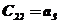 | 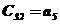 | 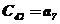 | … | |
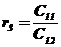 | 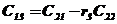 | 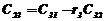 | 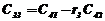 | 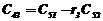 | … |
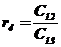 | 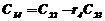 | 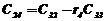 | 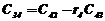 | 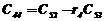 | … |
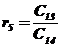 | 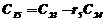 | 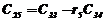 | 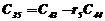 | 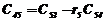 | … |
В первых двух строках таблицы записывают коэффициенты характеристического уравнения. Любой из коэффициентов 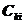 при i
при i 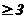 (k – номер столбца, i – номер строки) находится по формуле
(k – номер столбца, i – номер строки) находится по формуле
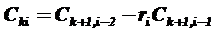 , ( 7)
, ( 7)
где 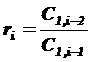 .
.
Число строк таблицы Рауса на единицу больше степени характеристического уравнения. Если при вычислении индекса получается отрицательное число, то соответствующий коэффициент равен нулю.
Критерий устойчивости Рауса формулируется следующим образом. Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были положительными, т.е. чтобы 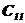 >0;
>0; 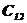 >0; …;
>0; …; 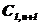 >0. Если при расчете в предпоследней строке первого столбца таблицы получится нуль, это значит, что система находится на границе устойчивости.
>0. Если при расчете в предпоследней строке первого столбца таблицы получится нуль, это значит, что система находится на границе устойчивости.
Методические указания
Для выполнения задания необходимо проработать теоретический материал по учебнику [1, с. 64-77, с.114-137] или по [2, с. 195-216, с.250-268].
Преобразование проводят, постепенно избавляясь от перекрестных связей, приводя схему сначала к виду с простыми соединениями (последовательным, параллельным и встречно-параллельным), а затем к простейшей одноконтурной системе, называемой расчетной.
При преобразовании структурной схемы необходимо применять более простые правила преобразования, чтобы избежать появления неэквивалентных линий связи.
Решение задачи рекомендуется выполнять в последовательности:
1) ознакомиться с условием задачи;
2) выяснить, какие типовые звенья входят в структурную схему и какие имеются виды связи между ними;
3) освободиться от перекрестных связей путем применения правил переноса узлов и сумматоров через звенья (приложение Г);
4) преобразовать структурную схему к одноконтурной, пользуясь правилами преобразования (приложение Г);
5) получить объединенную (эквивалентную) передаточную функцию разомкнутой системы;
6) замкнуть систему главной обратной связью и получить передаточную функцию замкнутой системы;
7) подставить в передаточную функцию замкнутой системы выражения для передаточных функций звеньев и преобразовать ее к виду простой дроби;
8) подставить в выражение для передаточной функции численные значения параметров и получить значения коэффициентов.
9) выделить характеристическое уравнение замкнутой системы;
10) записать коэффициенты характеристического уравнения в таблицу Рауса и заполнить все ее столбцы;
11) сделать вывод об устойчивости системы .
Пример решения задачи приведен в Приложении Д.
Задание 4
Условие задачи
По заданному характеристическому уравнению замкнутой системы автоматического регулирования построить кривую D-разбиения плоскости по варьируемому параметру системы и определить границы изменения этого параметра, при которых система остается устойчивой.
Вариант задания определяют по последней цифре суммы последней и предпоследней цифр шифра согласно таблицы 5.1.
Таблица 5.1
| Вариант | Характеристическое уравнение | Варьируемый параметр |
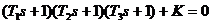 | 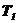 | |
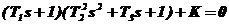 | 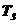 | |
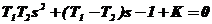 | 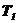 | |
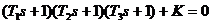 | 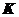 | |
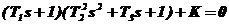 | 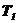 | |
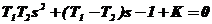 | 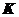 | |
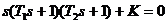 | 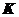 | |
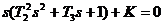 | 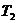 | |
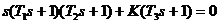 | 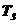 | |
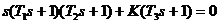 | 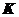 |
Значения неизменяемых параметров уравнения выбрать по предпоследней цифре шифра из таблицы 2.8.
Таблица 5.2
| Параметр | Вариант | |||||||||
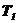 | 2,8 | 0,5 | 0,1 | 0,05 | 0,4 | 1,5 | ||||
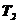 | 0,1 | 0,01 | 0,04 | 0,08 | 0,5 | 0,5 | 1,5 | 0,25 | 0,8 | |
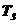 | 0,05 | 0,4 | 0,02 | 0,25 | 0,85 | 0,02 | 0,45 | 0,25 | 1,0 | 0,01 |
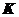 |
Например, номер зачетной книжки 99-24-45, характеристическое уравнение (вариант 9) 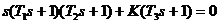 ; варьируемый параметр
; варьируемый параметр 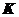 ; неизменяемые параметры (вариант 4):
; неизменяемые параметры (вариант 4): 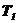 =2;
=2; 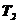 =0,5;
=0,5; 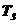 =0,85;
=0,85; 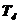 =1,5.
=1,5.
