Задача 5 – Расчет статически неопределимых балок

Задание. Для одной из балок, изображенной на рисунке 19, требуется:

1) построить эпюры поперечных сил 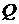и изгибающих моментов ;

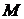2) выполнить статическую и кинематическую проверки;

3) подобрать двутавровое сечение при ;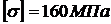

4) определить прогибы в середине межопорного пролета и на

конце консоли.

Данные взять из таблицы 5.

Для раскрытия статической неопределимости балки необходимо воспользоваться методом сил.

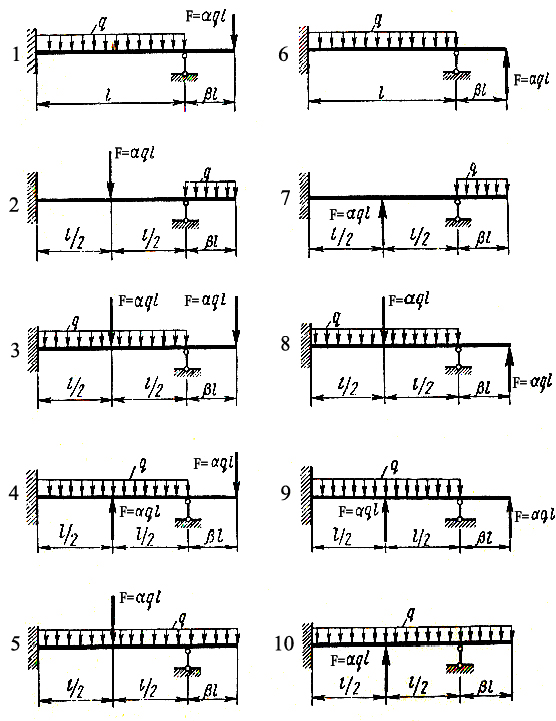
Рисунок 19 – Расчетные схемы статически неопределимых балок

Пример 4. Проведем решение задания для балки, изображенной на рисунке 20.

Решение

1) Находим степень статической неопределимости (число опор-

ных связей минус число уравнений равновесия) 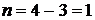. Данная балка один раз статически неопределима.

Таблица 5 – Исходные данные к задаче 5

Схема по рисунку 19	α	β	l	q
м	кН/м
	0,1	0,1
	0,2	0,2
	0,3	0,3
	0,4	0,4
	0,5	0,5
	0,6	0,6
	0,7	0,7
	0,8	0,8
	0,9	0,9
	1,0	1,0
е	г	д	г	д

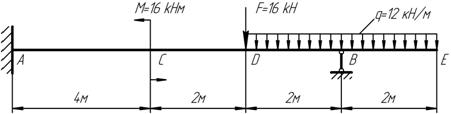
Рисунок 20 – Заданная система балки

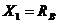2) Выбираем основную систему. Для этого отбросим шарнирную опору и приложим в этом сечении неизвестную силу (рисунок 21).

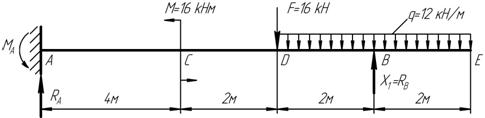
Рисунок 21 – Основная система балки

3) Составляем каноническое уравнение по методу сил:

.

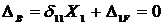4) Для определения перемещения 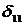от действия единичной на-

грузки 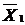и перемещения от действия заданной нагрузки предварительно построим эпюры изгибающих моментов в основной системе при единичном и грузовом состоянии.

Рассмотрим единичное состояние. Для этого построим единичную эпюру (рисунок 22).

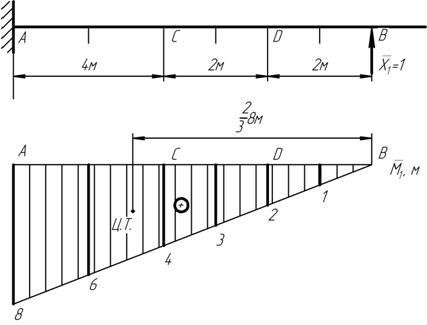
Рисунок 22 – Единичное состояние балки

Для дальнейших расчетов нам необходимы будут значения моментов на концах и в серединах участков балки ( 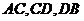). На единичной эпюре укажем значение этих моментов, вычисленных как произведение единичной силы 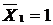на расстояние от нее до рассматриваемой точки ( ).

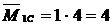Рассмотрим грузовое состояние основной системы (рисунок 23).

Вычислим значение моментов 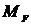в сечениях:

т. : ;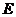

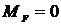т. ;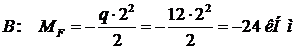

т. ;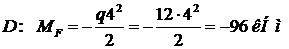

т. ;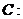

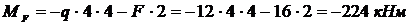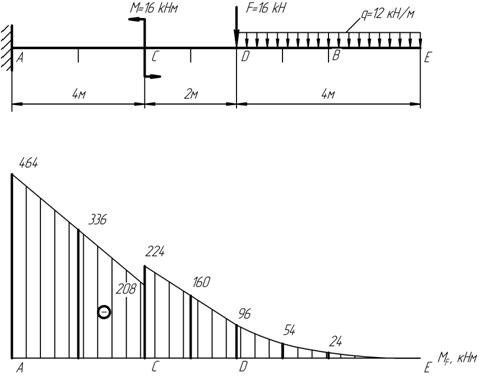
Рисунок 23 – Грузовое состояние балки

т. : ;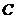

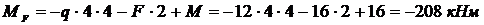т. : .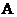

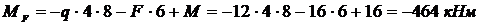По найденным значениям строим эпюру 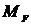(рисунок 23).

Для определения перемещения 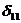воспользуемся формулой Мора:

.

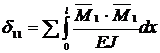Вычисление интеграла осуществляем по правилу Верещагина, «умножая» эпюру 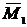саму на себя:

,

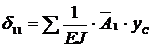где 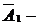площадь единичной эпюры на участке;

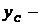ордината единичной эпюры на уровне ее центра тяжести,

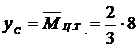
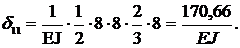
Перемещение 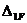определяем «перемножением» эпюр 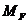и , и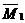спользуя формулу Симпсона:

,

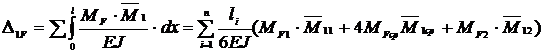где 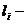длина участка балки;

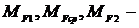значения моментов грузовой эпюры в нача-

ле, средине и конце участка;

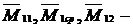значение моментов единичной эпюры в нача-

ле, средине и конце участка.

Напомним, что результат «перемножения» однозначных эпюр является положительным, а разнозначных – отрицательным.

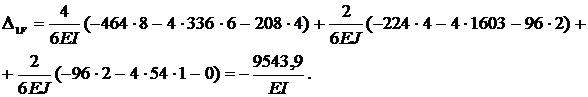
Из уравнения 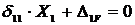находим :

.

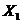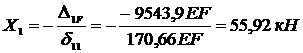Строим скорректированную (исправленную) эпюру 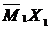(рисунок 24).

Для этого значения эпюры 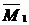(рисунок 22) умножаем на .

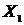Строим окончательную эпюру моментов 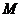(рисунок 24). Для этого складываем эпюры 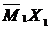(рисунок 24) и 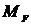(рисунок 23).

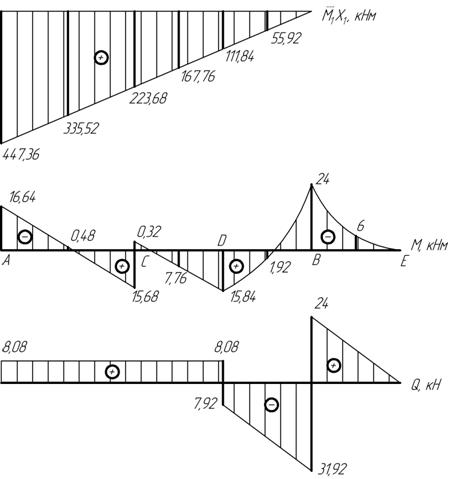
Рисунок 24 – Эпюры изгибающих моментов и поперечных сил

Проведем кинематическую проверку правильности решения. Для этого «перемножим» эпюру 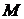(рисунок 24) с единичной эпюрой 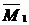(рисунок 22), т.е. определим прогиб основной системы в сечении .

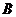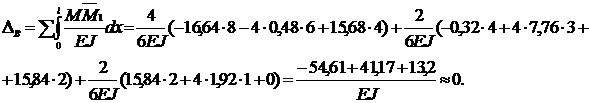
Прогиб в сечении 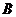основной системы равен нулю, что соответствует условию ее деформации. Следовательно, задача решена правильно.

Для построения эпюры поперечных сил 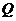используем основную систему и найденное значение .

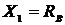Вычисляем поперечные силы .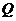

Участок : ;

, , .

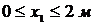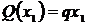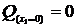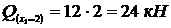Участок : ;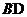

, , .

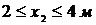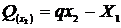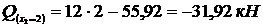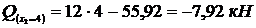Участок : ;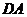

, .

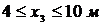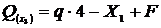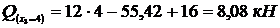По найденным значениям строим эпюру 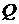(рисунок 24). Следует отметить, что по эпюрам 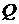и 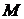можно определить значения реакций в защемлении балки ( , ).

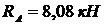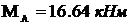Подбираем сечение балки из условия прочности по нормальным напряжениям (опасное поперечное сечение находится над опорой ):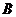

;

.

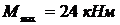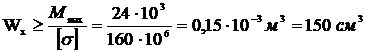Принимаем двутавр № 18 .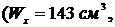

.

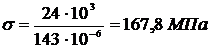Перегруз балки составляет № 18

,

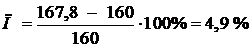что находится в пределах допустимого (5 %).

Для определения прогиба заданной балки в сечении 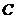используем принятую ранее основную систему и произведем ее расчет на действие единичной силы 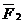, приложенной по направлению искомого прогиба. Соответствующая единичная эпюра изгибающего момента 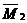приведена на рисунке 25.

«Перемножая» эпюры 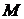и 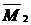, получим

.

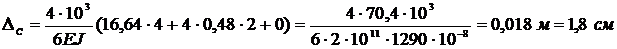Прогиб балки в точке 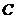направлен вниз, т. е. совпадает с направлением единичной силы.

Для определения прогиба балки в точке 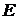приложим в этой точке единичную силу 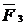, направленную вниз. Эпюра изгибающего момента 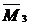изображена на рисунке 25.

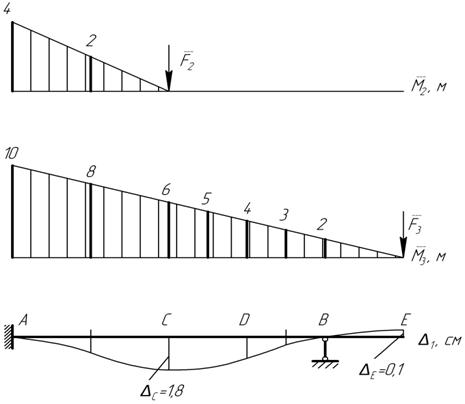
Рисунок 25 – К определению прогибов балки

«Перемножая» эпюры 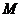и 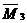, получим

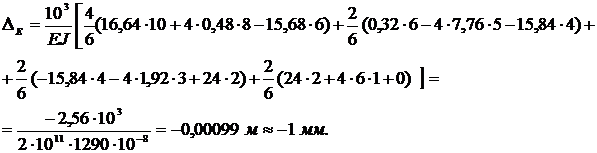
Знак минус означает, что прогиб балки в сечении 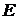направлен не вниз по направлению единичной силы 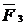, а вверх.

Упругая линия балки изображена на рисунке 25. Причем точки ее перегиба, в которых кривизна оси меняет знак, совпадают с точками пересечения линии эпюры 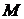с нулевой линией (в точках изменения знака эпюры).

Задача 6 – Внецентренное сжатие

Задание. Чугунный короткий стержень, заданное поперечное сечение которого выбирается из рисунка 26, сжимается продольной силой F, приложенной в точке А. Требуется:

1) вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив эти напряжения через F и размеры сечения;

2) найти допускаемую нагрузку F при заданных размерах сечения и допускаемых напряжениях для чугуна на сжатие [σ]_с и на растяжение [σ]_р.

Данные взять из таблицы 6.

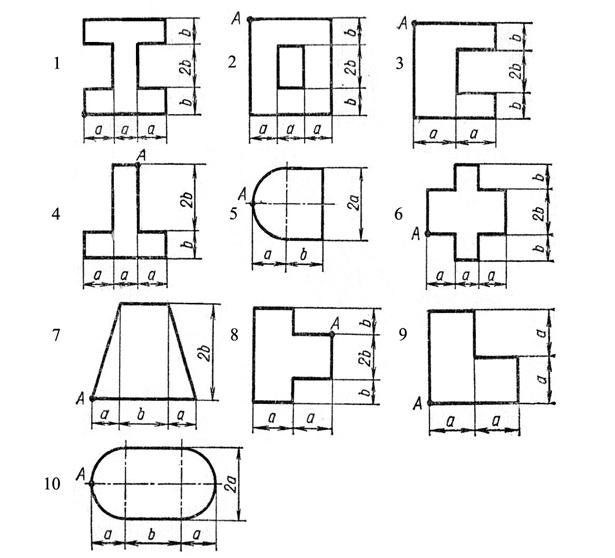
Рисунок 26 – Поперечные сечения стержней

Таблица 4 – Исходные данные к задаче 6

Схема по рисунку 26	а	б	[σ]с	[σ]р	№ строки	Схема по рисунку 26	а	б	[σ]с	[σ]р
см	МПа	см	МПа
е	г	д	г	д		е	г	д	г	д

Пример 6. Проведем решение задания для чугунного короткого стержня, поперечное сечение которого изображено на рисунке 27.

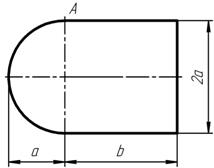
Рисунок 27 – Поперечное сечение стержня

Данные для расчета

а = 0,1 м; в = 0,2 м; 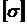_р = 30 МПа; 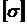_с = 120 МПа.

Решение

1. Вычислим наибольшие растягивающие и сжимающие напряжения в поперечном сечении.

Наибольшие нормальные напряжения возникают в точках, наиболее удаленных от нейтральной линии. Для их определения нужно найти положение этой линии в отрезках, отсекаемых ею на осях Y и Z (рисунок 28):

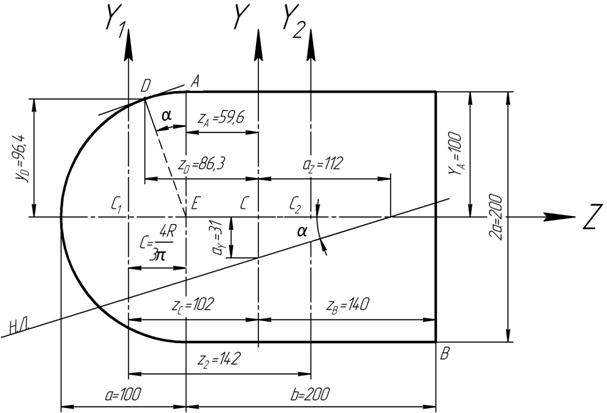
Рисунок 28 – Расчетная схема поперечного сечения стержня

а_z= 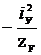; а_y = ,

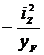где z_F, y_F – координаты точки приложения силы относительно

центральных осей;

i_z = 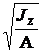и i_y = 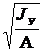– главные радиусы инерции сечения.

Для определения положения центральных осей вычислим координаты центра тяжести сечения

,

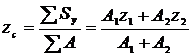где A₁ – площадь полукруга;

A₂ – площадь прямоугольника;

z₁ и z₂ – координаты центров тяжестей в системе координат Z Y₁.

A₁ =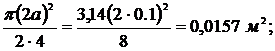

A₂ =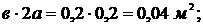

z₁ = 0; z₂ = c +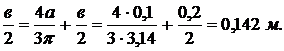

Следовательно,

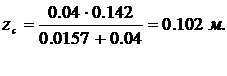
Координата у_с = 0, так как сечение симметрично относительно оси Z. Тогда координаты точки А в центральной системе координат Z Y определяют так:

у_А = у_F = а = 0,1 м; z_A = z_F = –z _c+ c = – 0.102+ .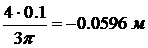

Найденные центральные оси являются для данного сечения главными центральными, так как одна из них совпадает с осью симметрии. Определим главные моменты инерции, воспользовавшись формулами параллельного переноса:

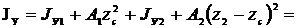
=0,11a⁴+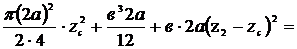

=

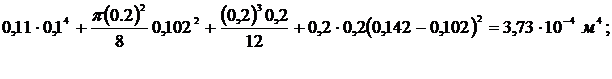
J_z = J_z1 + J _z2 =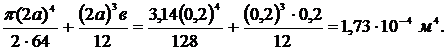

Тогда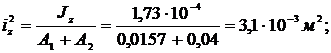

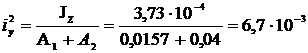м².

Теперь найдем положение нейтральной линии в отрезках, отсекаемых ею на осях координат Y Z:

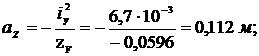
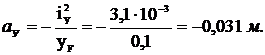
Наиболее удаленные от нейтральной линии точки определим, проведя касательные к контуру сечения, параллельные этой линии. Точки касания В и D являются искомыми точками. Найдем их координаты:

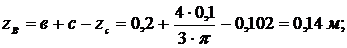у_в = – а = – 0,1 м;

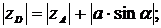
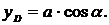
Угол определим из отношения

tg .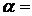

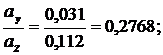
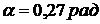Тогда у_D = 0,1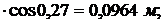

.

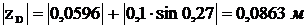С учетом направления оси Z получим z_D = – 0,0863 м.

Вычислим наибольшие сжимающие напряжения в точке D и растягивающие – в точке В.

.

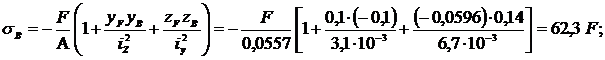
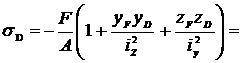
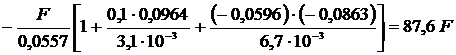2. Определим допускаемую нагрузку из условия прочности растянутых волокон

.

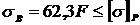Отсюда

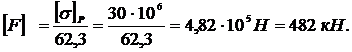
Рассчитаем допускаемую нагрузку из условия прочности сжатых волокон

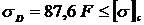
Отсюда

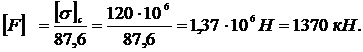
Меньшее из двух полученных значений нагрузки примем за допускаемое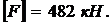

Задача 7 – Построение эпюр внутренних силовых факторов для бруса с ломаной осью

Задание. Для заданного варианта оси ломаного стержня круглого поперечного сечения, расположенной в горизонтальной плоскости, с прямыми углами в точках А и В (рисунок 29),требуется:

1) построить отдельно (в аксонометрии) эпюры изгибающих (М) и крутящих моментов (Т);

2) установить опасное сечение и найти для него расчетный момент по четвертой теории прочности.

На стержень действует вертикальная нагрузка.

Данные взять из таблицы 7.

Пример 7. Проведем решение для ломаного стержня, представленного на рисунке 30а.

Данные для расчета: .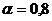

Решение

1. Для построения эпюр внутренних силовых факторов используем метод сечения, определяя величины крутящих и изгибающих моментов как алгебраическую сумму моментов внешних сил, действующих по одну сторону от рассматриваемого сечения. Ординаты эпюры изгибающих моментов будем откладывать на растянутом волокне бруса. Крутящий момент будем считать положительным, если при взгляде в торец отсеченной части этот момент представляется направленным по ходу часовой стрелки.

Участок КВ: 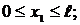Т₁ = 0; М_I = q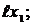

при 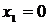М_К = 0; при 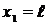М_В = q 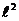(растянуты верхние волокна).

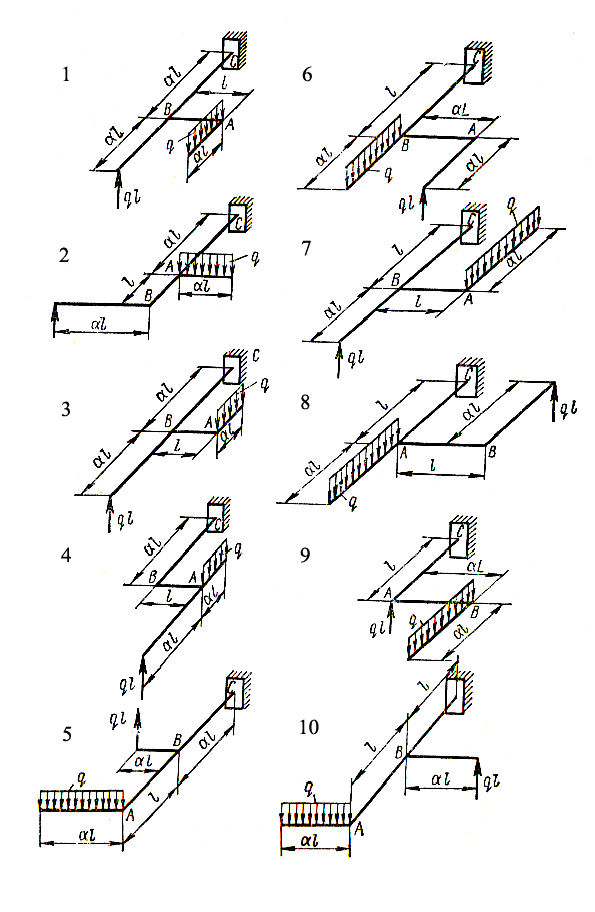
Рисунок 29 - Схемы ломаных стержней

Таблица 5 – Исходные данные к задаче 7

Схема по рисунку 29	α	№ строки	Схема по рисунку 29	α
	1.1			0,6
	1,2			0,7
	1,3			0,8
	1,4			0,9
	1,5			1,0
д	е		д	е

Участок ВА: 0 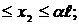Т₂ =

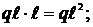
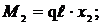
при x₂ = 0 M_В = 0; при х₂ = 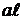М_А = q 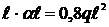(растянуты верхние волокна).

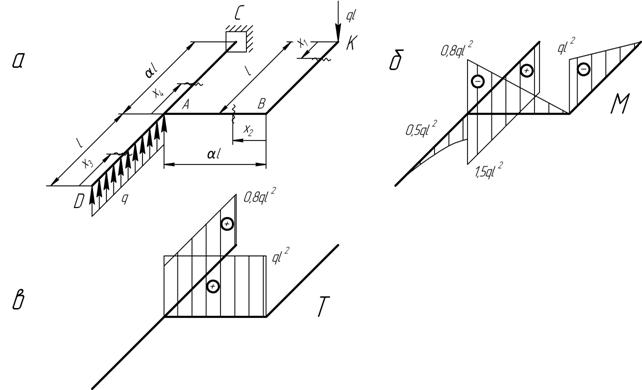
Рисунок 30 – Расчетная схема ломаного стержня и эпюры М и Т

Участок DA: 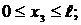Т₃ = 0; М₃ = q ;

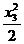при х₃ = 0 М_D = 0; при х₃ = 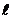М_A = q 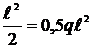(растянуты нижние волокна).

Участок АС: 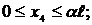Т₄ =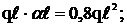

М₄ = ;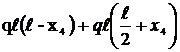

при х₄ = 0 М_А = q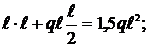

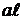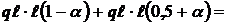при х₄ = М_С = 0,2 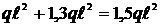(растянуты нижние волокна).

Эпюры внутренних силовых факторов, построенные по полученным выражениям, изображены на рисунке 30б, в.

2. По эпюрам внутренних силовых факторов установим, что опасными могут оказаться либо сечения участка АС (здесь все сечения равноопасны) с М = 1,5 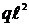и Т = 0,8q 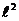, либо сечение, бесконечно близкое к точке А, принадлежащее участку АВ с М = 0,8q 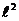и Т = q .

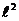Проверим оба эти сечения по четвертой теории прочности:

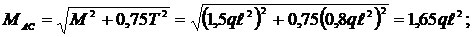
М = .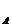

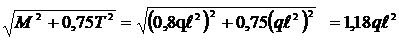Таким образом, наиболее опасными являются сечения участка АС с расчетным моментом М 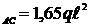.