Раздел 2. Аналитическая геометрия
Задания 21─30.Даны координаты вершин пирамиды А1, А2, А3, А4 . Найти:
1) площадь грани А1А2А3;
2) объем пирамиды;
3) уравнения прямой А1А2;
4) уравнение плоскости А1А2А3 ;
5) уравнение высоты А4D, опущенной из вершины А4 на грань А1А2А3 ;
6) длину высоты А4D;
7) координаты точки пересечения высоты А4D с плоскостью А1А2А3 .
21. А1 ( 4; 2; 5 ), А2 ( 0; 7; 2 ), А3 ( 0; 2; 7 ), А4 ( 1; 5; 0 ).
22. А1 ( 4; 4; 10 ), А2 ( 4; 10; 2 ), А3 ( 2; 8; 4 ), А4 ( 9; 6; 4 ).
23. А1 ( 4; 6; 5 ), А2 ( 6; 9; 4 ), А3 ( 2; 10; 10 ), А4 ( 7; 5; 9 ).
24. А1 ( 3; 5; 4 ), А2 ( 8; 7; 4 ), А3 ( 5; 10; 4 ), А4 ( 4; 7; 8 ).
25. А1 ( 10; 6; 6 ), А2 ( - 2; 8; 2 ), А3 ( 6; 8; 9 ), А4 ( 7; 10; 3 ).
26. А1 ( 1; 8; 2 ), А2 ( 5; 2; 6 ), А3 ( 5; 7; 4 ), А4 ( 4; 10; 9 ).
27. А1 ( 6; 6; 5 ), А2 ( 4; 9; 5 ), А3 ( 4; 6; 11 ), А4 ( 6; 9; 3 ).
28. А1 ( 7; 2; 2 ), А2 ( 5; 7; 7 ), А3 ( 5; 3; 1 ), А4 ( 2; 3; 7 ).
29. А1 ( 8; 6; 4 ), А2 ( 10; 5; 5 ), А3 ( 5; 6; 8 ), А4 ( 8; 10; 7 ).
30. А1 ( 7; 7; 3 ), А2 ( 6; 5; 8 ), А3 ( 3; 5; 8 ), А4 ( 8; 4; 1 ).
31. Прямые 2х + у – 1 = 0 и 4х – у – 11 = 0 являются сторонами треугольника, а точка Р( 1; 2 ) – точкой пересечения третьей стороны с высотой, опущенной на нее . Составить уравнение третьей стороны. Сделать чертеж.
32. Прямая 5х - 3у + 4 = 0 является одной из сторон треугольника, а прямые 4х - 3у + 2 = 0 и 7х + 2у – 13 = 0 его высотами. Составить уравнения двух других сторон треугольника. Сделать чертеж.
33. Точки А ( 3; -1 ) и В ( 4; 0 ) являются вершинами треугольника, а точка D ( 2; 1 ) - точкой пересечения его медиан. Составить уравнение высоты, опущенной из третьей вершины. Сделать чертеж.
34. Прямые 3х - 4у + 17 = 0 и 4х – у – 12 = 0 являются сторонами параллелограмма, а точка Р (2; 7 ) – точкой пересечения его диагоналей. Составить уравнения двух других сторон параллелограмма. Сделать чертеж.
35. Прямые х - 2у + 10 = 0 и 7х + у - 5 = 0 являются сторонами треугольника, а точка D ( 1; 3 ) ─ точкой пересечения его медиан. Составить уравнение третьей стороны. Сделать чертеж.
36. Прямые 5х - 3у + 14 = 0 и 5х - 3у – 20 = 0 являются сторонами ромба, а прямая х - 4у – 4 = 0 – его диагональю. Составить уравнения двух других сторон ромба. Сделать чертеж.
37. На прямой 4х + 3у – 6 = 0 найти точку, равноудаленную от точек А (1; 2 ) и В (- 1; - 4 ). Сделать чертеж.
38. Найти координаты точки, симметричной точке А (5;2 ) относительно прямой х + 3у – 1 = 0. Сделать чертеж.
39. Прямые х - 3у + 6 = 0 и 3х + у – 12 = 0 являются сторонами прямоугольника, а точка Р (7; 2 ) – точкой пересечения его диагоналей. Составить уравнения двух других сторон прямоугольника. Сделать чертеж.
40. Точки А (4;5) и С ( 2; - 1 ) являются двумя противоположными вершинами ромба, а прямая х – у + 1 = 0 – одной из его сторон. Составить уравнения остальных сторон ромба. Сделать чертеж.
Раздел 3. Введение в математический анализ
Задания 41─50.Вычислить пределы.
41. 1. 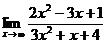 | 2. 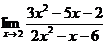 |
3. 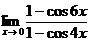 | 4. 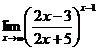 |
5. 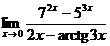 | |
42. 1. 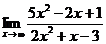 | 2. 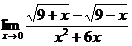 |
3. 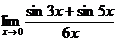 | 4. 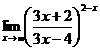 |
5. 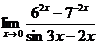 | |
43. 1. 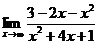 | 2. 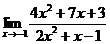 |
3. 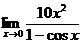 | 4.  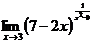 |
5. 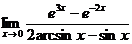 | |
44. 1. 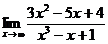 | 2.  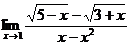 |
3. 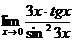 | 4. 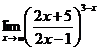 |
5. 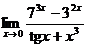 | |
45. 1. 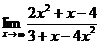 | 2. 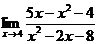 |
3. 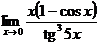 | 4. 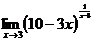 |
5. 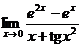 | |
46. 1. 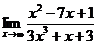 | 2. 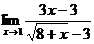 |
3. 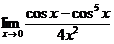 | 4. 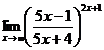 |
5. 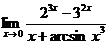 | |
47. 1. 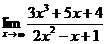 | 2. 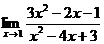 |
3. 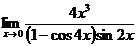 | 4. 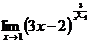 |
5. 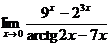 | |
48. 1. 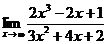 | 2. 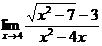 |
3. 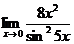 | 4. 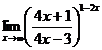 |
5. 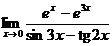 | |
49. 1. 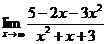 | 2. 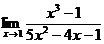 |
3. 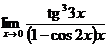 | 4. 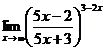 |
5. 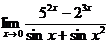 | |
50. 1. 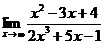 | 2. 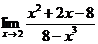 |
3. 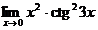 | 4. 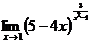 |
5. 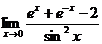 |
Раздел 4. Дифференциальное исчисление
Функции одной переменной
Задания 51─60.Найти производные 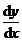 следующих функций:
следующих функций:
| 51. | |
1. 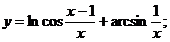 | 2. 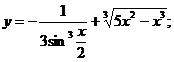 |
3. 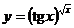 | 4. 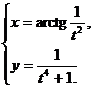 |
52.
1. 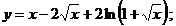 | 2. 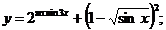 |
3. 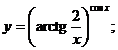 | 4. 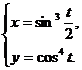 |
53.
1. 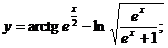 | 2. 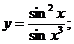 |
3. 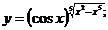 | 4. 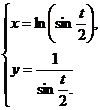 |
54.
1.  | 2. 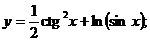 |
3. 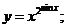 | 4. 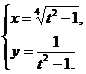 |
55.
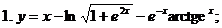 | |
2. 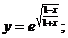 3. 3. 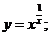 | 4. 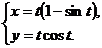 |
56.
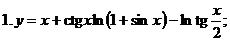 | |
2. 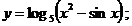 3. 3. 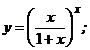 | 4. 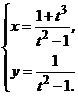 |
57.
1. 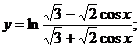 | 2. 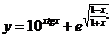 |
3. 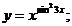 | 4. 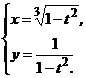 |
58.
1. 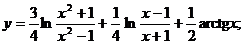 | |
2. 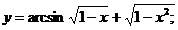 | |
3.  | 4. 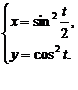 |
59.
1. 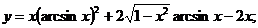 | |
2. 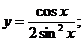 | |
3. 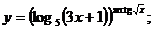 | 4. 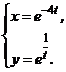 |
60.
1. 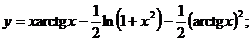 | |
2. 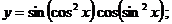 | |
3. 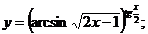 | 4. 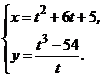 |
Раздел 5. Функции нескольких переменных
Задания 61─70.Найти частные производные первого порядка и указанную производную второго порядка от функции:
61. 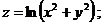 | 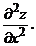 |
62. 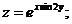 | 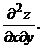 |
63. 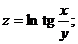 | 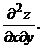 |
64. z = 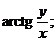 | 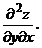 |
65. 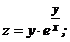 | 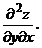 |
66. 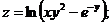 | 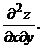 |
67. 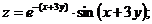 | 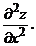 |
68. 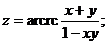 | 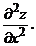 |
69. 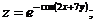 | 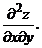 |
70. 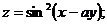 | 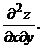 |
Задания 71─80.Дана функция 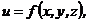 точка
точка 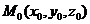 и вектор
и вектор 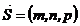 . Найти:
. Найти:
1) градиент функции в точке 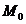 ;
;
2) производную функции в точке 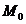 по направлению вектора
по направлению вектора 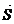 .
.
71. 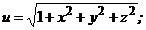 | 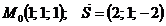 |
72. 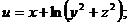 | 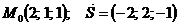 |
73. 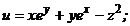 | 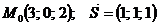 |
74. 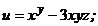 | 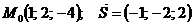 |
75. 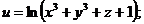 | 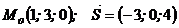 |
76. 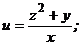 | 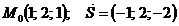 |
77. 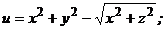 | 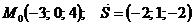 |
78. 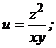 | 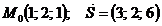 |
79. 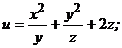 | 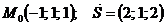 |
80. 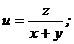 | 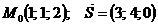 |
Раздел 6. Неопределенный интеграл
Задания 81─90.Найти неопределенные интегралы. В пунктах 1, 2 выполнить проверку дифференцированием.
81.
1. 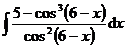 | 2. 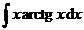 |
3. 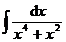 | 4. 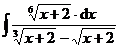 |
5. 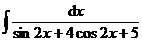 |
82.
1. 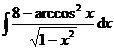 | 2. 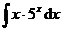 |
3. 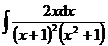 | 4. 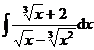 |
5. 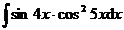 |
83.
1. 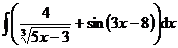 | 2. 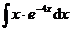 |
3. 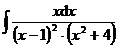 | 4. 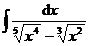 |
5. 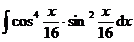 |
84.
1. 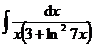 | 2. 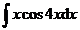 |
3. 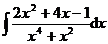 | 4. 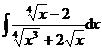 |
5. 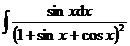 |
85.
1. 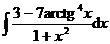 | 2. 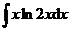 |
3. 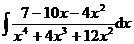 | 4. 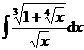 |
5. 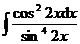 |
86.
1. 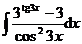 | 2. 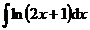 |
3. 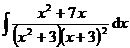 | 4. 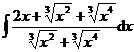 |
5. 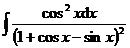 |
87.
1. 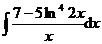 | 2. 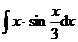 |
3. 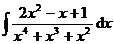 | 4. 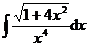 |
5. 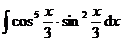 |
88.
1. 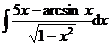 | 2. 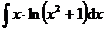 |
3. 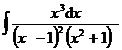 | 4. 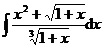 |
5. 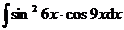 |
89.
1. 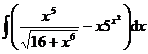 | 2. 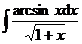 |
3. 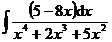 | 4. 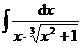 |
5. 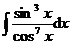 |
90.
1. 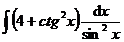 | 2. 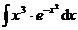 |
3. 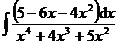 | 4. 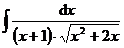 |
5. 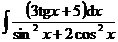 |
