Схема выбора, приводящая к перестановкам с повторениями
Изучение этого случая начнем с простого примера.
Сколько различных упорядоченных комбинаций можно составить из букв слова «музыка»? Сколько таких комбинаций можно составить из букв слова «огород»?
На первый вопрос ответ ясен – число комбинаций равно числу перестановок шести различных букв Р6 = 6! = 720. Во втором случае знакомая нам формула числа перестановок не может быть применена – буква «о» повторяется в слове три раза, и, меняя местами любые две буквы «о», мы не получим новой комбинации. Поэтому для ответа на второй вопрос нужно 720 разделить на число перестановок трех одинаковых букв «о», т.е. разделить на Р3 = 3! = 6. Значит, число различных комбинаций из букв слова «огород» - только 120.
В этом примере мы рассмотрели еще один тип выборок – перестановки с повторениями.
В предыдущих схемах мы изучали выборки из множества Е, которое содержало n различных элементов. Теперь рассмотрим множество F, состоящее из n элементов, которые не обязательно различны. Пусть первый элемент встречается в множестве F – n1 раз, второй – n2 раз, …, k-ый – nk раз, и n1+ n2 +… + nk = n.
Будем составлять различные перестановки элементов множества F, которые отличаются друг от друга порядком расположения элементов. Такие перестановки и называются перестановками с повторениями, а их общее число обозначается 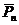 .
.
Выведем общую формулу для вычисления числа перестановок с повторениями. Если бы все элементы множества F были различными, то у нас получилось бы n! различных перестановок. Но т.к. некоторые элементы в множестве повторяются, и, меняя их местами, новой перестановки мы не получим, то понятно, что число перестановок с повторениями меньше n!. Остается дать ответ на вопрос – во сколько раз меньше?
Для ответа на этот вопрос нужно подсчитать, сколькими способами можно переставить одинаковые элементы. Элементы первого типа (в схеме это элементы а) можно переставить между собой 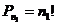 способами, второго типа –
способами, второго типа – 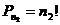 способами, k-го типа –
способами, k-го типа – 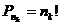 способами. При этом общее число перестановок с повторениями меньше n! в n1!·n2!·…·nk! раз, т.е. это число равно
способами. При этом общее число перестановок с повторениями меньше n! в n1!·n2!·…·nk! раз, т.е. это число равно 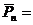
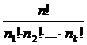 .
.
Часто при решении задачи приходится применять не одну, а несколько известных формул. Покажем это на примере следующей задачи.
Сколько различных перестановок из букв слова «огород» можно составить при условии, что три буквы «о» не стоят подряд?
Посчитаем сначала число перестановок букв в случае, когда три буквы «о» стоят рядом. В этом случае «ооо» можно считать за один символ. Остаются ещё три разных символа «г», «р» и «д». Всего четыре символа, поэтому перестановок может быть 4! = 24.
Для вычисления числа перестановок, в которых три буквы «о» не стоят подряд, достаточно от числа всех перестановок (это число получено в первом примере данного пункта и равно 120) вычесть число комбинаций, в которых три буквы «о» стоят рядом 120-24=96.
