Исследование функции с помощью производной: уравнения асимптот графика функции.

Прямая называется асимптотой графика функции, если расстояние от точек графика до этой прямой стремится к нулю при бесконечном удалении от начала координат вдоль графика функции. Асимптоты бывают вертикальные, наклонные и горизонтальные. Вертикальные асимптоты ищутся по точкам разрыва второго рода. Если в точке 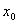функция терпит бесконечный разрыв, то вертикальная прямая 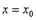является вертикальной асимптотой. График функции имеет наклонную асимптоту при 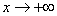(соответственно при 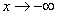), если существуют конечные пределы 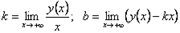(соответственно 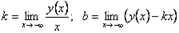). При этом уравнение наклонной асимптоты 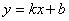. Если хотя бы один из двух пределов не существует (или бесконечен), то соответствующей наклонной асимптоты нет. 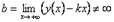Если и существует конечный предел , то асимптота является горизонтальной и её уравнение .

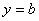8.Понятие о функции двух переменных. Область определения. Частные производные, полный дифференциал.

Понятие о функции двух переменных. Если указано правило, согласно которому с каждой точкой М плоскости сопоставляется некоторое число u, то говорят, что на плоскости «задана функция точки»; задание функции символически выражается равенством вида u=f(M). Число u, сопоставляемое с точкой М, называется значением данной функции в точке М. Функция двух переменных x и y обозначается символом f(x; y): если f(M)=f(x;y), то формула u=f(x; y) называется выражением данной функции в выбранной системе координат. Так, в предыдущем примере f(M)=AM; если ввести декартову прямоугольную систему координат с началом в точке А, то получим выражение этой функции: .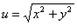

Область определения функции.Например функция z = f ( x, y ) двух переменных изобразится в виде некоторого множества точек на плоскости Oxy. Так, например, областью определения функции 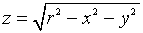является множество точек плоскости Oxy, координаты которых удовлетворяют соотношению 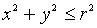т. е. представляет собой круг радиуса r с центром в начале координат.

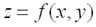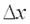Частные производные, полный дифференциал.Частной производной по х от функции называется предел отношения частного приращения этой функции по х к приращению , когда последнее стремится к нулю: 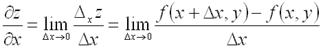.Частной производной по у от функции 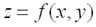называется предел отношения частного приращения этой функции по у к приращению 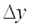, когда последнее стремится к нулю: 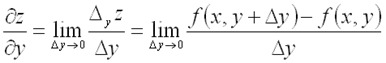.Пусть задана функция 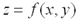. 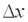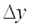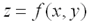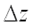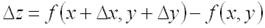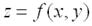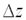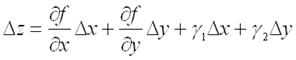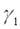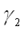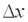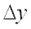Если аргументу х сообщить приращение , а аргументу у – приращение , то функция получит приращение , которое называется полным приращением функции и определяется формулой: .Функция , полное приращение которой в данной точке может быть представлено в виде суммы двух слагаемых : ,где и стремятся к нулю, когда и стремятся к нулю, называется дифференцируемой в данной точке.Линейная часть полного приращения функции называется полным дифференциалом и обозначается : 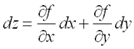,где 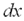и 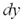– дифференциалы независимых переменных, которые, по определению, равны соответствующим приращениям и 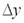.Частные производные от частных производных первого порядка называются частными производными второго порядка. Для функции двух переменных 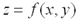их четыре: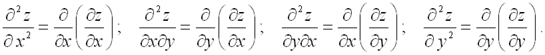

9.Функции N переменных. Область определения. Линии уровня. Кривые безразличия. Поверхности уровня. Предел. Непрерывность.

Переменная z называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.

Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у — ее аргументами.Обозначения: z = f(x,y), z = z(x,y).Замечание. Так как пару чисел (х,у) можно считать координатами некоторой точки на плоскости, будем впоследствии использовать термин «точка» для пары аргументов функции двух переменных, а также для упорядоченного набора чисел , являющихся аргументами функции нескольких переменных.

Переменная z (с областью изменения Z) называется функцией нескольких независимых переменных в множестве М, если каждому набору чисел из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.Обозначения: z = f, z = z.

Линии и поверхности уровня.Для функции двух переменных, заданной уравнением (1.1), можно рассмотреть множество точек (х,у) плоскости Оху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня.

Предел и непрерывность функции нескольких переменных.Введем понятие δ-окрестности точки М0 (х0 , у0) на плоскости Оху как круга радиуса δ с центром в данной точке. Аналогично можно определить δ-окрестность в трехмерном пространстве как шар радиуса δ с центром в точке М0 (х0 , у0 , z0). Для n-мерного пространства будем называть δ-окрестностью точки М0 множество точек М с координатами , удовлетворяющими условиюгде - координаты точки М0. Иногда это множество называют «шаром» в n-мерном пространстве.

Число А называется пределом функции нескольких переменных fв точке М0, если такое, что | f(M) — A| < ε для любой точки М из δ-окрестности М0.Необходимо учитывать, что при этом точка М может приближаться к М0, условно говоря, по любой траектории внутри δ-окрестности точки М0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых повторных пределов, получаемых последовательными предельными переходами по каждому аргументу в отдельности.

Функция f называется непрерывной в точке М0, если (1.2)Если ввести обозначения , то условие (1.2) можно переписать в форме (1.3).