Связь между дифференцируемостью и непрерывностью ф-ции.

Операция нахождения производной функции называется дифференцированием этой функции.

Функция 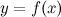имеет производную на интервале или называется дифференцируемой в этом интервале, если производная существует в каждой точке этого интервала.

Функция 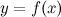имеет в точке бесконечную производную, если в этой точке .

Теорема: (О непрерывности функции в точке)

Если функция 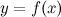имеет конечную производную в точке , то она непрерывна в этой точке.

Замечание. Обратное заключение не всегда верно: если функция 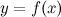непрерывна в некоторой точке , то она может и не иметь производной в этой точке.

Функция 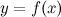называется дифференцируемой в точке , если приращение функции, соответствующее приращению аргумента, можно представить в виде:

где - число, не зависящее от , - б.м. функция при .

Теорема: (О необходимом и достаточном условии дифференцируемости)

Для того чтобы функция 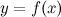была дифференцируемой в точке , необходимо и достаточно, чтобы 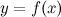имела в этой точке конечную производную.

Теорема устанавливает, что для функции 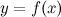дифференцируемость в данной точке и существование конечной производной в этой точке - понятия равносильные.

Основные правила дифференцирования. Таблица производных.

Логарифмическое дифференцирование.

Суть такого дифференцирования заключается в следующем: вначале находится логарифм заданной функции, а уже затем вычисляется от него производная. Пусть задана некоторая функция 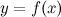. Прологарифмируем левую и правую части данного выражения:

функция имеет вид . Логарифмируем левую и правую часть:

далее по свойствам логарифма

Тогда

Производную в левой части равенства находим как производную сложной функции, а в правой - как производную произведения:

Производная сложной ф-ции.

Таблица производных сложных функций

Производная неявной ф-ции.

Если независимая переменная и функция связаны уравнением вида , которое не разрешено относительно , то функция называется неявной функцией переменной .

Всякую явно заданную функцию 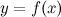можно записать в неявном виде . Обратно сделать не всегда возможно.

Несмотря на то, что уравнение не разрешимо относительно , оказывается возможным найти производную от по . В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию как функцию от , а затем из полученного уравнения найти производную .

Дифференциал ф-ции, св-ва. Его геометрический смысл.

Дифференциалом функции называется линейная относительно часть приращения функции. Она обозначается как или . Таким образом:

Геометрический смысл дифференциала

Дифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента .

Правило Лопиталя.

Теорема: (Правило Лопиталя).

Пусть функци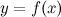и и удовлетворяют следующим условиям:

1) эти функции дифференцируемы в окрестности точки , кроме, может быть, самой точки ;

2) и в этой окрестности;

3) ;

4) существует конечный или бесконечный.

Тогда существует и , причем

Замечание: Правило Лопиталя распространяется на случай неопределенности типа при 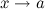. Правило Лопиталя распространяется и на случай . Чтобы убедится в этом, достаточно сделать замену и воспользоваться результатом выше приведенной теоремы. Иногда правило Лопиталя приходится применять несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы на каждом шаге должны оставаться справедливыми. Хотя правило Лопиталя работает только с неопределенностями и , неопределенности других типов могут быть раскрыты с его помощью, если путем преобразований удастся привести изучаемую неопределенность к указанному типу.