Виды уравнений плоскости в пространстве.

Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению:

Ax + By + Cz + D = 0, где А, В, С – координаты вектора 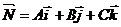-вектор нормали к плоскости.

Возможны следующие частные случаи:

А = 0 – плоскость параллельна оси Ох

В = 0 – плоскость параллельна оси Оу

С = 0 – плоскость параллельна оси Оz

D = 0 – плоскость проходит через начало координат

А = В = 0 – плоскость параллельна плоскости хОу

А = С = 0 – плоскость параллельна плоскости хОz

В = С = 0 – плоскость параллельна плоскости yOz

А = D = 0 – плоскость проходит через ось Ох

В = D = 0 – плоскость проходит через ось Оу

С = D = 0 – плоскость проходит через ось Oz

А = В = D = 0 – плоскость совпадает с плоскостью хОу

А = С = D = 0 – плоскость совпадает с плоскостью xOz

В = С = D = 0 – плоскость совпадает с плоскостью yOz

1. Уравнение плоскости, проходящей через три точки.

Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой. Рассмотрим точки М₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃) в общей декартовой системе координат.

Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М₁, М₂, М₃ необходимо, чтобы векторы 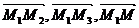были компланарны, т.е. ( 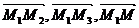) = 0

Таким образом,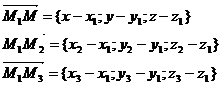

2. Уравнение плоскости, проходящей через три точки:

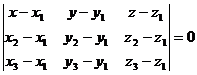
3. Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости.

Пусть заданы точки М₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂) и вектор .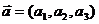

Составим уравнение плоскости, проходящей через данные точки М₁ и М₂ и произвольную точку М(х, у, z) параллельно вектору .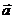

Векторы 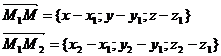и вектор 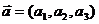должны быть компланарны, т.е.

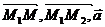( ) = 0. Уравнение плоскости:

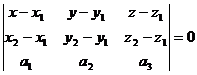
3. Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости.

Пусть заданы два вектора 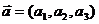и 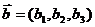, коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы 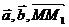должны быть компланарны. Уравнение плоскости:

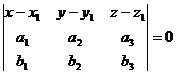
4. Уравнение плоскости по точке и вектору нормали.

Теорема. Если в пространстве задана точка М₀(х₀, у₀, z₀), то уравнение плоскости, проходящей через точку М₀ перпендикулярно вектору нормали 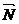(A, B, C) имеет вид: A(x – x₀) + B(y – y₀) + C(z – z₀) = 0.

Доказательство. Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор 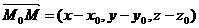. Т.к. вектор 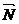- вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору 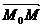. Тогда скалярное произведение

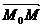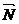× = 0. Таким образом, получаем уравнение плоскости

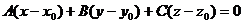
Теорема доказана.

5. Уравнение плоскости в отрезках.

Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на (-D)

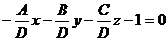, заменив 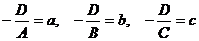, получим уравнение плоскости в отрезках:

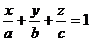
Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у, z.

6. Уравнение плоскости в векторной форме.

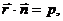где 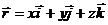- радиус- вектор текущей точки М(х, у, z), 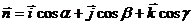- единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат; a, b и g - углы, образованные этим вектором с осями х, у, z; p – длина этого перпендикуляра.

В координатах это уравнение имеет вид:

xcosa + ycosb + zcosg - p = 0.

Теорема Ролля.

Теорема. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка e, a < e < b, в которой производная функция f(x) равная нулю,

f¢(e) = 0.

Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.

Доказательство. По свойству функций, непрерывных на отрезке функция f(x) на отрезке [a, b] принимает наибольшее и наименьшее значения. Обозначим эти значения М и m соответственно. Возможны два различных случая М = m и M ¹ m.

1. Пусть M = m. Тогда функция f(x) на отрезке [a, b] сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае за e можно принять любую точку интервала.

2. Пусть М = m. Так значения на концах отрезка равны, то хотя бы одно из значений М или m функция принимает внутри отрезка [a, b]. Обозначим e, a < e < b точку, в которой f(e) = M. Так как М- наибольшее значение функции, то для любого Dх ( будем считать, что точка e + Dх находится внутри рассматриваемого интервала) верно неравенство:

Df(e) = f(e + Dx) – f(e) £ 0

При этом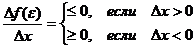

Но так как по условию производная в точке e существует, то существует и предел .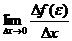

Т.к. 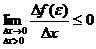и 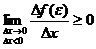, то можно сделать вывод: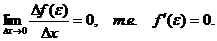

Теорема доказана.

Теорема Ролля имеет несколько следствий:

1) Если функция f(x) на отрезке [a, b] удовлетворяет теореме Ролля, причем

f(a) = f(b) = 0, то существует по крайней мере одна точка e, a < e < b, такая, что f¢(e) = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.

2) Если на рассматриваемом интервале (а, b) функция f(x) имеет производную (n-1)- го порядка и n раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная (n – 1) – го порядка равна нулю.

3. Вычислить координаты вектора 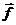, перпендикулярного вектору 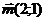, если .

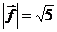Воспользуемся формулой скалярного произведения векторов:

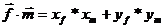
Так как векторы перпендикулярны, то 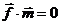. Получим систему уравнений:

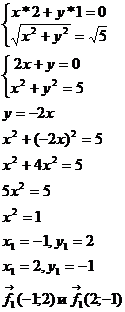
4. Вычислить .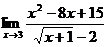

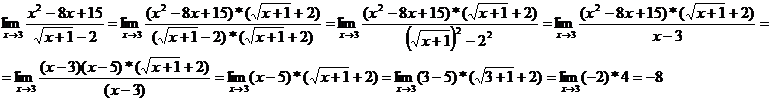
БИЛЕТ № 19.