Векторы. Координаты вектора. Скалярное произведение векторов.
Отрезок, для которого указано какой из его концов считается началом, а какой концом называется вектором. Направление вектора отмечается стрелкой. Любая точка пространства может тоже рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают и он не имеет какого-либо определенного направления.
Длиной ненулевого вектора 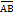 называется длина самого отрезка АВ. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора коллинеарны и если при этом их лучи сонаправлены, то такие векторы являются сонаправленными, а если эти лучи имеют противоположное направление, то они противоположно направленные. Ненулевой вектор сонаправлен с любым вектором.
называется длина самого отрезка АВ. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора коллинеарны и если при этом их лучи сонаправлены, то такие векторы являются сонаправленными, а если эти лучи имеют противоположное направление, то они противоположно направленные. Ненулевой вектор сонаправлен с любым вектором.
Единичный вектор – это вектор, длина которого равна единице. В пространственной системе координат существуют обозначения:  вектор оси абсцисс,
вектор оси абсцисс, 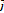 вектор оси ординат,
вектор оси ординат, 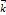 вектор оси аппликат. Все эти векторы называются координатными векторами. Любой вектор
вектор оси аппликат. Все эти векторы называются координатными векторами. Любой вектор  можно разложить по координатным векторам, то есть представить в виде
можно разложить по координатным векторам, то есть представить в виде 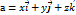 , причем различия определяются единственным образом.
, причем различия определяются единственным образом.
Свойства координат вектора:
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Каждая координата разности двух векторов равна разности соответствующих координат векторов
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Каждая координата вектора равна разности соответствующих координат его конца и начала.
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
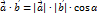
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Скалярный квадрат вектора равен квадрату его длины.
Длина вектора 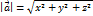
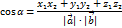
3.Найти наибольшее и наименьшее значение функции 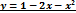 , заданной на отрезке
, заданной на отрезке 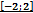 .
.
Билет №15
1.Применение производной к исследованию функций и построению графиков (на примере нахождения монотонности).
Производная помогает во многих случаях сравнительно просто исследовать функцию на монотонность.
Пусть функция y = f(x) определена и непрерывна в промежутке х и во всех внутренних точках этого промежутка имеет неотрицательную производную, причем равенство f’(x) = 0 выполняется не более чем в конечном числе точке этого промежутка. Тогда функция возрастает на промежутке х.
Пусть функция y = f(x) определена и непрерывна в промежутке х и во всех внутренних точках этого промежутка имеет положительную производную причем равенство f’(x) = 0 выполняется не более чем в конечном числе точек этого промежутка. Тогда функция y = f(x) убывает на промежутке х.
Для нахождения промежутков монотонности функции нужно:
Найти производную функции
Приравнять производную к нулю и решить уравнение
Отметить на числовой прямой корни уравнения
Определить знаки получившихся интервалов и записать ответ
