Векторы. Равенство векторов. Действия над векторами: сложение, вычитание векторов, умножение вектора на число.
Отрезок, для которого указано какой из его концов считается началом, а какой концом называется вектором. Направление вектора отмечается стрелкой. Любая точка пространства может тоже рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают и он не имеет какого-либо определенного направления.
Длиной ненулевого вектора 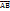 называется длина самого отрезка АВ. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора коллинеарны и если при этом их лучи сонаправлены, то такие векторы являются сонаправленными, а если эти лучи имеют противоположное направление, то они противоположно направленные. Ненулевой вектор сонаправлен с любым вектором.
называется длина самого отрезка АВ. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора коллинеарны и если при этом их лучи сонаправлены, то такие векторы являются сонаправленными, а если эти лучи имеют противоположное направление, то они противоположно направленные. Ненулевой вектор сонаправлен с любым вектором.
Векторы называют равными, если они сонаправлены и их длины равны. От любой точки можно отложить вектор, равный данному вектору и притом только один.
Отложит от какой-нибудь точки А вектор 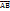 , из точки В вектор
, из точки В вектор 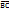 . Вектор
. Вектор 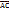 будет являться суммой векторов
будет являться суммой векторов 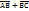 . Это правило сложения называется правилом треугольника. Для любых векторов
. Это правило сложения называется правилом треугольника. Для любых векторов 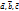 справедливо следующее:
справедливо следующее:
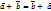
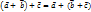
Разностью векторов 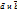 называется такой вектор, сумма которого с вектором
называется такой вектор, сумма которого с вектором  равна
равна  .
.
Произведение ненулевого вектора  на число ng w:val="EN-US"/></w:rPr><m:t>k</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
на число ng w:val="EN-US"/></w:rPr><m:t>k</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">  называется такой вектор
называется такой вектор  , длина которого |k|· |
, длина которого |k|· |  |, причем векторы
|, причем векторы  и
и  сонаправлены при k ≥ 0 и противоположно направлены при k < 0. Произведением нулевого вектора на любое число считается нулевой вектор. Для любого числа k и любого вектора а векторы а и ka коллинеарны.
сонаправлены при k ≥ 0 и противоположно направлены при k < 0. Произведением нулевого вектора на любое число считается нулевой вектор. Для любого числа k и любого вектора а векторы а и ka коллинеарны.
3.Найти производную третьего порядка для функции  .
.
Билет № 14
1.Применение производной к исследованию функций и построению графиков (на примере нахождения экстремумов).
Говорят, что функция y=f(x) имеет максимум и минимум в точке х = а, если у этой точки существует окрестность, в которой f(x)<f(a) (f(x)>f(a)) для х ≠ а. Точки максимума и минимума объединяют общим термином точки экстремума.
Если функция y=f(x) имеет экстремум в точке х = а, то либо f’(a)>0, либо f’(a) не существует. Это необходимое условие экстремума.
Точки, в которых f’(a)>0 называют стационарными, в точки в которых f’(a) не существует и которые принадлежат области определения функции называют критическими. Экстремумы функций могут достигаться только в стационарных или критических точках.
Пусть х = а стационарная или критическая точка функции y=f(x) и пусть существует интервал (b;c) соединяющий точку а внутри себя и такой, что на каждом из интервалов (b;a) и (a;c) производная f’(x) существует и сохраняет постоянный знак. Следует, что
Если на (b;a) производная y’ > 0, а на (а;с) производная y’< 0, то х = а точка максимума функции y = f(x)
Если на (b;a) производная y’ < 0, а на (а;с) производная y’> 0, то х = а точка минимума функции y = f(x)
Если на (b;a) и (а;с) производная y’ > 0 или y’< 0, то х = а не является точкой экстремума функции y = f(x). Это достаточное условие экстремума.
Чтобы найти экстремумы функции необходимо:
Найти производную функции
Приравнять производную к нулю и найти корни
Подставить полученные корни в функцию и просчитать
Выбрать точки максимума и минимума.
