Однофакторная линейная модель регрессии. Построение точечного прогноза и доверительного интервала.

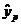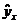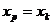В прогнозных расчетах по уравнению регрессии определяется предсказываемое значение как точечный прогноз при , т.е. путем подстановки в уравнение регрессии 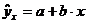соответствующего значения 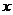. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки 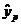, т.е. 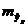, и соответственно интервальной оценкой прогнозного значения :

,

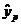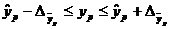где 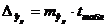, а 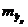– средняя ошибка прогнозируемого индивидуального значения:

.

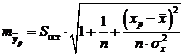Линейная многофакторная модель регрессии. Основные этапы построения модели.

1. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.

2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их. Проверить наличие мультиколлинеарности.

3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

4. С помощью 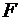-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации .

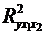5. С помощью t-критерия Стьюдента оценить статистическую значимость коэффициентов регрессии.

6. Доверительные интервалы для статистически значимых коэффициентов регрессии.

7. Доверительные интервалы для функции регрессии.

8. Доверительные интервалы для индивидуальных значений зависимой переменной.

9. С помощью частных 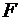-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора 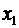после 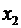и фактора 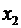после .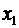

Корреляции для нелинейной регрессии. Средняя ошибка аппроксимации.

26. ?

27. ?

28. ?

Временные ряды. Основные задачи эконометрического исследования временного ряда.

Методы исследования моделей, основанные на данных пространственных выборов и временных рядов, отличаются друг от друга.

Это объясняется тем, что во временных рядах наблюдения нельзя считать независимыми.

Под временным (динамическим) рядом в эконометрике понимается последовательность наблюдений некоторого результативного признака У.

Эти наблюдения называются уровнями ряда:

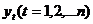- например, динамика курса акций и т.п.

В общем виде при исследовании временных рядов выделяется несколько составляющих:

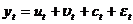- аддитивная модель

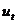- тренд (плавно меняющаяся компонента, описывающаяся чистое влияние долговременных факторов, т.е. длительную (вековую) тенденцию изменения результативного признака).

Под трендом понимают изменение, определяющее общее направление развития или основную тенденцию временного ряда.

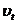- сезонная компонента, отражающая повторяемость …

- …

- …

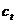Важнейшей задачей при исследовании временных рядов являются появление и статистическая оценка основной тенденции развития <…>.