Оценивание параметров линейной множественной модели регрессии.

Для оценки статистической значимости коэффициентов регрессии применяется t-критерий Стьюдента:

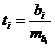
Стандартные ошибки вычислений параметров модели:

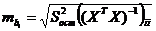
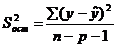
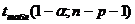
Если 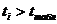– признается статистическая значимость коэффициента.

Коэффициенты β_j– показатель непосредственного влияния фактора Х_j на результат У.

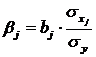, где ,

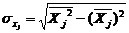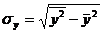
Стандартизованные β-коэффициенты показывают, на какую часть своего среднего квадратного отклонения 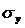изменится признак-результат У, с увеличением соответствующего фактора Х_j на величину своего среднего квадратного отклонения 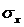, при неизменном влиянии прочих факторов модели.

Косвенное (апосредственное) влияние – влияние фактора на результат через другие факторы модели.

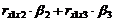
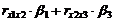
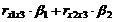
Δ_j- коэффициент характеризующий вклад j-ого фактора в суммарное влияние на результирующий показатель при условии независимости остальных факторов.

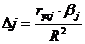
17. ?

18. ?

19. ?

Оценка влияния отдельных факторов на результативный показатель по коэффициентам детерминации и эластичности.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором, при элиминировании (устранении влияния) других факторов, включённых в уравнение регрессии.

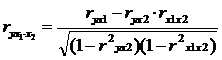
Коэффициенты эластичности позволяют ранжировать факторы по силе влияния фактора на результирующий признак.

Частный коэффициент эластичности показывает насколько процентов в среднем изменяется результирующий признак при увеличении фактора Х_i на 1% от своего среднего уровня, при фиксированном положении других факторов модели.

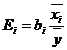
Понятие об эконометрических моделях. Отличие эконометрических моделей от математических моделей. Спецификация и идентификация моделей.

Математически уравнение регрессионной связи записывается следующим образом:

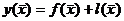
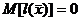
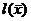- остаточная составляющая (регрессионные остатки).

Однофакторная линейная модель регрессии. Определение параметров модели по МНК.

Построение линейной регрессии сводится к оценке ее параметров – 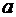и 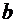. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров 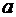и 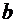, при которых сумма квадратов отклонений фактических значений результативного признака 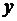от теоретических 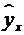минимальна:

.

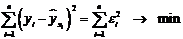Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной.

Как известно из курса математического анализа, чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров 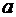и 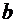и приравнять их к нулю. Обозначим 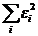через 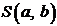, тогда:

.

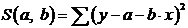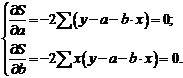
После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров 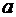и :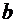

, ,
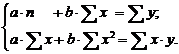
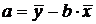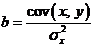