Минимизация булевых выражений по картам Карно. (2)

`А`В `А В А В А`В

`С`D 1₁ 1₂ B`C

`C D 1<sub>3</sub> 1<sub>4</sub> `A C`D

C D

C`D 1₅ 1₆

F1 = B C + `A C`D

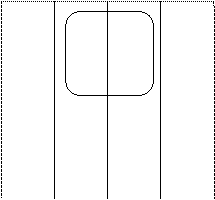
Рис.4.10.2. Пример минимизации булевой функции F1 с помощью карты Карно для 4–х переменных.

В первом примере минимизации булевой функции F1 нижний контур из двух единиц 1₅ и 1₆ , соответствующие пятому и шестому слагаемым в исходном булевом выражении, дает возможность опустить B и`B. После этого в нем остается произведение `A C`D. В верхнем контуре из четырех единиц 1<sub>1</sub>, 1<sub>2</sub>, 1<sub>3</sub> и 1<sub>4</sub> , соответствующие первым четырем слагаемым в исходном булевом выражении попарно опускаются A и`A, D и`D, так что в результате этого верхний контур дает произведение B C.

2.F2 =`А`В`С`D₁ +`A B`C`D<sub>2</sub> + A B`C`D<sub>3</sub> +`A`B C`D₄ +`AB C`D₅

`А`В `А В А В А`В

`С`D 1₁ 1₂ 1₃ B`C`D

`C D `A`D

C D

C`D 1₄ 1₅

F2 =`A`D + B`C`D

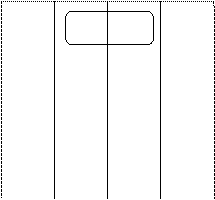
Рис.4.10.3. Пример минимизации булевой функции F2 с помощью карты Карно для 4–х переменных.

Во втором примере минимизации булевой функции F2 контур из двух единиц 1₂ и 1₃ , соответствующие второму и третьему слагаемым в исходном булевом выражении, дает возможность опустить А и`А. После этого в нем остается произведение B`C`D. В контуре из четырех единиц 1<sub>1</sub>, 1<sub>2</sub>, 1<sub>4</sub> и 1<sub>5</sub> , соответствующие другим четырем слагаемым из исходного булева выражения, попарно опускаются В и`В, С и`С, так что в результате этого верхний контур дает произведение `A`D. Карта Карно представляется в данном случае свернутой в цилиндр, в котором верхний край совмещается с нижним.

Этот пример показывает также, что контуры могут накладываться друг на друга.

Билет 3

2)3.Мультиплексор. Определение, условное графическое обозначение, схема и таблица истинности.

Мультиплексированием (MULTIPLEX) называют передачу данных от нескольких источников по одному каналу поочередно. В качестве примера перекличка студентов на лекции – передача данных от каждого студента по спискам групп через преподавателя в журнал. Обратный процесс – из журнала через декана некоторые студенты получат данные – это демультиплексирование.

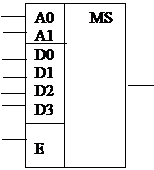
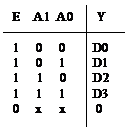
В цифровой технике мультиплексор имеет m информационных входов данных D0,D1,D2,D3,…,D_m; n адресных входов А1,А2,А3,…,А_n; и один выход данных. m=2ⁿ

Двоичный код на входах адреса определяет номер того входа данных, с которого информация проходит на выход MS в этот момент. Обозначения MS отличается от MUX, которого требует ГОСТ, потому что в нем отражена еще одна функция – выборка, селекция данных из определен-

ного, указанного адресом источника, которая обозначается

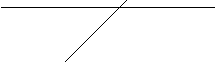
SL-SELECT – выбирать. Обозначение MS встречается чаще всего, но иногда бывает MUX , и изредка SL

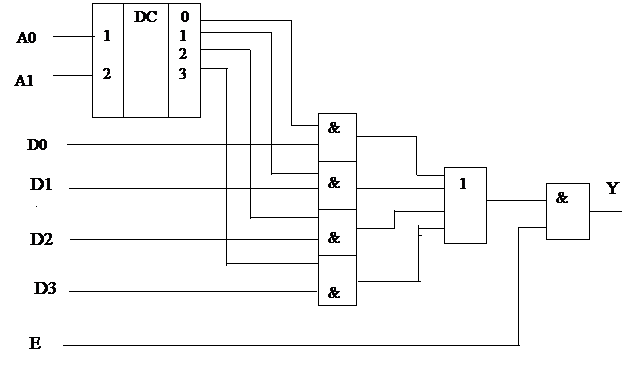
В состав мультиплексора обязательно входит дешифратор адреса в том или ином виде. В первом варианте мультиплексора дешифратор адреса выделен в отдельный узел.

Как известно линейный дешифратор состоит из групы инверторов по адресным входам и линейки – столбца – элементов И.

Столбец элементов И мультиплексора может выполнять функцию линейного дешифратора , если эти элементы И, но с большим числом входов подключить к выходам инверторов по адресным линиям в соответствии с таблицей истинности дешифратора.

Второй вариант схемы мультиплексора , полученный с учётом вышеизложенного , считается минимизированным в базисе И-НЕ. Так построен мультиплексор К155КП2.

Билет 4

1) Различия между позиционными и непозиционными системами счисления.

Все современные системы счисления (кроме некоторых римских цифр) являются позиционными, т.е. в них одна и та же цифра в разных позициях (слева, справа) имеет разное значение. Например в десятичном числе 55 левая цифра означает 50, а правая – только 5. В общем виде в позиционной системе счисления с основанием системы Х число А можно представить в виде:

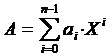
где n – количество разрядов числа А, а_i – коэффициенты каждого разряда, которые могут принимать значения от 0 до Х – 1.

При необходимости основание системы счисления указывается внизу после числа в виде нижнего индекса.

ПРИМЕРЫ:

1. Четырехразрядное десятичное число:

5685₁₀ = 5×10³ + 6×10² + 8×10¹ + 5×10⁰ ,

где Х = 10 – основание системы счисления, а₀ = 5, а₁ = 8, а₂ = 6,

а₃ = 5 – коэффициенты в каждом разряде, n = 4 – количество разрядов числа А.

2. Трехразрядное восьмеричное число:

372₈ = 3×8² + 7×8¹ + 2×8⁰ = 106₁₀

где Х = 8 (восьмеричная система счисления), коэффициенты в разрядах числа A а₀ = 2, а₁ = 7, а₂ = 3; n = 3 – количество разрядов числа А.

3. Двухразрядное шестнадцатеричное число:

4E₁₆ = 4×16¹ + 14×16⁰ = 78₁₀

где Х = 16 (шестнадцатеричная система счисления), коэффициенты в разрядах числа А а₀ = E = 14, а₁ = 4 (шестнадцатеричные цифры от 0 до 9 записываются так же, как и соответствующие десятичные цифры, а шестнадцатеричные цифры 10,11,12,13,14,15 записываются заглавными латинскими буквами А,В,С,D,Е,F соответственно); n = 2 – количество разрядов числа А.

4. Четырехразрядное двоичное число:

1101₂ = 1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 13₁₀

где X = 2 – двоичная система счисления, коэффициенты в разрядах числа А а₀ = 1, а₁ = 0, а₂ = 1, а₃ = 1, n = 4 – количество разрядов числа А.

Двоичную цифру, которая может принимать только два значения: 0 или 1, называют "бит", происходящее от сокращения BIT английских слов BI NARY DIGI T – "двоичная цифра".

Десятичная система, к которой мы привыкли, основана на количестве пальцев рук и для применения в цифровой технике неудобна. В цифровой аппаратуре устройства обычно имеют два рабочих состояния и в них применяют двоичную систему счисления. Восьмеричная и шестнадцатеричная системы счисления являются как бы компромиссными между двоичной и десятичной системами счисления и применяются в вычислительной технике из–за удобства представления больших двоичных чисел.

Билет4