Матрица, её строчный и столбцовый ранги

Матрицей над F называется прямоугольная таблица элементов этого поля.

Пусть 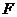– поле. Таблица вида

,

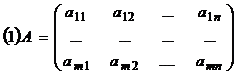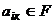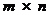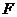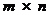где , называется матрицей размера над полем или - матрицей над 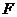. Скаляры 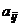называются элементами матрицы. Краткая запись: 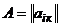. Множество всех 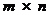матриц обозначается .

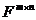Введем следующие обозначения для строк и столбцов матрицы: 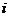-я строка матрицы обозначается через 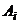, 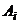= 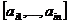; 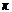-й столбец матрицы обозначается через

.

Строки матрицы 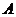можно рассматривать как 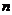-мерные арифметические векторы над 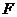. Столбцы матрицы 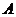можно рассматривать как 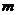-мерные векторы над .

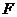Определение 1: Строчечным рангом матрицы 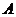называется ранг системы ее строк 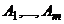, рассматриваемых как 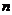-мерные векторы над 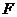. Столбцовым рангом матрицы 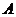называется ранг системы ее столбцов 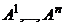, рассматриваемых как 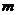-мерные векторы над .

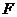Строчечный ранг матрицы 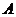обозначается через 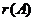, столбцовый ранг матрицы 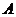обозначается через .

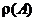Строчечный ранг – одна из важнейших характеристик матрицы. Рассмотрим один из способов вычисления строчечного ранга матрицы. Для этого рассмотрим элементарные преобразования матрицы. К элементарным преобразованиям относятся следующие действия над строками:

а) вычеркивание нулевой строки;

б) прибавление к одной из строк другой строки, умноженной на любое число;

в) перестановка двух строк.

Теорема 1: Строчечный ранг матрицы не меняется при элементарных преобразованиях.

Доказательство: Рассмотрим по отдельности каждый из типов элементарных преобразований. Совершенно очевидно, что перестановка строк не меняет линейных зависимостей между строками матрицы, поэтому для преобразований типа в) утверждение теоремы справедливо.

Несложно показать справедливость теоремы и для преобразования а).

Пусть над матрицей 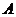выполняется преобразование б): к строке 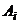прибавляется строка 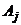, умноженная на число 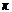. Рассмотрим две системы векторов: 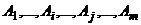(1) и 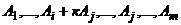(2). Легко видеть, что их линейные комбинации состоят из одних и тех же векторов: 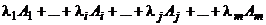и 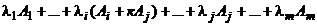. Поэтому максимальное число линейно независимых векторов в системе (1) и (2) будет совпадать. Таким образом, строчечный ранг матрицы при преобразовании а) не меняется . Теорема доказана.

Из этой теоремы вытекает метод вычисления строчечного ранга матрицы. Идея метода заключается в том, что при помощи элементарных преобразований, мы приводим данную матрицу к специальному виду, который называется ступенчатым, а после этого сразу же написать 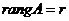или 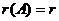, если в ступенчатой матрице 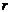строк.

, , .

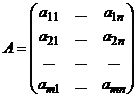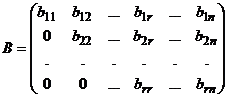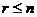В самом деле, система всех строк матрицы 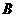линейно независима, поэтому ранг этой матрицы равен числу её строк, т.е. 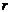. Учитывая, что ранг не меняется при элементарных преобразованиях, имеем: .

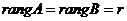Проверить самостоятельно, что система векторов строк матрицы 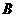линейно независима.

Пример: ,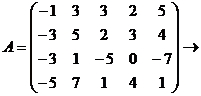

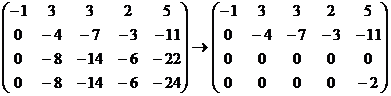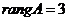
Определение 2: Матрица, получающаяся из матрицы 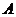в результате замены её строк соответствующими столбцами этой матрицы, называется транспонированной к 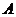и обозначается :

.

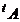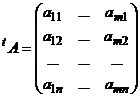Символам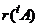и и 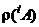обозначаются соответственно строчный и столбцовый ранги матрицы .

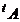Теорема 2:Строчный ранг матрицы равен её столбцовому рангу.

Без доказательства.