Физический, геометрический и экономический смысл производной.

Физический смысл:

f’(x) – есть мгновенная скорость в точке х₀ процесса, описываемого f(x).

Экономический смысл:

Если f(x) описывает экономический процесс, то f’(x) – предельная характеристика этого процесса в точке х₀.

Дифференцируемойназывается функция f(x), если она имеет производную в точке х₀

Функция f(x) называется замкнутой на [a,b], если она дифференцируема на (a,b) и в точке х = а справа, в точке х=bслева.

Теорема1. Если f(x) дифференцируема в точке х₀, то она непрерывна в этой точке. Обратное не выполняется.

Геометрический смысл производной:

y’(x)=tga, где a - угол между касательной, проведенной к функции в точке х₀ с осью О_х.

Уравнение касательной:

у-у0=f’(x0)(x-x0)

Матрица А в соотношении 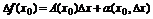называется производной или матрицей Якоби и обозначается f’(x₀), Df(x₀), .

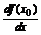Дифференциалфункции f(х) – главная линейная часть относительно Dу.

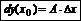
Дифференцирование функции – процесс отыскания производной.

Теорема о дифференциале. Для того, чтобы в точке Х0 существовал дифференциал f(x), необходимо и достаточно, чтобы в этой точке существовала производная.

!В линейной функции дифференциал и приращение совпадают.

Свойство инвариантности (отличия) dy состоит в том, что дифференциал простой и сложной функции по виду одинаковые.

Таблица производных.

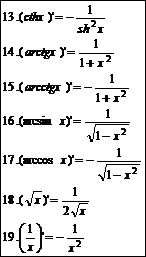
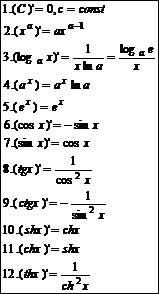
Частная производная функции f(x₁,x₂,…,x_n) по переменной х₁ – предел

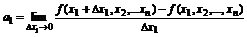, обозначается:

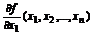
Смешанные частные производные – частные производные, в которые входит дифференцирование по различным переменным.

Правило дифференцирования:

Пусть функция v(x) и u(x) дифференцируемы в точке х, тогда в этой точке существует производная.

Свойства производных:

1. (u(x)±v(x))’=v’(x)±v’(x)

2. (u(x) v(x))’=u’(x)*v(x)+v’(x)*u(x)

3.

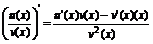
Правило дифференцирование обратной функции:

Обратная функция x = f^-1– функция, заданная неявно уравнением f(x)-y =0.

Если у=f(x) монотонная функция, то существует x=j(y) на Y.

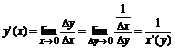
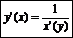
Производная сложных функций.

Теорема. Если y=f(x), а d(y) = z, и функция f дифференцируема в точке х, а функция d дифференцируема в точке f(x), то композиция отображений y 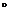d дифференцируема в точке х и

(y 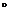d)’ = (y’ 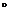d) d или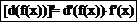

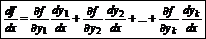
где f=f[y₁(x),y₂(x),…y_k(x)].

26. Производная сложной функции.

Производная сложной функции:

Пусть функция y=f(u) (где u=j(x)) - дифференцирована в точке х₀, а y=f(x) – в точке u₀=j(x₀), тогда f(j(x)) – дифференцированы в точке х₀ и:

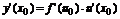
Производная высшего порядка.

Производная высшего порядка – производная от одной или нескольких производных.

Дифференцирование функций, заданных неявно.

Говорят, что функция y= f(x), xÎ (a,b), неявно задана уравнением F(x,y)=0, если для любого числа х (который принадлежит интервалу (a,b) ) выполняется равенство: F(x, f(x))=0.

Для вычисления производной функции y= f(x) надо продифференцировать тождество F(x, f(x))=0 по х (рассматриваем левую часть как сложную функцию х), а затем полученное уравнение решить относительно f’(x).