Класс основных элементарных функций.

Степенная функция х^l, где lÎR

Показательная функция ax, а>0,a¹1.

Логарифмическая функция logax,a>0, a¹1.

Тригонометрические функции sinx, cosx, tgx, ctgx.

Обратные тригонометрические функции arcsinx, arccosx, arctgx, arcctgx.

Часто используются функции

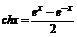- гиперболический синус

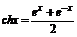- гиперболический косинус

Суперпозиция (композиция отображений)

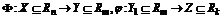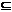Пусть и Y Y₁. Отображение f: X 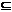R_n®Z 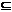R_k называется суперпозицией (композицией) отображений y и Ф и обозначается f=y 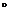Ф, если для любого х из Х имеет место соотношение f(x) = (y Ф)х = y (Ф(х)).

Переменная у=Ф(х) называют промежуточной переменной или промежуточным аргументом.

Системы окрестностей

Окрестностью точки х₀ из R называется любой интервал (a,b), содержащий эту точку.

Частные виды окрестностей:

Симметричная Ud(x₀) точки х₀ радиусом d>0,

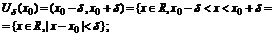
Проколотая окрестность – окрестность U(x0), из которой удалена точка х₀, U(x₀)={xÎR, a<x<b, x¹x₀)};

Симметричная проколотая окрестность: Ud(x₀)={xÎR, 0<|x-x₀|<d}.

Окрестностью бесконечно удаленной точки 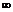в R (U ( 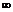)) называется внешность некоторого отрезка, т.е. множество точек, не принадлежащих этому отрезку.

Симметричной окрестностью точки 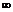называется внешность симметричного относительно нуля отрезка.

Окрестностью бесконечно удаленной точки в R_n(U ( 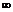)) называется внешность шара с центром в начале координат либо внешность n – мерного куба, симметричного относительно начала координат.

Предельная точка (точка сгущения) – точка М₀, множества Х, если в любой ее окрестности есть хотя бы одна отличная от М₀ точка множества Х.

Внутренняя точка множества Х– точка М₀ÎХ, входящая в множество Х вместе с некоторой окрестностью.

Граничная точка М₀ множества Х – такая точка, в окрестности которой есть точки как принадлежащие Х, так и не принадлежащие ему.

Предел последовательности (определение Коши)

Пределом последовательности X_n называют число А, если для любого сколько угодно малого е >0 существует N (е) такой, начиная с которого (n>N) выполняется неравенство |x_n-А|< е

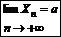
Предел векторной последовательности {y_n} – вектор (точка) А (принадлежащая пространству R_n), при которой для любой окрестности U существует окрестность V такая, что для всех n, (принадлежащих окрестности V) последовательность y_n принадлежит (U).

Теорема1. Для того, чтобы последовательность

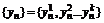точек (векторов) пространства R_k сходилась к точке (вектору) А=(А₁, А₂, …А_k), Û чтобы каждая координатная последовательность 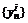сходилась и при этом ( ).

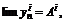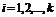Теорема2. Всякая монотонно возрастающая (убывающая) и ограниченная сверху (снизу) числовая последовательность имеет предел.

Теорема3. Если даны три числовых последовательности un,vn,bn, удовлетворяющие условию u_n£ b_n £ v_n и 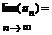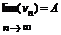, то и

lim w_n=A.