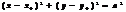Производная 2го порядка ф-ции нескольких переменных. Дифференцирование сложной ф-ции 2х переменных.

Частное производной 2го порядка от ф-ции Z явл. частная производная от 1й производной:

Z``<sub>XX</sub>=(Z`<sub>x</sub>)`<sub>x</sub> ; Z``_yy=(Z`<sub>y</sub>)`_y

Z``_Xy=(Z`<sub>x</sub>)`_y=(Z`<sub>y</sub>)`_x

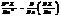
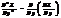
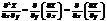
Экстремумы ф-ции несколькихпеременных. Необходимые и достаточные

Признаки экстремума ф-ции 2х переменных.

Z=f(x,y), M₀(x₀,y₀), M(x,y)

Max ф-ции Z называется такое ее значение f(x₀,y₀), которое является наибольшим среди всех значений, принимаемых в некоторой окрестности точки M₀

Min ф-ции Z называется такое ее значение f(x₀,y₀), которое является наименьшим среди всех значений, принимаемых в некоторой окрестности точки M₀

Экстремум сущ. в тех точках, в которых частная производная ф-ции Z=0 или не существует:

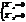
Если Z=f(x₁,x₂,...x_n), то ¶Z/¶x_i=0, i=1,2,...n - необходимое условие.

Достаточный признак:

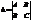
где A= Z``<sub>XX</sub>(x<sub>0</sub>,y<sub>0</sub>), C= Z``_yy(x₀,y₀), B= Z``_yx (x₀,y₀),

1) если D>0, то М₀ - точка экстремума;

если А<0 или С<0, то М₀ - точка max;

если А>0 или С>0, то М₀ - точка min.

2) если D<0, то экстремума нет

3) если D=0, то вопрос о существовании экстремума остается открытым.

Общая схема исследования ф-ции необходима для построения графика.

Найти:
-обл. определения ф-ции

-точки разрыва и интервалы, где ф-ция явл-ся непрерывной

-поведение ф-ции в окрестностях точки разрыва, вертикальной асимптоты

-т. пересечения графика с осями координат

-симметрия графика (чет./нечет):

f(-x)=x симметрична относительно осей

f(-x)=-x симметрична относительно О(0,0)

-периодичность

-интервалы монотонности

-точки экстремума

-наибольшее и наименьшее значение

-выпуклость, вогнутость

-точки перегиба

-поведение ф-ции в безконечности, наклонная и горизонтальные асимптоты

-нанесение на график.

Теоремы о среднем. Правило Лопиталя.

Рассмотрим способ раскрытия неопределенностей 0 / 0 и ∞ / ∞, который основан на применении производных.

Правило Лопиталя, при 0 / 0.

Пусть функции f(x) и φ(x) непрерывны и дифференцируемы в окрестности точки x₀ и обращается в нуль в этой точке: .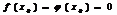

Пусть φ ′(x) ≠ 0 в окрестности точки x₀

Если существует предел

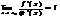,то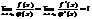

Применим к функциям f(x) и φ(x) теорему Коши для отрезка [x₀;x], лежащего в окрестности точки x₀ , тогда

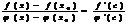, где с лежит между x₀ и х.

При x→x₀ величина с также стремится к х₀; перейдем в предыдущем равенстве к пределу:

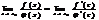
Так как 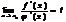, то .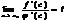

Поэтому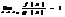

(предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует)

Правило Лопиталя, при ∞ / ∞.

Пусть функции f(x) и φ(x) непрерывны и дифференцируемы в окрестности точки x₀ (кроме точки x₀), в этой окрестности

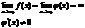
Если существует предел

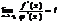, то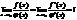

Неопределенности вида 0∙∞ ; ∞-∞ ; 1^∞ ; ∞⁰ ; 0⁰ сводятся к двум основным.

Например, 0∙∞

Пусть f(x)→0, φ(x)→∞ при х→х

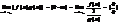
Теорема Ферма.

y=f(x) определена на [a;b] в некотор т. x=cЄ [a;b] a-ция принимает наибили наим знач, если сущ f `(x) то f `(x)=0

доказ-во: f `(c)=lim(f(c+∆x)-f(c))/∆x x=с – наиб

(x→x0)

знач ∆x f(c+∆x)-f(c) >=0

a) при ∆x<0 f `(с) lim(f(c+∆x)-f(c))/∆x<=0

(x→x0)

б) при ∆x>0 f `(с) lim(f(c+∆x)-f(c))/∆x>=0

(x→x0)

f `(c)<=0 → f `(c)=0

f `(c)>=0 →

геометрич смысл: если в некотр т. ф-ция примант наиб знач и производная сущ, то касат графика ф-ции ║оси x

Прямая на поскости

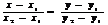
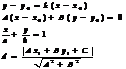
Прямые 2-ого порядка

Эллипс

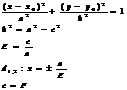
Гипербола

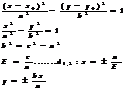
Парабола

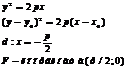Окружность