Точек перегиба и участков выпуклости и вогнутости функции

1) Сначала находятся критические точки второго рода, т.е. точки, в которых вторая производная равна нулю или не существует.

2) Затем область определения функции разбивается на интервалы критическими точками и точками разрыва функции и определяется знак второй производной 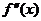в каждом из полученных интервалов (для чего достаточно определить знак 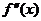в какой-либо одной точке каждого интервала). Если при переходе через эти точки вторая производная меняет знак, то эти точки являются точками перегиба функции, если смены знака второй производной не происходит, то точки не являются точками перегиба. При этом на тех интервалах, где 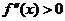, функция выпукла вниз, где 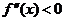, – выпукла вверх.

Порядок действий при этом рекомендуется следующий.

1. Найти область определения функции.

2. Найти .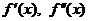

3. Определить критические точки второго рода и пронумеровать их в порядке возрастания.

4. Составить таблицу II.

	Интервалы выпуклости, вогнутости и к. т. II
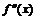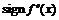	на интервалах и поведение в к. т. II
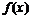	Поведение графика функции на интервалах выпуклости, вогнутости и значение функции в к. т. II

Пример 6. Найти интервалы выпуклости, вогнутости и точки перегиба функции .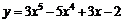

1. ▲ Областью существования функции является весь бесконечный интервал .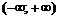

2. Найдем производные: .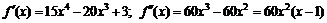

3. Вторая производная существует при всех и равна нулю 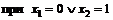. Критическая точка II рода 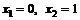. Разобьем область определения функции на интервалы 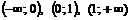и определим знак в каждом из них. Для этого достаточно определить знак в какой-либо одной точке интервала. Удобно взять точки .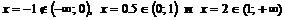

Так как 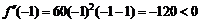, то на интервале 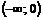функция выпукла вверх;

так как 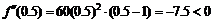, то на интервале 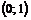функция выпукла вверх;

так как 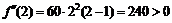, то на интервале 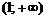функция выпукла вниз.

Вторая производная равна нулю 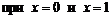. При переходе через точку 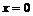вторая производная не меняет знак, следовательно, в точке 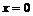функция перегиба не имеет. При переходе через точку 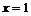вторая производная меняет знак, следовательно, в точке 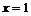функция имеет перегиб.

4. Составим таблицу II.

						▼
	–		–		+
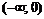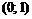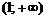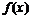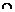		Нет т. п.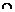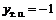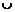

Замечание. Условимся в дальнейшем выпуклость вверх и выпуклость вниз графика в таблице обозначать так: .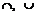

Пример 7. Найти интервалы выпуклости, вогнутости и точки перегиба функции .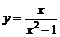

1. ▲ Область определения функции .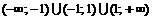

2. Найдем производные: ,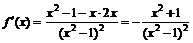

.

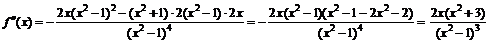3. Вторая производная не существует 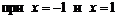и равна нулю. Вторая производная равна нулю 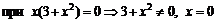. Единственная критическая точка второго рода 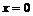, так как точки 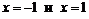области определения не принадлежат. Разобьем область определения функции на интервалы .

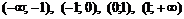4. Составим таблицу II, знак второй производной на интервалах выпуклости и вогнутости определить по ее знаку в произвольной точке интервалов.

						▼
	–	+		–	+

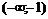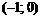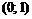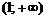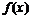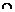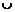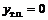Пример 8. Найти интервалы выпуклости, вогнутости и точки перегиба функции .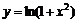

1. ▲ Область определения функции .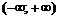

2. Найдем производные: .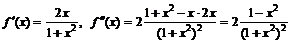

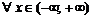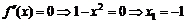3. Вторая производная функции существует . и 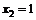. Критические точки второго рода 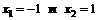. Разобьем область определения функции на интервалы .

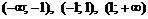4. Составим таблицу II, знак второй производной на интервалах выпуклости и вогнутости определить по ее знаку в произвольной точке интервалов.

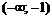		–1				▼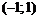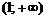
	–		+		–

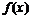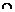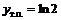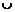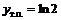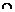Пример 9. Найти интервалы выпуклости, вогнутости и точки перегиба функции .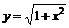

1. ▲ Область определения функции .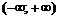

2. Найдем производные:

, .

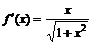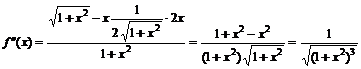3. Вторая производная функции существует 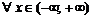. Вторая производная 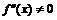. Критических точек второго рода нет, поэтому нет точек перегиба (не выполнен необходимый признак). Так как 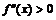, то график функции выпуклый вниз. ▼

АСИМПТОТЫ ГРАФИКА ФУНКЦИИ

Может оказаться, что размеры графика данной функции 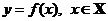, не ограничены. Это бывает, когда функция не ограничена или когда она задана на неограниченном промежутке. В таких случаях часто представление о графике функции вне рамок чертежа дают асимптоты графика.

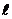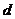Определение. Прямая называется асимптотой кривой , если расстояние от точки 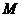кривой до прямой 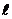стремится к нулю при неограниченном удалении точки 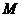по какой-либо части кривой от начала координат.

Различают три вида асимптот: вертикальные (параллельные оси 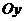), горизонтальные (параллельные оси 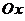) и наклонные (не параллельные ни одной из координатных осей).

Прямая 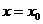является вертикальной асимптотой графика функции , если выполнено хотя бы одно из условий

.

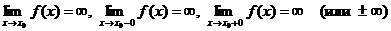Для разыскания вертикальных асимптот кривой поступаем следующим образом:

1) находим на оси 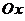точки разрыва функции ;

2) выделяем те из них, в которых хотя бы один из пределов функции (слева или справа) равен . Пусть это будут точки 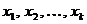. Тогда прямые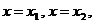 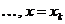будут вертикальными асимптотами графика функции .

Наклонные асимптоты

Теорема 4. Для того чтобы график функции имел 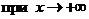наклонную асимптоту 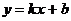, необходимо и достаточно, чтобы существовали оба предела

.

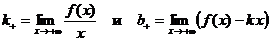Аналогично для случая .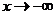

Горизонтальная асимптота (частный случай наклонной асимптоты )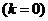

Если 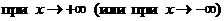функция имеет конечный предел, равный числу 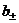: 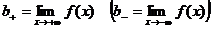, то прямая 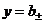есть горизонтальная асимптота соответственно для правой или левой ветви графика функции .

Правило отыскания асимптот очевидно из следующего образца.

Пример 10. Найти асимптоты кривой .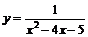

1. ▲ Найдем область определения функции: .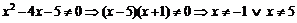

.

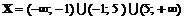Функция не определена в точках 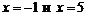. Определим тип разрыва в этих точках, для чего вычислим пределы ,

,

,

.

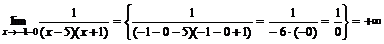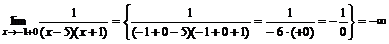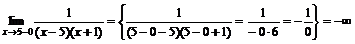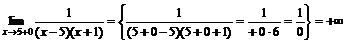Следовательно, прямые 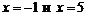вертикальные асимптоты.

2. Найдем левую наклонную асимптоту:

;

.

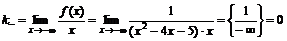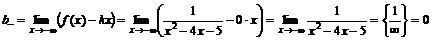Следовательно, имеем слева горизонтальную асимптоту .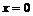

Найдем правую наклонную асимптоту:

;

.

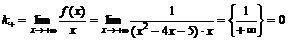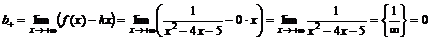Значит, справа имеем горизонтальную асимптоту .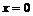

▼

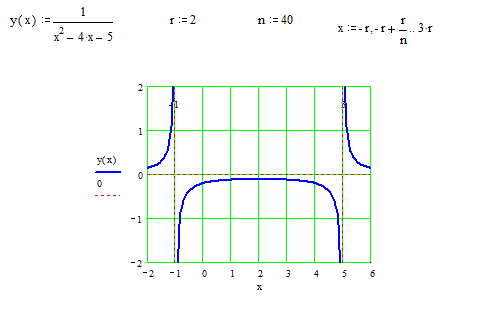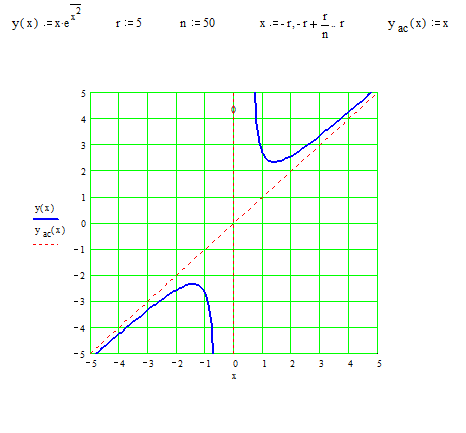
Пример 11. Найти асимптоты кривой .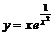

1. ▲ Найдем область определения функции: 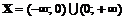. Функция не определена в точке 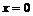. Определим тип разрыва в этой точке, для чего вычислим пределы

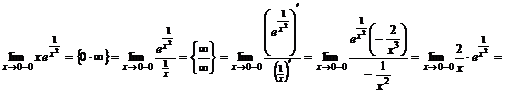
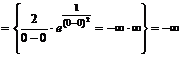
Аналогично получаем .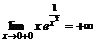

Прямая 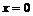– вертикальная асимптота.

2. Для нахождения левой наклонной асимптоты вычислим

,

.

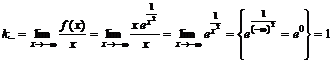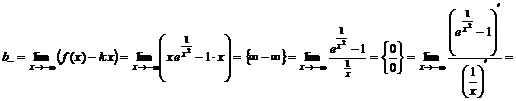
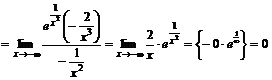Следовательно, прямая 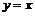– левая наклонная асимптота.

Аналогично для правой наклонной асимптоты получаем

.

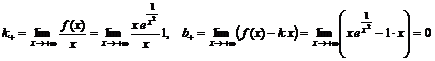Следовательно, прямая 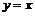– наклонная асимптота.

▼

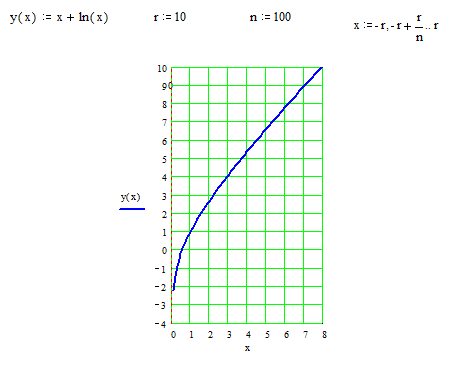
Пример 12. Найти асимптоты кривой .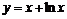

1. ▲ Найдем область определения функции: 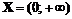. Поэтому вертикальная асимптота может существовать лишь на конечной границе области определения. Найдем

.

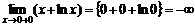Значит, прямая 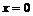– вертикальная асимптота.

2. Найдем правую наклонную асимптоту (так как ):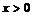

.

.

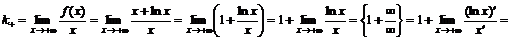
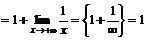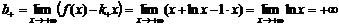Следовательно, наклонной асимптоты нет.

▼