Применение дифференциального исчисления
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
К ИССЛЕДОВАНИЮ ПОВЕДЕНИЯ ФУНКЦИЙ
 |

 |
Р Г Г М У
Санкт-Петербург
Одобрено Научно-методическим советом РГГМУ
УДК 51
Веретенников В. Н. Учебно-методическое пособие для выполнения индивидуального задания. Применение дифференциального исчисления к исследованию поведения функций. – СПб.: Изд. РГГМУ. 2007. – 36 с.
Активизация познавательной деятельности студентов, выработка у них способности самостоятельно решать достаточно сложные проблемы может быть достигнута при такой организации учебного процесса, когда каждому студенту выдаются индивидуальные домашние задания (ИДЗ) с обязательным последующим контролем их выполнения и выставлением оценок.
Предлагаемое пособие адресовано преподавателям и студентам и предназначено для проведения практических занятий и самостоятельных (контрольных) работ в аудитории и выдачи ИДЗ.
© Веретенников В. Н.
© Российский государственный гидрометеорологический университет (РГГМУ), 2007.
ПРЕДИСЛОВИЕ
"Математика" является не только мощным средством решения прикладных гидрометеорологических задач, но также и элементом общей культуры. Именно в рамках математического образования студент получает навыки творческого подхода к решению интеллектуальных проблем, точному пониманию средств возможностей решения проблем, знакомится с современными информационными технологиями.
Целью математического образования является:
1. Воспитание достаточно высокой математической культуры.
2. Привитие навыков современных видов математического мышления.
3. Привитие навыков использования математических методов и основ математического моделирования в практической деятельности.
Воспитание у студентов математической культуры включает в себя ясное понимание необходимости математической составляющей в общей подготовке студента. Он должен выработать представление о роли и месте математики в современной цивилизации и в мировой культуре, уметь логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений.
В пособии приведены основные теоретические сведения, отражающие базисные понятия по разделу "Применение дифференциального исчисления к исследованию поведения функций"; базисные методы решения основных задач; приведен перечень знаний, умений и навыков, которыми должен владеть студент; указана используемая литература.
ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Основные теоретические сведения
ЭКСТРЕМУМЫ ФУНКЦИИ
Рассмотрим функцию  , определенную в некоторой окрестности точки
, определенную в некоторой окрестности точки  , включая и саму точку
, включая и саму точку  .
.
Определение 3. Точка  называется точкой локального максимума, а значение функции в ней – локальным максимумом функции
называется точкой локального максимума, а значение функции в ней – локальным максимумом функции  , если существует такое
, если существует такое 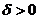 , что для всех
, что для всех 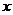 , удовлетворяющих условию
, удовлетворяющих условию 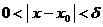 , верно неравенство
, верно неравенство 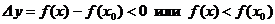 .
.
Определение 4. Точка  называется точкой локального минимума, а значение функции в ней – локальным минимумом функции
называется точкой локального минимума, а значение функции в ней – локальным минимумом функции  , если существует такое
, если существует такое 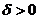 , что для всех
, что для всех 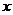 , удовлетворяющих условию
, удовлетворяющих условию 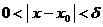 , верно неравенство
, верно неравенство 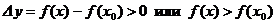 .
.
Точки локального максимума и минимума называются точками локального экстремума, а значения в них – локальными экстремумами функции.
Необходимое условие существования точек экстремума функции.
Теорема 2.1. Для того чтобы точка  была точкой экстремума функции
была точкой экстремума функции  , определенной в окрестности этой точки, необходимо выполнение одного из двух условий: либо
, определенной в окрестности этой точки, необходимо выполнение одного из двух условий: либо 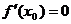 ; либо производная
; либо производная 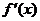 не существует в точке
не существует в точке  (в частности, где
(в частности, где 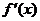 – бесконечно большая функция).
– бесконечно большая функция).
Такие точки называются критическими, и они являются точками, подозрительными на экстремум.
Достаточные условия экстремума.
I. Теорема 2.2. Пусть функция  , определенная в окрестности точки
, определенная в окрестности точки  , непрерывная в самой этой точке и дифференцируемая в некоторой
, непрерывная в самой этой точке и дифференцируемая в некоторой 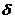 – окрестности точки
– окрестности точки  . Тогда справедливы следующие заключения:
. Тогда справедливы следующие заключения:
1) если 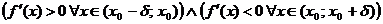 (т. е. при переходе
(т. е. при переходе 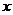 через критическую точку
через критическую точку  производная меняет знак с плюса на минус), то
производная меняет знак с плюса на минус), то  – точка локального максимума функции
– точка локального максимума функции  ;
;
2) если 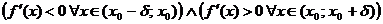 (т. е. при переходе
(т. е. при переходе 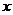 через критическую точку
через критическую точку  производная меняет знак с минуса на плюс), то
производная меняет знак с минуса на плюс), то  – точка локального минимума функции
– точка локального минимума функции  ;
;
3) если 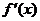 во всей
во всей 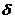 – окрестности точки
– окрестности точки  имеет один и тот же знак, то в точке
имеет один и тот же знак, то в точке  экстремума функции
экстремума функции  .
.
II. Теорема 2.3. Пусть функция  , определенная в окрестности точки
, определенная в окрестности точки  , имеет производные до 2-го порядка включительно. Если
, имеет производные до 2-го порядка включительно. Если 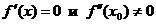 , то функция
, то функция  имеет в точке
имеет в точке  экстремум, а именно:
экстремум, а именно:
1) минимум, если 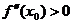 ,
,
2) максимум, если 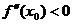 .
.
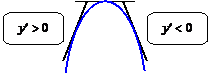
 Геометрический смысл необходимых и достаточных условий экстремумов
Геометрический смысл необходимых и достаточных условий экстремумов
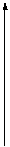 |  | ||||
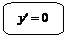 | |||||
y y
 | |||
 |

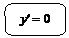

 O x O x
O x O x
Проследите за изменением производной в зоне 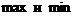 :
:
I. Слева функция возрастает, т. е. 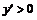 . В точке . В точке 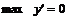 . Справа функция убывает, т. е. . Справа функция убывает, т. е. 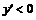 . . | I. Слева функция убывает, т. е. 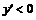 . В точке . В точке 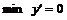 . Справа функция возрастает, т. е. . Справа функция возрастает, т. е. 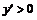 . . | |
II. 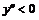 | II.  |
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
Может оказаться, что размеры графика данной функции 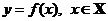 , не ограничены. Это бывает, когда функция не ограничена или когда она задана на неограниченном промежутке. В таких случаях часто представление о графике функции вне рамок чертежа дают асимптоты графика.
, не ограничены. Это бывает, когда функция не ограничена или когда она задана на неограниченном промежутке. В таких случаях часто представление о графике функции вне рамок чертежа дают асимптоты графика.
Определение. Прямая 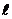 называется асимптотой кривой
называется асимптотой кривой  , если расстояние
, если расстояние 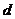 от точки
от точки 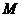 кривой
кривой  до прямой
до прямой 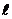 стремится к нулю при неограниченном удалении точки
стремится к нулю при неограниченном удалении точки 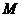 по какой-либо части кривой
по какой-либо части кривой  от начала координат.
от начала координат.
Различают три вида асимптот: вертикальные (параллельные оси 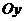 ), горизонтальные (параллельные оси
), горизонтальные (параллельные оси 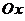 ) и наклонные (не параллельные ни одной из координатных осей).
) и наклонные (не параллельные ни одной из координатных осей).
Прямая 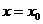 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  , если выполнено хотя бы одно из условий
, если выполнено хотя бы одно из условий
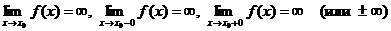 .
.
Для разыскания вертикальных асимптот кривой  поступаем следующим образом:
поступаем следующим образом:
1) находим на оси 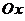 точки разрыва функции
точки разрыва функции  ;
;
2) выделяем те из них, в которых хотя бы один из пределов функции  (слева или справа) равен
(слева или справа) равен  . Пусть это будут точки
. Пусть это будут точки 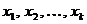 . Тогда прямые
. Тогда прямые 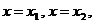
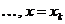 будут вертикальными асимптотами графика функции
будут вертикальными асимптотами графика функции  .
.
Наклонные асимптоты
Теорема 4. Для того чтобы график функции  имел
имел 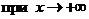 наклонную асимптоту
наклонную асимптоту 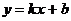 , необходимо и достаточно, чтобы существовали оба предела
, необходимо и достаточно, чтобы существовали оба предела
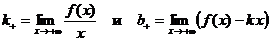 .
.
Аналогично для случая 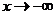 .
.
Горизонтальная асимптота (частный случай наклонной асимптоты 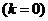 )
)
Если 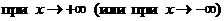 функция
функция  имеет конечный предел, равный числу
имеет конечный предел, равный числу 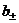 :
: 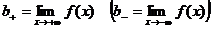 , то прямая
, то прямая 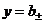 есть горизонтальная асимптота соответственно для правой или левой ветви графика функции
есть горизонтальная асимптота соответственно для правой или левой ветви графика функции  .
.
Правило отыскания асимптот очевидно из следующего образца.
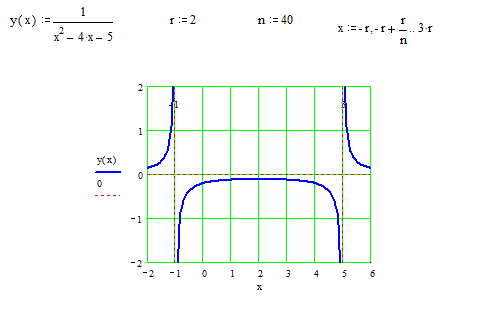
Пример 10. Найти асимптоты кривой 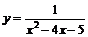 .
.
1. ▲ Найдем область определения функции: 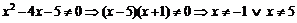 .
.
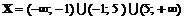 .
.
Функция не определена в точках 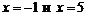 . Определим тип разрыва в этих точках, для чего вычислим пределы
. Определим тип разрыва в этих точках, для чего вычислим пределы 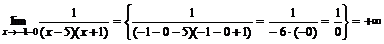 ,
,
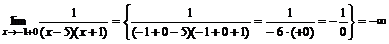 ,
,
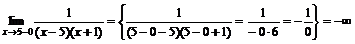 ,
,
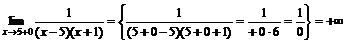 .
.
Следовательно, прямые 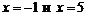 вертикальные асимптоты.
вертикальные асимптоты.
2. Найдем левую наклонную асимптоту:
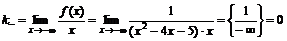 ;
;
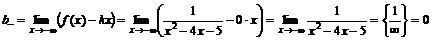 .
.
Следовательно, имеем слева горизонтальную асимптоту 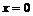 .
.
Найдем правую наклонную асимптоту:
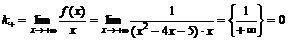 ;
;
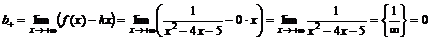 .
.
Значит, справа имеем горизонтальную асимптоту 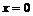 .
.
 ▼
▼
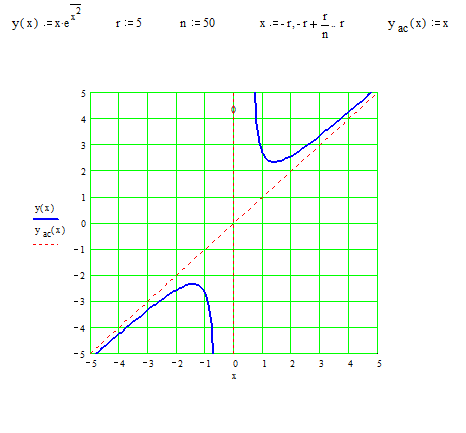
Пример 11. Найти асимптоты кривой 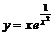 .
.
1. ▲ Найдем область определения функции: 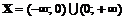 . Функция не определена в точке
. Функция не определена в точке 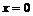 . Определим тип разрыва в этой точке, для чего вычислим пределы
. Определим тип разрыва в этой точке, для чего вычислим пределы
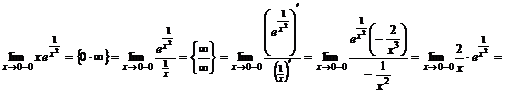
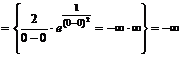
Аналогично получаем 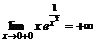 .
.
Прямая 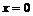 – вертикальная асимптота.
– вертикальная асимптота.
2. Для нахождения левой наклонной асимптоты вычислим
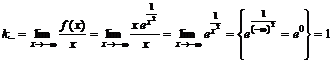 ,
,
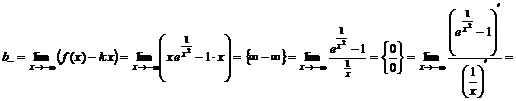
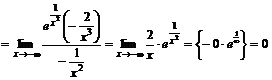 .
.
Следовательно, прямая 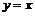 – левая наклонная асимптота.
– левая наклонная асимптота.
Аналогично для правой наклонной асимптоты получаем
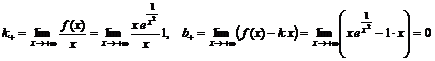 .
.
Следовательно, прямая 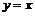 – наклонная асимптота.
– наклонная асимптота.
 ▼
▼
Пример 12. Найти асимптоты кривой 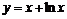 .
.
1. ▲ Найдем область определения функции: 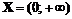 . Поэтому вертикальная асимптота может существовать лишь на конечной границе области определения. Найдем
. Поэтому вертикальная асимптота может существовать лишь на конечной границе области определения. Найдем
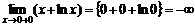 .
.
Значит, прямая 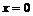 – вертикальная асимптота.
– вертикальная асимптота.
2. Найдем правую наклонную асимптоту (так как 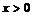 ):
):
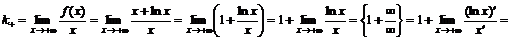
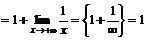 .
.
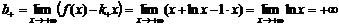 .
.
Следовательно, наклонной асимптоты нет.
 ▼
▼
Элементарное исследование
1. Найти область определения функции.
2. Найти точки разрыва функции. Их характер. Вертикальные асимптоты.
3. Исследовать функцию на симметричность (определить четность и нечетность функции) и периодичность.
4. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с осями координат. Найти интервалы знакопостоянства.
5. Вычислить предельные значения функции в ее граничных точках.
6. Выяснить существование наклонных асимптот.
Промежутки знакопостоянства
 | 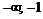 | –1 | 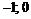 | 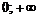 | |
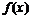 | + | 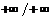 | + | – |
II. Исследование графика функции по первой производной.
Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
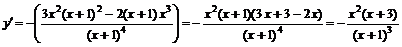 .
.
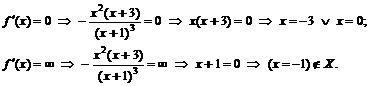
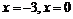 к. т. I.
к. т. I.
Область определения функции разобьем на интервалы 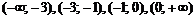 и определим знак
и определим знак 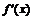 в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом
в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом 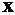 ) с указанием поведения функции на этих интервалах занесем в таблицу:
) с указанием поведения функции на этих интервалах занесем в таблицу:
 | 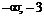 | –3 | 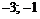 | –1 | 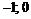 | 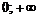 | |
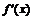 | – | + | 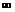 | – | – | ||
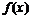 | 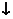 | 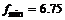 | 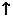 |  |  |  |
Так как функция в точке 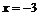 определена и непрерывна и при переходе через нее
определена и непрерывна и при переходе через нее 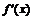 меняет знак с минуса на плюс, то в этой точке минимум, причем
меняет знак с минуса на плюс, то в этой точке минимум, причем 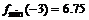 .
.
III. Исследование графика функции по второй производной.
Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
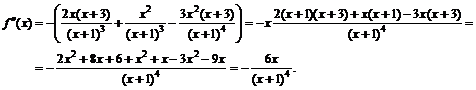
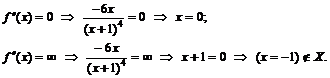
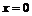 к. т. II.
к. т. II.
Область определения функции разобьем на интервалы 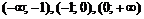 и определим знак
и определим знак  в каждом из них. Результат исследования знака функции
в каждом из них. Результат исследования знака функции  на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:
на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:
 | 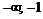 | –1 | 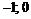 | 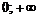 | |
 | + | 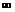 | + | – | |
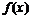 | 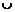 | 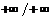 |  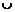 | 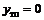 | 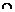 |
При переходе через точку 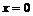 вторая производная меняет знак, следовательно, это точка перегиба функции, причем
вторая производная меняет знак, следовательно, это точка перегиба функции, причем 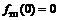 . Точка
. Точка 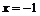 не является точкой перегиба.
не является точкой перегиба.
Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.
В окончательном виде график изображен на следующем рисунке.
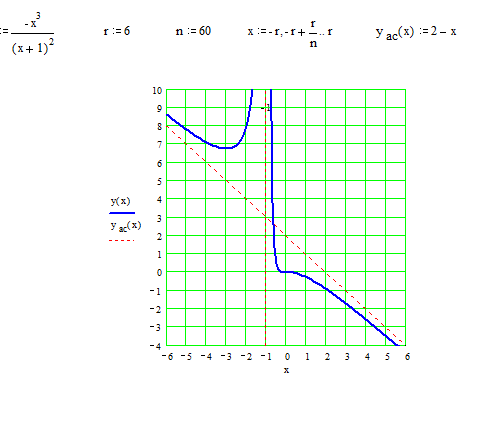 ▼
▼
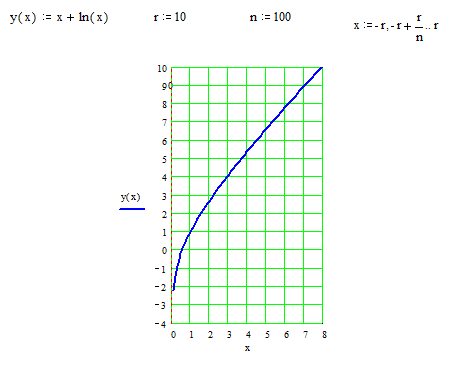
Пример 14. Провести полное исследование функции 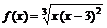 и построить ее график.
и построить ее график.
▲Исследование функции будем проводить, придерживаясь приведенной выше схемы.
I. Элементарное исследование
· Область определения функции. 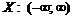 .
.
· Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
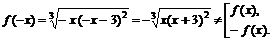 Функция общего вида.
Функция общего вида.
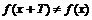 . Функция не периодична.
. Функция не периодична.
· Выясним существование асимптот.
Вертикальных асимптот нет, так как нет точек разрыва.
Найдем наклонные асимптоты 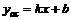 .
.
Слева 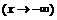 .
.
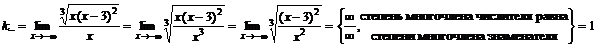 ,
,
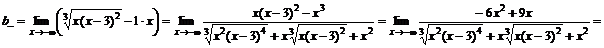
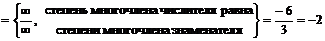 .
.
Уравнение наклонной асимптоты слева 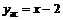 .
.
Справа 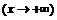 .
.
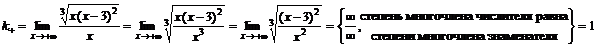 ,
,
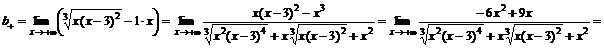
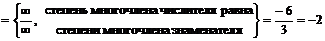 .
.
Уравнение наклонной асимптоты справа 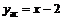 .
.
· Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.
Точки пересечения с осью 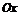 :
: 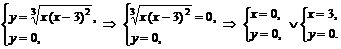
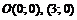 .
.
Точки пересечения с осью 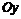 :
: 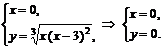
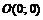 .
.
Промежутки знакопостоянства
 | 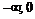 | 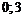 | 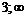 | ||
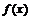 | – | + | + |
II. Исследование графика функции по первой производной.
Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
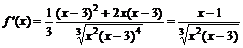 .
.
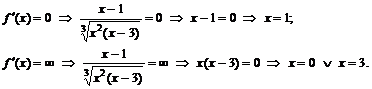
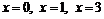 к. т. I.
к. т. I.
Область определения функции разобьем на интервалы 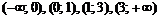 и определим знак
и определим знак 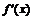 в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом
в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом 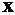 ) с указанием поведения функции на этих интервалах занесем в таблицу:
) с указанием поведения функции на этих интервалах занесем в таблицу:
 | 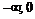 | 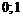 | 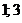 | 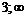 | |||
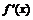 | + |  | + | – |  | + | |
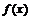 |  | 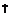 | 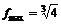 | 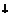 | 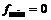 | 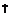 |
Так как функция в точке 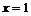 определена и непрерывна и при переходе через нее
определена и непрерывна и при переходе через нее 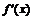 меняет знак с плюса на минус, то в этой точке максимум, причем
меняет знак с плюса на минус, то в этой точке максимум, причем 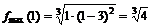 . В точке
. В точке 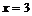 функция определена и непрерывна и при переходе через нее
функция определена и непрерывна и при переходе через нее 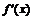 меняет знак с минуса на плюс, следовательно, в этой точке минимум, причем
меняет знак с минуса на плюс, следовательно, в этой точке минимум, причем 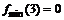 .
.
III. Исследование графика функции по второй производной.
Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
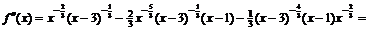
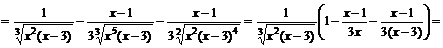
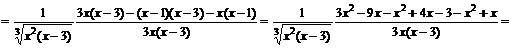
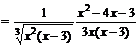 .
.
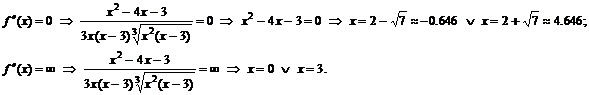
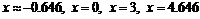 к. т. II.
к. т. II.
Область определения функции разобьем на интервалы 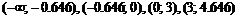 ,
, 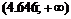 и определим знак
и определим знак  в каждом из них. Результат исследования знака функции
в каждом из них. Результат исследования знака функции  на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:
на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:
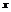 | 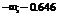 | –0.646 | 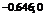 | 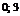 | 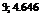 | 4.646 | 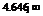 | ||
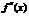 | – | + | 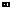 | – | 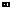 | – | + | ||
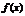 | 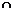 | 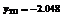 | 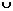 | 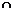 | 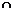 | 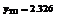 | 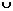 |
При переходе через точки  вторая производная меняет знак, следовательно, это точки перегиба функции, причем
вторая производная меняет знак, следовательно, это точки перегиба функции, причем
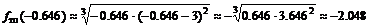 ,
,
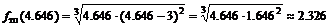 .
.
Точки перегиба: 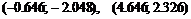 .
.
Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.
В окончательном виде график изображен на следующем рисунке.
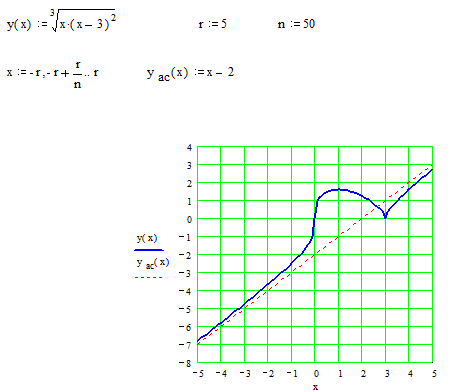 ▼
▼
Пример 15. Провести полное исследование функции 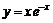 и построить ее график.
и построить ее график.
▲Исследование функции будем проводить, придерживаясь приведенной выше схемы.
I. Элементарное исследование
· Область определения функции. 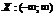 .
.
· Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
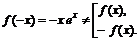 Функция общего вида.
Функция общего вида.
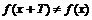 . Функция не периодична.
. Функция не периодична.
· Выясним существование асимптот.
Вертикальных асимптот нет, так как нет точек разрыва.
Найдем наклонные асимптоты 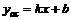 .
.
Слева 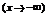 .
.
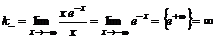 . Слева наклонной асимптоты нет.
. Слева наклонной асимптоты нет.
Справа 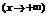 .
.
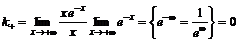 ,
,
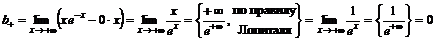 .
.
Справа горизонтальная асимптота: 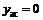 .
.
· Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.
Точки пересечения с осью 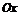 :
: 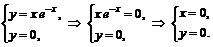
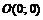 .
.
Точки пересечения с осью 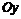 :
: 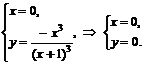
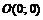 .
.
Промежутки знакопостоянства
 | 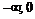 | 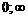 | |
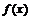 | – | + |
II. Исследование графика функции по первой производной.
Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
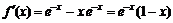 .
.
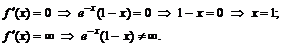
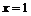 к. т. I.
к. т. I.
Область определения функции разобьем на интервалы 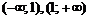 и определим знак
и определим знак 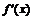 в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом
в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом 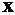 ) с указанием поведения функции на этих интервалах занесем в таблицу:
) с указанием поведения функции на этих интервалах занесем в таблицу:
 | 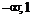 | 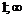 | |
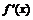 | + | – | |
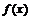 | 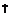 | 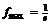 | 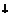 |
Так как функция в точке 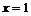 определена и непрерывна и при переходе через нее
определена и непрерывна и при переходе через нее 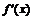 меняет знак с плюса на минус, то в этой точке максимум, причем
меняет знак с плюса на минус, то в этой точке максимум, причем 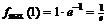 .
.
III. Исследование графика функции по второй производной.
Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
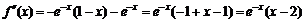 .
.
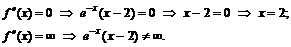
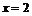 к. т. II.
к. т. II.
Область определения функции разобьем на интервалы 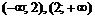 и определим знак
и определим знак  в каждом из них. Результат исследования знака функции
в каждом из них. Результат исследования знака функции  на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:
на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:
 | 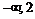 | 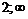 | |
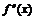 | – | + | |
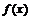 | 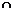 | 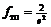 | 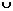 |
При переходе через точку 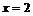 вторая производная меняет знак, следовательно, это точка перегиба функции, причем
вторая производная меняет знак, следовательно, это точка перегиба функции, причем 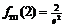 . Точка перегиба:
. Точка перегиба: 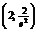 .
.
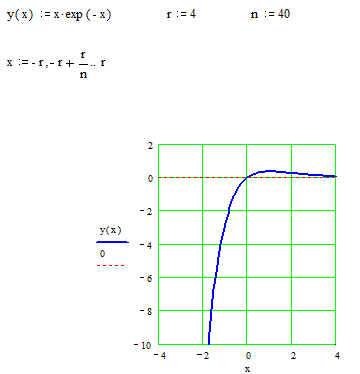
Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.
В окончательном виде график изображен на следующем рисунке.
 ▼
▼
Пример 16. Провести полное исследование функции 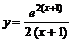 и построить ее график.
и построить ее график.
▲Исследование функции будем проводить, придерживаясь приведенной выше схемы.
I. Элементарное исследование
· Область определения функции 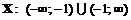 . Точка разрыва:
. Точка разрыва: 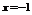 .
.
· Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
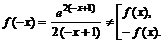 Функция общего вида.
Функция общего вида.
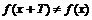 . Функция не периодична.
. Функция не периодична.
· Выясним существование асимптот. В точке 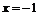 функция имеет разрыв II рода, ибо,
функция имеет разрыв II рода, ибо,
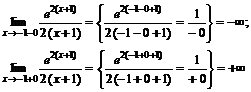
в остальных точках она непрерывна. Прямая 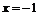 является вертикальной асимптотой.
является вертикальной асимптотой.
Найдем наклонные асимптоты 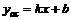 .
.
Слева 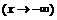 .
.
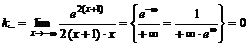 ,
,
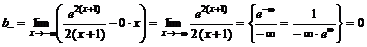 .
.
Уравнение горизонтальной асимптоты слева: 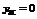 .
.
Справа 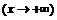 .
.
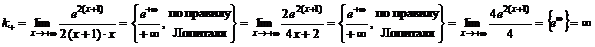 .
.
Справа наклонной асимптоты нет.
· Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.
Точки пересечения с осью 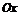 :
: 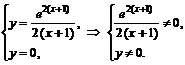 Точек пересечения с осью
Точек пересечения с осью 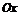 нет.
нет.
Точки пересечения с осью 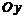 :
: 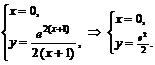 Точка пересечения с осью
Точка пересечения с осью 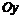 :
: 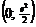 .
.
Промежутки знакопостоянства
 | 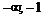 | –1 | 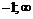 |
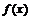 | – | 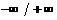 | + |
II. Исследование графика функции по первой производной.
Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
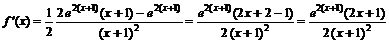 .
.
