Выпуклость и вогнутость графика функции. Точки перегиба.

СОДЕРЖАНИЕ

1.Б.М.В по определению Стр1.

2.Б.Б.В по определению Стр1.

3.Асимптоты Стр2.

4.Выпуклость и вогнутость графика функции.

Точки перегиба. Стр3.

5.Монотонность функции (экстремум) Стр4.

6.Исследование графика функции Стр5.

7.Раскрытие неопределенностей,

(таблица эквивалентности) Стр6.

8.Сравнение бесконечно малых Стр7.

9.Непрерывность, разрывность функции Стр8.

10.Дифференцируемость функции Стр9.

11.Порядок малости Стр10.

12.Частные производные первого порядка ФНП Стр10.

13.Частные производные высшего порядка ФНП Стр10.

14.Дифференциалы 1 и 2 порядка: Стр10.

15.Касательная и нормаль Стр11.

16.Экстремум фнп Стр11.

17.Производная по направлению Стр12.

18.Градиент Стр12.

19.Нахождение дифференциала Стр12.

20.Формула Тейлора (Остаточный член Пеано стр14) Стр13.

21.Частная производная третьего порядка ФНП Стр13.

22.Эквивалентность Б.М и Б.Б. Стр14.

23.Производные первого порядка для неявно заданной функции

24.Непрерывность и диф-сть ФНП Стр14.

25.Вычисление приближённо Стр15.

26.Производные высших порядков заданных параметрически Стр15

27.Экстремумы трех переменных Стр16.

Варианты определения.

Говорят, 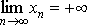что , если .

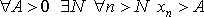Говорят, 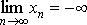что , если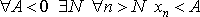

Последовательность {x_n} называется БЕСКОНЕЧНО БОЛЬШОЙ, если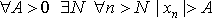

(то есть, если )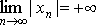

Последовательность {x_n} называется БЕСКОНЕЧНО МАЛОЙ, если 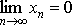, то есть если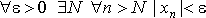

АСИМПТОТЫ

Прямая x = a называется ВЕРТИКАЛЬНОЙ АСИМПТОТОЙ графика функции f (x) при x → a, если выполнено хотя бы одно из условий :

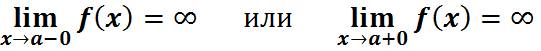
(нужно найти Lim с права и с лево, заданной функции, если придел окажется равен бесконечности, то значит существуют вертикальные асимптоты, а если 0 то не сущ.)

Прямая y=kx+b, k ≠ 0 называется НАКЛОННОЙ АСИМПТОТОЙ графика функции f (x) при x → +∞, если

Чтобы найти наклонную асимптоту функции f(x) при x → ±∞, нужно сначала найти два предела:

Когда k и b найдены, строим прямую kx+b. Она и будет наклонной асимптотой.

Если один из вышеназванных пределов не существует или они бесконечны, то наклонной асимптоты у функции просто нет.

ГОРИЗОНТАЛЬНАЯ АСИМПТОТА — прямая вида y = b при условии существования предела

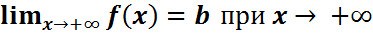
МОНОТОННОСТЬ ФУНКЦИЙ

Точки, в которых достигается максимум или минимум и точки разрыва функции, называются точками экстремума.

АЛГОРИТМ НАХОЖДЕНИЯ ЭКСТРЕМУМОВ:

1. Находим производную функции

2. Приравниваем эту производную к нулю

3. Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль)

4. Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум

5. Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную.

6. Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом.

7. Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.

Если для любого 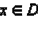(x ≠ a) выполняется неравенство f (x) ≤ f (a) 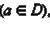то точка a называется точкой наибольшего значения функции на множестве D:

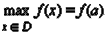
Если для любого 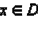(x ≠ b) выполняется неравенство f (x) > f (b) 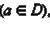то точка b называется точкой наименьшего значения функции на множестве D.

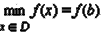
Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.

Исследование графика функции:

1.Область определения D(f)

2.т. Чётные или нечетные

3.Lim f(x) при х-> +(-) &

4.Асимптоты

5.f '

6.f ’’

7.График

РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ:

Раскрытие неопределенностей вида 0⋅ ∞ .Неопределенности вида 0⋅ ∞ сводятся к неопределенностям вида ∞*∞ .

Раскрытие неопределенностей вида1^∞ .Применяется второй замечательный предел.

1)

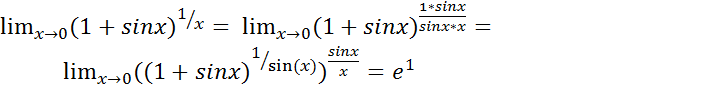
2) =

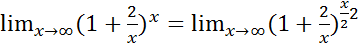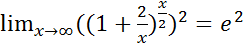
Число e, второй замечательный предел. Числом e называется предел

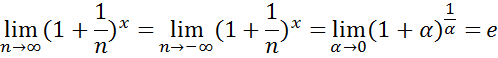
Раскрытие неопределенностей вида 0⁰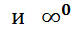

Логарифмируем выражение и используем равенство:

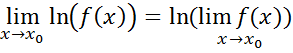
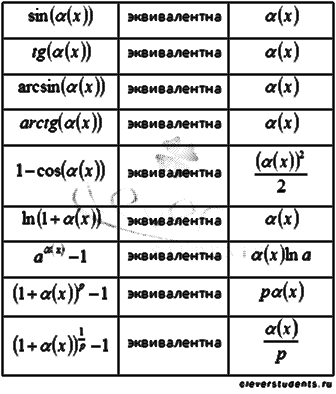
ТАБЛИЦА ЭКВИВАЛЕНТНОСТИ

СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ

Отношение бесконечно малых величин образует так называемую неопределённость (0/0).

Чтобы сравнить две бесконечно малые величины нужно найти предел их отношений:

1. Если 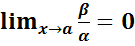, то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).

2. Если 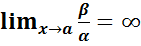, то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).

3. Если 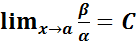, (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.

Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения). В частности если С=1 то α(х) и β(х) называются эквивалентными.

4. Если 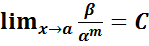(предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

Для вычисления подобных пределов удобно использовать правило Лопиталя.

НЕПРЕРЫВНОСТЬ ФУНКЦИИ

Функция f(x) называется непрерывной в точке х₀, если

1. Она определена в точке х₀

2. Существуют конечные пределы:

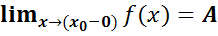
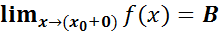
3. Эти пределы равны между собой и равны значению функции в точке х₀

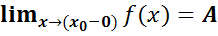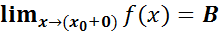) = ( ) =f(x₀)

РАЗРЫВНОСТЬ ФУНКЦИИ

Итак, если хотя бы одно из трех условий непрерывности не выполняется, функция называется разрывной в точке х₀, а сама точка x₀-точкой разрыва.

1. Если в точке x₀ оба односторонних разных предела существуют и конечны, то разрыв называется разрывом первого рода. Пусть х₀-точка разрыва первого рода, т.е.

Возможны два случая:

1. f(x₀+0)=f(x₀-0)=L, но либо функция f(x) не определена в точке х₀, (то есть не выполнено либо первое либо третье условие непрерывности). В этом случае разрыв называется устранимым, так как если доопределить функцию в точке х₀ или переопределить ее, положив f(x₀)=L, функция f(x) станет непрерывной в точке х₀.

2. f(x₀-0) ≠ f(x₀+0) B этом случае разрыв называется неустранимым. Разность абсолютной величины односторонних пределов есть – скачок функции.

2. Если же хотя бы один из односторонних пределов f(x₀+0) или f(x₀-0) не существует или бесконечен, то разрыв называется разрывом второго рода. Разрыв второго рода всегда неустранимый. Если в точке х₀ функции f(x) и g(x) непрерывны, то в этой же точке непрерывными являются и функции

§6 ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ.

Функция 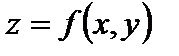называется дифференцируемой в точке 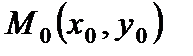, если в некоторой окрестности этой точки полное приращение этой функции можно представить в виде

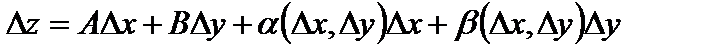, (1)

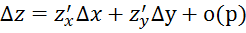
Z=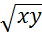

1) Находим первую производную:

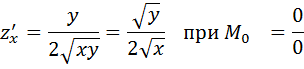
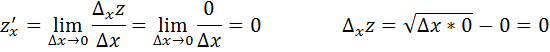
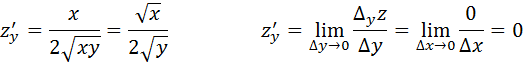
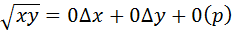
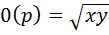
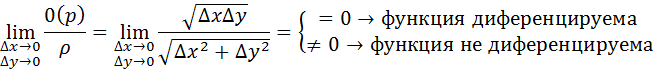
Доказательство. Переходя в соотношении (1) к пределу при 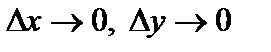получим 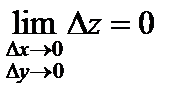, следовательно, функция непрерывна (согласно определению непрерывности функции двух переменных на языке приращений).
Теорема 2 (необходимое условие дифференцируемости).

Если функция 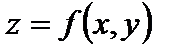дифференцируема в точке 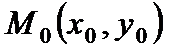, то в этой точке существуют частные производные, причём

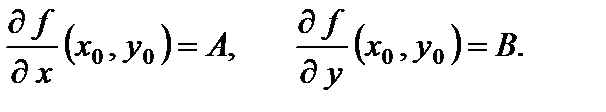
Доказательство. По условию теоремы функция 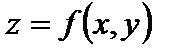дифференцируема, значит, имеет место соотношение (1). Полагая 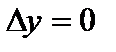, имеем, что 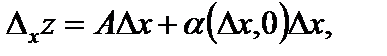где 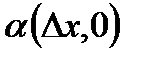─ бесконечно малая функция при .

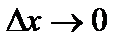Разделив на 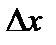и переходя к пределу при 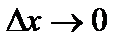, получаем

.

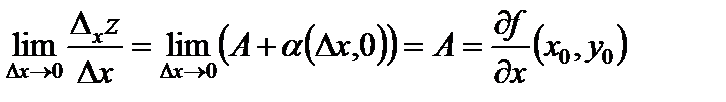ПОРЯДОК МАЛОСТИ:

Порядок малости находиться по таблице эквивалентности:

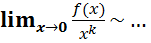незабываем ставить знак эквивалентности), k – есть порядок малости.

КАСАТЕЛЬНАЯ И НОРМАЛЬ

Касательная -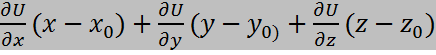

Нормаль -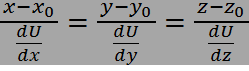

ЭКСТРЕМУМ ФНП

1) находим частные производные от функции

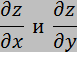
2) Составляем систему уравнения

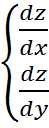Выделяем Х и У, х=… и у=…

Подставляем х и у в систему находим соответствующие точки (х₁;у₁) и (х₂;у₂) т.е. М₁(х₁;у₁) и М₂(х₂;у₂)

3) Вычислим вторую производную

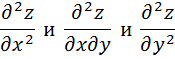
4) Рассматриваем точки М₁(х₁;у₁) и М₂(х₂;у₂) …..

Подставляя значения точек М_n(х_n;у_n) во II производную

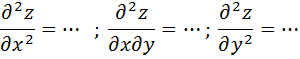
5) Составляем матрицу А со значениями второй производной:

s w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 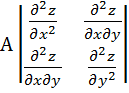затем находим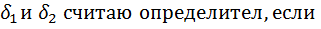

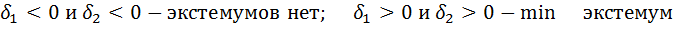
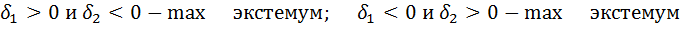
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ

Z=x³-3x³y+3xy²+1 и точки M(3;1) и М₁(6;5)

1) Находим l=(вектор)MM₁={3;4}

2) Находим длину |l|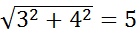

3) l₀={ 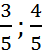} где, x=cosα, y=cosβ

4) Находим первые производные 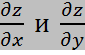и подставляем в место х и узначения точки M₀

5) И все найденное подставляем в формулу:

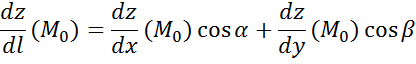
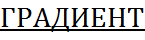
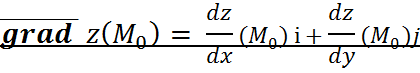
Нахождение ДИФФЕРЕНЦИАЛА.

1. Сначала находим производную

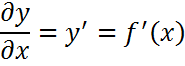
2. Затем придел производной

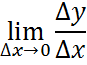
3. Потом и сам дифференциал

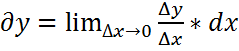
ФОРМУЛА ТЕЙЛОРА

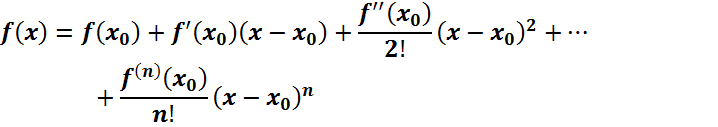
Эквивалентность Б.М и Б.Б.

Чтобы сравнить две бесконечно малые величины, нужно найти предел их отношений. И по таблице эквивалентности.

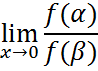
Производные первого порядка для неявно заданной функции:

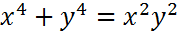
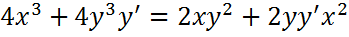
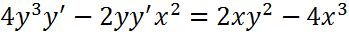
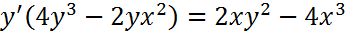
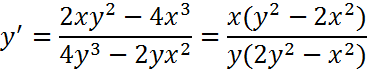
Остаточный член форма Пеано

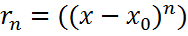где M( 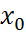). Для формулы Тейлора

Непрерывность и диф-сть ФНП

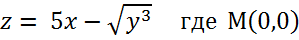
Непрерывность:

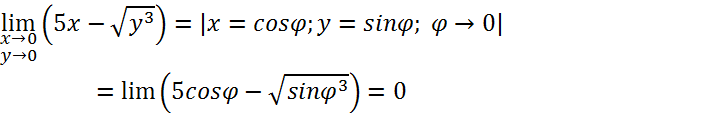
Диф-ть: (зададим приращение)

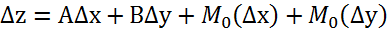
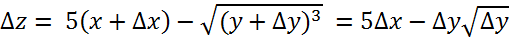
Вычисление приближённо

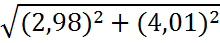
Вычислим приближённо с помощью дифференциала

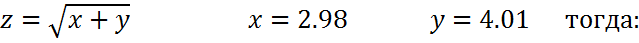
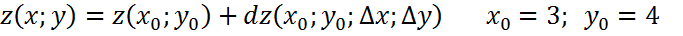
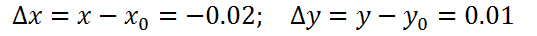
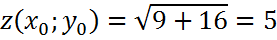
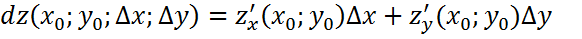
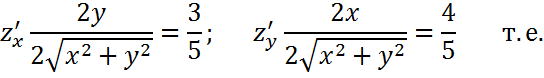
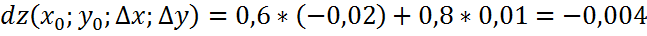
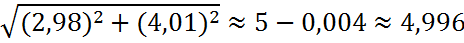
Экстремумы трех переменных

1. Находим первые производные

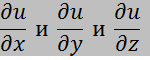
2. Составляем систему уравнения

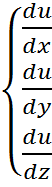Выделяем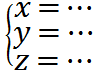

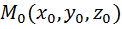
Подставляем х и у в систему находим соответствующие точки (х₁;у₁) и (х₂;у₂) т.е. М₁(х₁;у₁) и М₂(х₂;у₂)

3. Находим все вторые частные производные

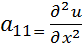
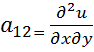
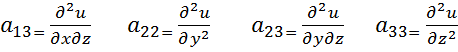
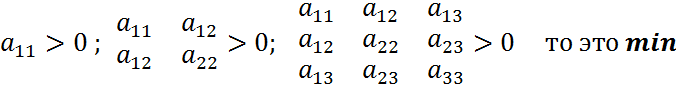
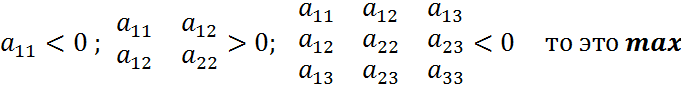
СОДЕРЖАНИЕ

1.Б.М.В по определению Стр1.

2.Б.Б.В по определению Стр1.

3.Асимптоты Стр2.

4.Выпуклость и вогнутость графика функции.

Точки перегиба. Стр3.

5.Монотонность функции (экстремум) Стр4.

6.Исследование графика функции Стр5.

7.Раскрытие неопределенностей,

(таблица эквивалентности) Стр6.

8.Сравнение бесконечно малых Стр7.

9.Непрерывность, разрывность функции Стр8.

10.Дифференцируемость функции Стр9.

11.Порядок малости Стр10.

12.Частные производные первого порядка ФНП Стр10.

13.Частные производные высшего порядка ФНП Стр10.

14.Дифференциалы 1 и 2 порядка: Стр10.

15.Касательная и нормаль Стр11.

16.Экстремум фнп Стр11.

17.Производная по направлению Стр12.

18.Градиент Стр12.

19.Нахождение дифференциала Стр12.

20.Формула Тейлора (Остаточный член Пеано стр14) Стр13.

21.Частная производная третьего порядка ФНП Стр13.

22.Эквивалентность Б.М и Б.Б. Стр14.

23.Производные первого порядка для неявно заданной функции

24.Непрерывность и диф-сть ФНП Стр14.

25.Вычисление приближённо Стр15.

26.Производные высших порядков заданных параметрически Стр15

27.Экстремумы трех переменных Стр16.

Варианты определения.

Говорят, 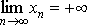что , если .

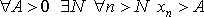Говорят, 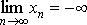что , если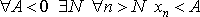

Последовательность {x_n} называется БЕСКОНЕЧНО БОЛЬШОЙ, если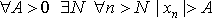

(то есть, если )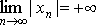

Последовательность {x_n} называется БЕСКОНЕЧНО МАЛОЙ, если 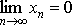, то есть если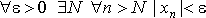

АСИМПТОТЫ

Прямая x = a называется ВЕРТИКАЛЬНОЙ АСИМПТОТОЙ графика функции f (x) при x → a, если выполнено хотя бы одно из условий :

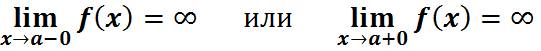
(нужно найти Lim с права и с лево, заданной функции, если придел окажется равен бесконечности, то значит существуют вертикальные асимптоты, а если 0 то не сущ.)

Прямая y=kx+b, k ≠ 0 называется НАКЛОННОЙ АСИМПТОТОЙ графика функции f (x) при x → +∞, если

Чтобы найти наклонную асимптоту функции f(x) при x → ±∞, нужно сначала найти два предела:

Когда k и b найдены, строим прямую kx+b. Она и будет наклонной асимптотой.

Если один из вышеназванных пределов не существует или они бесконечны, то наклонной асимптоты у функции просто нет.

ГОРИЗОНТАЛЬНАЯ АСИМПТОТА — прямая вида y = b при условии существования предела

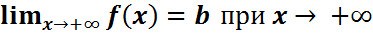
Выпуклость и вогнутость графика функции. Точки перегиба.

График функции y=f(x) называется ВЫПУКЛЫМ НА ИНТЕРВАЛЕ (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется ВОГНУТЫМ НА ИНТЕРВАЛЕ (a; b), если он расположен выше любой своей касательной на этом интервале.

Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.

Точка кривой, в которой кривая меняет направление изгиба, т.е. переходит от выпуклости вверх к выпуклости вниз или наоборот, называется точкой перегиба кривой. Для определения точек перегиба находят вторую производную.

В точке перегиба вторая производная равна нулю или не существует.

- если вторая производная положительна, то график функции выпуклый вниз.

- если вторая производная отрицательная, то график функции выпуклый вверх.

.

МОНОТОННОСТЬ ФУНКЦИЙ

Точки, в которых достигается максимум или минимум и точки разрыва функции, называются точками экстремума.

АЛГОРИТМ НАХОЖДЕНИЯ ЭКСТРЕМУМОВ:

1. Находим производную функции

2. Приравниваем эту производную к нулю

3. Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль)

4. Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум

5. Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную.

6. Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом.

7. Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.

Если для любого 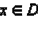(x ≠ a) выполняется неравенство f (x) ≤ f (a) 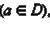то точка a называется точкой наибольшего значения функции на множестве D:

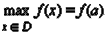
Если для любого 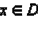(x ≠ b) выполняется неравенство f (x) > f (b) 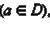то точка b называется точкой наименьшего значения функции на множестве D.

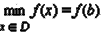
Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.

Исследование графика функции:

1.Область определения D(f)

2.т. Чётные или нечетные

3.Lim f(x) при х-> +(-) &

4.Асимптоты

5.f '

6.f ’’

7.График

РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ:

Раскрытие неопределенностей вида 0⋅ ∞ .Неопределенности вида 0⋅ ∞ сводятся к неопределенностям вида ∞*∞ .

Раскрытие неопределенностей вида1^∞ .Применяется второй замечательный предел.

1)

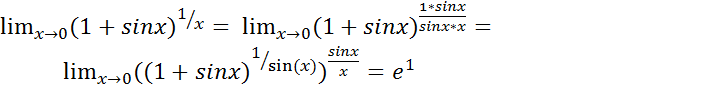
2) =

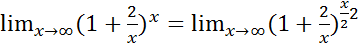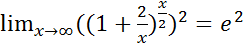
Число e, второй замечательный предел. Числом e называется предел

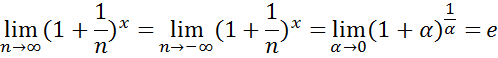
Раскрытие неопределенностей вида 0⁰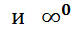

Логарифмируем выражение и используем равенство:

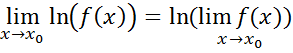
ТАБЛИЦА ЭКВИВАЛЕНТНОСТИ

СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ

Отношение бесконечно малых величин образует так называемую неопределённость (0/0).

Чтобы сравнить две бесконечно малые величины нужно найти предел их отношений:

1. Если 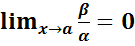, то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).

2. Если 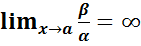, то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).

3. Если 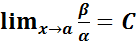, (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.

Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения). В частности если С=1 то α(х) и β(х) называются эквивалентными.

4. Если 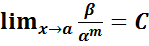(предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

Для вычисления подобных пределов удобно использовать правило Лопиталя.

НЕПРЕРЫВНОСТЬ ФУНКЦИИ

Функция f(x) называется непрерывной в точке х₀, если

1. Она определена в точке х₀

2. Существуют конечные пределы:

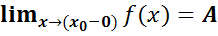
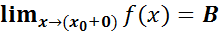
3. Эти пределы равны между собой и равны значению функции в точке х₀

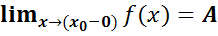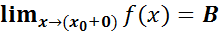) = ( ) =f(x₀)

РАЗРЫВНОСТЬ ФУНКЦИИ

Итак, если хотя бы одно из трех условий непрерывности не выполняется, функция называется разрывной в точке х₀, а сама точка x₀-точкой разрыва.

1. Если в точке x₀ оба односторонних разных предела существуют и конечны, то разрыв называется разрывом первого рода. Пусть х₀-точка разрыва первого рода, т.е.

Возможны два случая:

1. f(x₀+0)=f(x₀-0)=L, но либо функция f(x) не определена в точке х₀, (то есть не выполнено либо первое либо третье условие непрерывности). В этом случае разрыв называется устранимым, так как если доопределить функцию в точке х₀ или переопределить ее, положив f(x₀)=L, функция f(x) станет непрерывной в точке х₀.

2. f(x₀-0) ≠ f(x₀+0) B этом случае разрыв называется неустранимым. Разность абсолютной величины односторонних пределов есть – скачок функции.

2. Если же хотя бы один из односторонних пределов f(x₀+0) или f(x₀-0) не существует или бесконечен, то разрыв называется разрывом второго рода. Разрыв второго рода всегда неустранимый. Если в точке х₀ функции f(x) и g(x) непрерывны, то в этой же точке непрерывными являются и функции

§6 ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ.

Функция 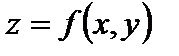называется дифференцируемой в точке 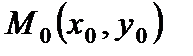, если в некоторой окрестности этой точки полное приращение этой функции можно представить в виде

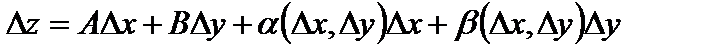, (1)

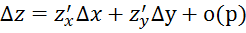
Z=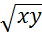

1) Находим первую производную:

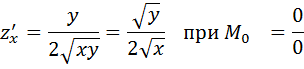
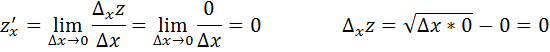
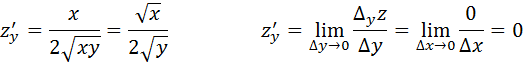
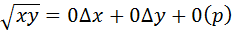
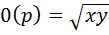
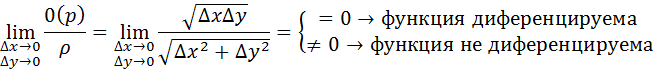
Доказательство. Переходя в соотношении (1) к пределу при 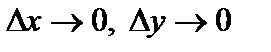получим 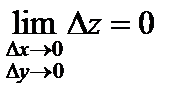, следовательно, функция непрерывна (согласно определению непрерывности функции двух переменных на языке приращений).
Теорема 2 (необходимое условие дифференцируемости).

Если функция 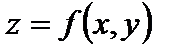дифференцируема в точке 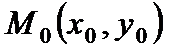, то в этой точке существуют частные производные, причём

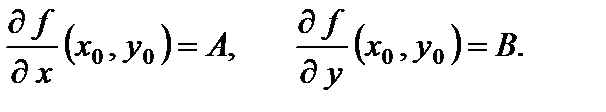
Доказательство. По условию теоремы функция 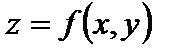дифференцируема, значит, имеет место соотношение (1). Полагая 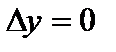, имеем, что 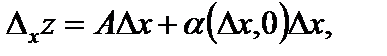где 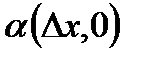─ бесконечно малая функция при .

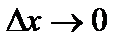Разделив на 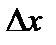и переходя к пределу при 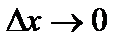, получаем

.

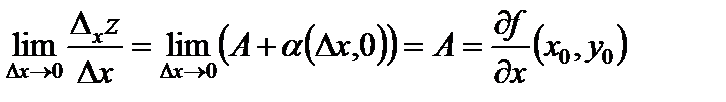ПОРЯДОК МАЛОСТИ:

Порядок малости находиться по таблице эквивалентности:

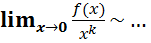незабываем ставить знак эквивалентности), k – есть порядок малости.