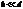Дифракция Фраунгофера на круглом отверстии.
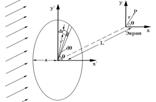 Разобьем поверхность отверстия на элементарные источники, площадь которых равна
Разобьем поверхность отверстия на элементарные источники, площадь которых равна 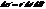 . Нужно составить комплексную амплитуду, пришедшую от
. Нужно составить комплексную амплитуду, пришедшую от 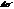 в точку
в точку 
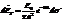 , где
, где  - разность хода лучей от
- разность хода лучей от 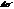 и от центра отверстия. В прямоугольной системе координат разность хода лучей записывается следующим образом
и от центра отверстия. В прямоугольной системе координат разность хода лучей записывается следующим образом 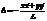 .
.
Перейдем в цилиндрическую систему координат 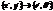 :
:
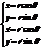

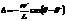 .
.
Проинтегрируем комплексную амплитуду по всей площади отверстия: 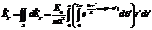 Сделав замену
Сделав замену 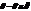 , получим следующий интеграл
, получим следующий интеграл 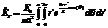 .
.
Функция 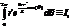 называется функцией Бесселя нулевого порядка,
называется функцией Бесселя нулевого порядка, 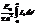 - функцией Бесселя первого порядка.
- функцией Бесселя первого порядка.
Зависимость амплитуды колебаний в точке  от ее положения на экране следующая
от ее положения на экране следующая 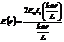 .
.
Дифракционная картина будет иметь осевую симметрию и будет представлять собой чередование светлых и темных колец.
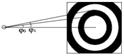
 -угловой размер пятна, видимый из отверстия.
-угловой размер пятна, видимый из отверстия.
Соответствующий расчет дает, что границы первого темного кольца отстают от центра дифракционной картины на угловые расстояния 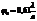 и
и 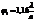 .
.
Дифракция на круглом отверстии очень заметна при работе с оптическими инструментами.
Дифракция на круглом отверстии определяет степень параллельности лазерного пучка.
Пример: Ночью по плоской степи едет машина. Оценить на каком расстоянии человек сможет различить две фары?
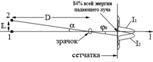
Пусть L – расстояние между фарами, D - расстояние между машиной и человеком.
Две фары видны в том случае, когда максимум интенсивности от первой фары приходится на минимум интенсивности от второй фары (условие Релея). Иначе это условие видимости можно записать следующим образом 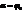 или
или 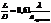 .
.
Пусть
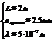 , тогда
, тогда 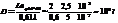 .
.
Дифракционная решетка.
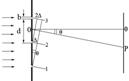 Дифракционная решетка – это спектральный прибор для изучения спектрального состава света. Она представляет собой совокупность большого числа параллельных щелей в непрозрачном экране или отражающих полосок (штрихов), расположенных параллельно друг другу на одинаковом расстоянии.
Дифракционная решетка – это спектральный прибор для изучения спектрального состава света. Она представляет собой совокупность большого числа параллельных щелей в непрозрачном экране или отражающих полосок (штрихов), расположенных параллельно друг другу на одинаковом расстоянии.
 - ширина одной щели;
- ширина одной щели;
 - расстояние между центрами щелей – период решетки (число штрихов на 1 мм);
- расстояние между центрами щелей – период решетки (число штрихов на 1 мм);
 - общее число щелей.
- общее число щелей.
Пусть падающая волна монохроматическая, и ее падение нормальное. Положение точки наблюдения  на экране описывается углом дифракции
на экране описывается углом дифракции  . Чтобы рассчитать интенсивность в точке
. Чтобы рассчитать интенсивность в точке  , надо просуммировать интенсивности от всех щелей.
, надо просуммировать интенсивности от всех щелей.
Комплексная амплитуда от 1-ой щели, в предположении, что фаза колебаний от центра 1-ой щели в точке  равна нулю, запишется так
равна нулю, запишется так 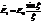 , где
, где 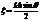 .
.
Если за начало отсчета фазы взять фазу колебаний, приходящую от центра 1-ой щели в точку 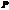 , то амплитуда от n-ой щели запишется так
, то амплитуда от n-ой щели запишется так 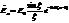 , где
, где 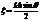 .
.
Полная амплитуда: 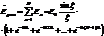 .
.
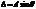 ,
,
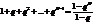 .
.
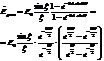
Здесь 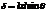 , Согласно формулам Эйлера
, Согласно формулам Эйлера 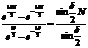 .
.
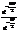 - фазовый множитель,
- фазовый множитель,
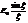 - щелевой параметр (щелевой фактор),
- щелевой параметр (щелевой фактор),
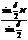 - решетчатый фактор.
- решетчатый фактор.
Зависимость интенсивности в точке  от ее расположения следующая
от ее расположения следующая 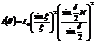
Посчитаем интенсивность в центре, для этого раскроем неопределенность вида 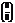 по правилу Лапиталя
по правилу Лапиталя 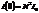 .
.
Интенсивность равна нулю, когда щелевой множитель равен нулю
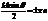

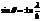 .
.
Побочные минимумы возникают, когда решетчатый фактор равен нулю
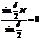

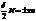

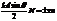

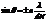 .
.
Условие главных максимумов: 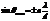 .
.
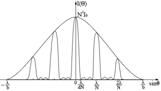
Между двумя главными максимумами существуют очень маленькие побочные максимумы. Между главными максимумами их

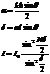
Для одной щели:
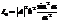 .
.
Щелевой график.
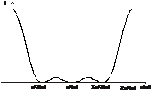
Нулевой максимум: 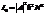 .
.
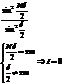
Пусть 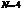 .
.
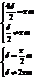
Нули функции 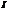 .
.
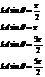
Побочных максимумов – 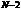 .
.
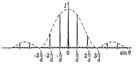
С увеличением  главные максимумы растут, и побочных становится все больше и больше, их ширина становиться все уже и уже, высота все меньше и меньше.
главные максимумы растут, и побочных становится все больше и больше, их ширина становиться все уже и уже, высота все меньше и меньше.
Дифракционную решетку можно сделать и так.
 Чем шире щель, тем уже график, чем уже щель, тем шире график.
Чем шире щель, тем уже график, чем уже щель, тем шире график.