Немонохроматические волны. Дисперсия. Групповая скорость.

1) периодическая, но другая волна



Дискретный спектр.
2) не периодическая функция



Непрерывный спектр.
Дисперсия – зависимость фазовой скорости волны от частоты.
Любой сигнал можно разложить в ряд Фурье. Он будет состоять из монохроматических волн. Дисперсия приводит к искажению монохроматической волны.
Пусть волна немонохроматическая, представляет собой сумму близких гармоник.
 Фотография волны.
Фотография волны.

Фазовые скорости разные, следовательно, возникает разность фаз, картина искажается, разность фаз будет нарастать до  , и волна восстановиться и так далее.
, и волна восстановиться и так далее.
Пусть фазовая скорость волны в среде зависит от длины волны, т.е. получили диспергирующую среду.

Т.о. если у нас есть сумма двух волн, то у них будут разные фазовые скорости, и во времени волны будут смещаться по фазе относительно друг друга. Но через определенные промежутки времени, набежит разность фаз кратная  , и тогда всё повторится.
, и тогда всё повторится.
Рассмотрим процесс распространения максимумов и минимумов в пространстве.
Пусть есть 2 волны с близкими частотами, тогда
 .
.
Будем следить за фазой максимума, т.е. когда  , т.е.
, т.е.
 .
.
 - положение фазы волны, при котором колебание имеет абсолютный максимум, тогда величина
- положение фазы волны, при котором колебание имеет абсолютный максимум, тогда величина  имеет смысл некоторой скорости, и эта величина называется групповой скоростью
имеет смысл некоторой скорости, и эта величина называется групповой скоростью
 .
.
Рассмотрим некоторую моделируемую волну, состоящую из суперпозиции многих волн.

Рассмотрим некоторый ряд Фурье. Рассмотрим много волн с конечными интервалами частот.
Если у рассматриваемой моделированной волны есть резкий пик, то при разложении в ряд Фурье получаем несколько пиков на графике  . Если наоборот некий долгий звук, то как правило на графике один или несколько частот.
. Если наоборот некий долгий звук, то как правило на графике один или несколько частот.
 .
.
Избавляясь от начальной фазы  введением комплексной амплитуды
введением комплексной амплитуды  . Тогда
. Тогда
 .
.
Чтобы взять интеграл разложим  в ряд вблизи
в ряд вблизи 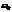 :
:
 .
.
Ограничимся в разложении линейной составляющей. Тогда:
 .
.
Так можно сделать только если  или
или  - очень мала, т.е. узкий пик. Тогда:
- очень мала, т.е. узкий пик. Тогда:
 .
.
Введём обозначение  . Тогда:
. Тогда:
 .
.
 и
и  - числа, а интегрирование идёт по
- числа, а интегрирование идёт по  , то есть можно выполнить следующее преобразование:
, то есть можно выполнить следующее преобразование:
 .Т.о. чтобы найти групповую скорость нужно проследить за максимумом модуляционной части, а она максимальна, когда показатель экспоненты равен нулю, т.е.
.Т.о. чтобы найти групповую скорость нужно проследить за максимумом модуляционной части, а она максимальна, когда показатель экспоненты равен нулю, т.е.
 ,
,
откуда (т.к.  при
при  )
)
 ,
,
 - скорость с которой бежит модуляционная часть.
- скорость с которой бежит модуляционная часть.
Так определить групповую скорость можно только при малости пика или линейности  .
.
Пусть при  имеем
имеем  . Откуда
. Откуда
 .
.
 , где
, где  - длина волны,
- длина волны,  . Тогда
. Тогда
 .
.
Вектор Умова-Поинтинга.
Вектор Умова характеризует перенос энергии в упругой волне, постараемся ввести аналог для электромагнитной волны.
Рассмотрим кусок среды (магнетик, диэлектрик и проводник, но не ферромагнетик). Пусть течёт ток с некоторой плотностью тока  , меняется индукция и магнитное поле: т.е.
, меняется индукция и магнитное поле: т.е.  .
.
Пусть также кусочек мал настолько, что нигде нет зависимоти от координат.
Найдём работу при изменении тока, поляризованности, намагниченности и т.д.
 .
.
Где  - это некоторая работа (пишем
- это некоторая работа (пишем 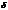 - т.к. это функция процесса, а не состояния),
- т.к. это функция процесса, а не состояния),  - индукция внешнего поля,
- индукция внешнего поля,  - поле в образце.
- поле в образце.
Пусть эта работа совершается за время  , перейдём к мощности.
, перейдём к мощности.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
Но  . Откуда:
. Откуда:
 .
.
Но т.к. все рассмотренные силы – внутренние для рассмотренного кусочка, то

 .
.
 - плотность потока энергии электромагнитного поля. Данное выражение справедливо всегда, т.к. был рассмотрен общий случай.
- плотность потока энергии электромагнитного поля. Данное выражение справедливо всегда, т.к. был рассмотрен общий случай.
В плоской электромагнитной волне  и
и  , т.е. они образуют правую тройку векторов.
, т.е. они образуют правую тройку векторов.

