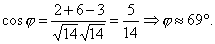Плоскость в пространстве. (Различные виды уравнений плоскости, угол между

Плоскостями.)

??? Плоскость в пространстве

План лекции

1. Уравнение плоскости. Полное и неполные уравнения плоскости.

2. Частные случаи уравнения плоскости.

3. Нормальное уравнение плоскости. Расстояние от точки до плоскости.

4. Взаимное расположение двух плоскостей в пространстве.

1. Уравнение плоскости. Полное и неполные уравнения плоскости.

Всякая плоскость в пространстве, снабженном декартовой системой координат, есть множество вех точек, удовлетворяющих некоторому линейному уравнению вида:

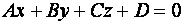(1)

Обратно, множество всех точек 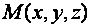,являющихся решениями произвольного уравнения (1), есть плоскость.

(1) – общее уравнение плоскости.

Пусть точка 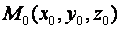лежит в плоскости (1), тогда выполняется равенство: 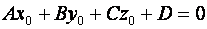(2)

Вычтем (2) из (1):

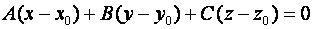
Следовательно, векторы 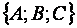и 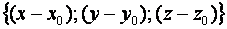ортогональны. Таким образом, вектор 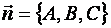является нормалью к плоскости (1) и называется нормальным вектором плоскости.

Неполные уравнения плоскости:

А) 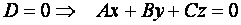- уравнение плоскости, проходящей через начало координат;

Б) 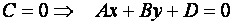- уравнение плоскости, параллельной оси ;

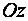В) 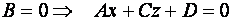- уравнение плоскости, параллельной оси ;

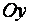Г) 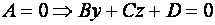- уравнение плоскости, параллельной оси ;

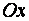Д) 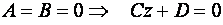- уравнение плоскости, параллельной координатной плоскости ;

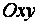Е) 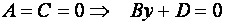- уравнение плоскости, параллельной координатной плоскости ;

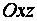Ж) 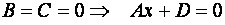- уравнение плоскости, параллельной координатной плоскости .

2. Частные случаи уравнения плоскости.

Всякую плоскость в пространстве можно задать, указав какую – ни будь ее точку 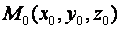и два произвольных приложенных к этой точке неколлинеарных вектора:

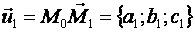и .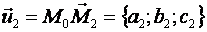

Прилагая векторы 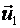и 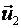к точке 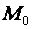, получим всевозможные закрепленные векторы вида 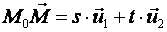, где 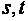- произвольные вещественные числа; концы 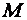этих векторов и заполняют плоскость, проходящую через точку 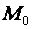и два приложенных к ней вектора .

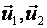В координатной форме уравнение (3) записывается так:

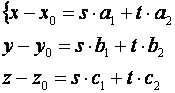(4)

(4) – параметрическое уравнение плоскости.

Уравнение (4) выражают линейную зависимость столбцов матрицы

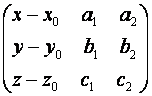
Что эквивалентно равенству:

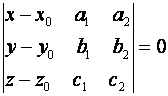(5)

Пример. Найти уравнение плоскости, проходящей через три данные точки: ; ; .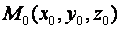

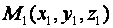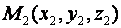Решение. Искомая плоскость содержит точку 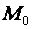и неколлинеарные векторы:

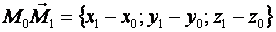и 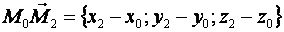, следовательно, ее уравнение можно записать в виде (5):

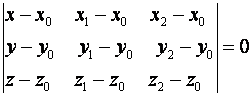
Если все коэффициенты уравнения (1) отличны от нуля, тогда его можно записать в виде:

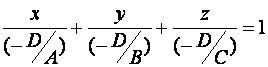
Или

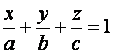(6)

Где ; ; .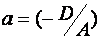

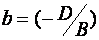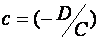(6) – уравнение плоскости в отрезках, т.к. числа 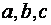- алгебраические значения отрезков, отсеченных плоскостью (1) на осях координат.

3. Нормальное уравнение плоскости. Расстояние от точки до плоскости.

Пусть дана плоскость 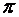. Проведем через начало координат прямую 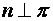, будем называть эту прямую нормалью; точка 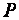- пересечение плоскости 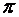и нормали 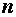. Обозначим через 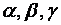углы, которые составляет вектор 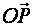с осями координат; 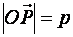. Выведем уравнение плоскости 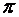, считая известными 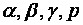. Для этого возьмем на плоскости 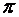произвольную точку 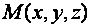, тогда 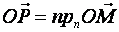, отсяда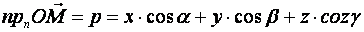

Или

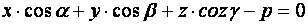(7)

(7) – нормальное уравнение плоскости.

Теорема. Расстояние 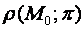от точки 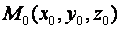до плоскости 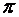вычисляется по формуле:

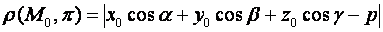
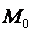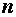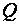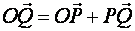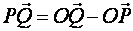Доказательство. Спроектируем точку на нормаль ; - ее проекция, тогда или , но 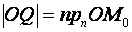; 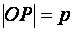, следовательно,

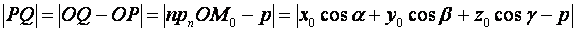
Теорема доказана.

Если плотность 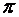задана общим уравнением (1), то расстояние от точки 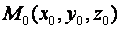до этой плоскости находится по формуле:

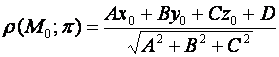
4. Взаимное расположение двух плоскостей в пространстве.

Пусть в пространстве даны две плоскост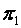и и :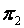

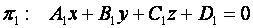
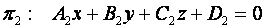
Соответствующие им векторы нормали имеют вид

,

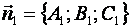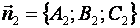
Плоскости в пространстве могут быть параллельны, совпадать, перпендикулярны и, наконец, пересекаться под произвольным углом.

Рассмотрим эти случаи.

А) Плоскост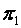и и 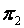параллельны, следовательно, 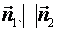, т.е. .

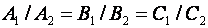Б) Плоскости и совпадают, следовательно, уравнения, их описывающие, эквивалентны, т.е. .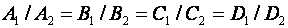

В) Плоскости пересекаются под прямым углом, тогда и 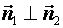, т.е. .

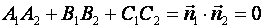Г) Плоскости пересекаются под произвольным углом; найдем этот угол. За угол между плоскостями принимается угол 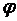между любыми двумя перпендикулярными к ним векторами, следовательно, это будет угол между нормалям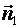и и 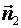, а его можно вычислить по формуле:

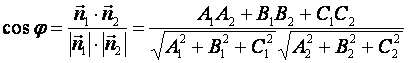
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α₁ и α₂, заданные соответственно уравнениями:

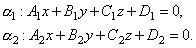
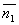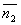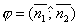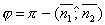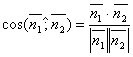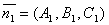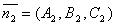Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α₁ и α₂ равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

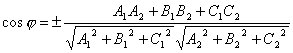Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.