Матрицы. Линейные операции над матрицами. Умножение матриц.

Матрицей размерности m × n называется прямоугольная

таблица чисел, содержащая m строк и n столбцов. Числа, обра-

зующие матрицу, называются ее элементами.

олбце.

Если у матрицы число строк равно числу столбцов и равно n ,

то она называется квадратной матрицей n -го порядка. Элемен-

ты ii

a , где i = 1,2,K, n , квадратной матрицы называются диаго-

нальными и образуют главную диагональ матрицы.

Единичной называется квадратная матрица, у которой на

главной диагонали находятся единицы, а в остальных позици-

ях — нули.Трапециевидной называется матрица, содержащая нули под

элементами a11

, a22

, a33

,...:

Элементарными преобразованиями матрицы называются

операции:

1. транспонирование матрицы;

2. перестановка двух любых строк или столбцов местами;

3. умножение элементов строки или столбца на число отлич-

ное от нуля;

4. прибавление к элементам одной строки (столбца) соответ-

ствующих элементов другой строки (столбца), умноженных

на одно и тоже число;

5. вычеркивание одной из двух пропорциональных (равных)

строк;

6. вычеркивание нулевой строки.

Матрицы, полученные одна из другой с помощью элементар-

ных преобразований, будем называть эквивалентными и обозна-

чать A ~ B

умножение

ЗАМЕЧАНИЕ 1

Произведение матрицы A на матрицу B определено только в

том случае, если число столбцов матрицы A равно числу

строк матрицы B . При этом число строк матрицы C = A⋅B

будет равно числу строк матрицы A, а число столбцов – числу

столбцов матрицы B

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля(например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических илидифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Матрицы допускают следующие алгебраические операции:

§ сложение матриц, имеющих один и тот же размер;

§ умножение матриц подходящего размера (матрицу, имеющую n столбцов, можно умножить справа на матрицу, имеющую n строк);

§ умножение матрицы на элемент основного кольца или поля (т. е. скаляр).

Сложение матриц

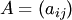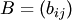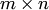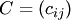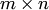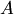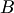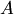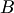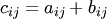
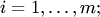
Пусть и — матрицы одинаковых размеров . Матрица тех же размеров называется суммой матриц и , если ее элементы равны сумме соответствующих элементов матриц и : 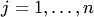. Сумма матриц обозначается .

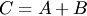Из определения следует, что складывать можно только матрицы одинаковых размеров.

Умножение матрицы на число

Произведением матрицы 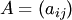на число 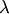называется матрица 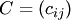тех же размеров, что и матрица 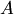, каждый элемент которой равен произведению числа 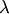на соответствующий элемент матрицы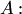

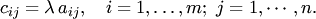
Произведение обозначается 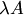или .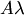

Умножить на число можно любую матрицу, при этом каждый ее элемент умножается на это число.

5. Модели планирования производства.

????????