Понятие функции. Предел функции в точке.
Понятие функции
Пусть х и у - некоторые числовые множества, и пусть каждому числовому значению переменной х из множества Х по заданному закону соответствует числовое значение переменной у из множества У, то говорят, что функция определена у=f(x).
Х называется независимой переменной (аргументом), у - зависимой переменной, множество Х - область определения, У - область значений функции y=f(x).
Предел функции в точке
Пусть функция f(x) определив в некоторой окрестности точки х=а (то есть в самой точке х=а функция может быть и не определена).
Число А называется пределом функции f(x) при х->а, если для любого епсилон>0 существует такое число дельта>0, что для всех х таких, что |х^н-а|< дельта верно неравенство |f(x)-A|< епсилон.
То же определение может быть записано в другом виде:
Если а-дельта<х<а+дельта, х!=а, то верно неравенство А-епсилон<f(x)<A+епсилон
Если f(x)->A1 при х->a только при х<a, то - называется приделом функции f(x) в точке х=а слева, а если f(x)->A2 при х->а только при х>a, то называется пределом функции f(x) в точке х=a справа.
Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х=a.
Предел функции при стремлении аргумента к бесконечности
Число А называется пределом функции f(x) при х стремится к бесконечности, если функция f(x) определена в окрестности бесконечности и для любого числа епсилон>0 существует такое число М>0, что для всех х, |х|>М выполняется неравенство |f(x)-A|<епсилон. Записывают: lim x->бесконечности f(x)=A.
Основные теоремы о пределах
Теорема 1. Если С=const, то lim x->a C=C.
Пусть функции f(x) и g(x) имеют конечные пределы при х->а lim x->a f(x) lim x->a g(x), тогда имеют место следующие
теоремы:
Теорема 2. Lim x->a C * f(x)= C*lim x->a f(x)
Теорема 3. Lim x->a (f(x)+/-g(x))=lim x->a f(x) +/- lim x->a g(x).
Теорема 4. Lim x->a [f(x)*g(x)]=lim x->a f(x) * lim x->a g(x).
Теорема 5. Lim x->a f(x)/g(x)=lim f(x)/lim g(x) при lim g(x)!=0.
Теорема 6. Если f(x)>0 вблизи точки х=а и lim f(x)=A, то А>0, аналогично ппри f(x)<0, f(x)>=0, f(x)<=0.
Теорема 7. Если g(x)<=f(x)<=u(x) вблизи точки х=а и lim g(x)=lim u(x)=A, то lim f(x)=A.
Функция f(x) называется ограниченной вблизи точки х=а, если существует такое число М>0, что |f(x)|<M вблизи точки х=а.
Теорема 8. Если функция f(x) имеет конечный предел при х->а, то она ограничена вблизи точки х=а.
Доказательство: пусть lim f(x)=A, |f(x)-A|<e,
|f(x)|=|f(x)-A+A|<=|f(x)-A|+|A| или |f(x)|<e+|A|, то есть М=е+|А|.
Некоторые замечательные пределы.
- Первый замечательный предел:
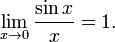
- Второй замечательный предел:
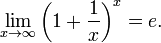
Понятие бесконечно малых функций и их св-ва.
Бесконечно малая — числовая функция, которая стремится к нулю.
Функция называется бесконечно малой в окрестности точки x0, если 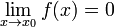 .
.
Функция называется бесконечно малой на бесконечности, если 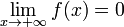 либо
либо 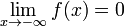 .
.
Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если 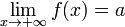 , то f(x) − a = α(x),
, то f(x) − a = α(x), 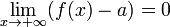 .
.
