Предел ЧП. Теоремы о пределах.
Модуль числа
Модулем неотрицательного действительного числа a называют само это число: |а| = а
Модулем отрицательного действительного числа aназывают противоположное число: |а| = - а.
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).
Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули: |-а| = |а|
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета 0, т.е. удалена от нее на 0 единичных отрезков: |0| = 0
На практике используют различные свойства модулей:
|а| ≥ 0
|а·b| = |а| · |b|
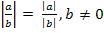
|а|n= аn, n є Z, a ≠ 0, n > 0
|а| = | - а|
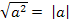
|а + b| ≤ |а| + |b|
|а·q| = q·|а| , где q - положительное число
|а|2= а2
ЧП
Если каждому натуральному числу н поставлено в соответствие число хн, то говорят, что задана последовательность х1, х2,...,хн={хн}
Для последовательностей можно определить следующие операции:
1) умножение последовательности на число м: м{хн}={мхн}, то есть мх1, мх2,...,мхн
2) сложение (вычитание) последовательностей: {хн}+/-{ун}={хн+/-ун}
3) произведение последовательностей: {хн}*{ун}={хн*ун}
4) частное последовательностей: {хн}/{ун}, при ун=0
Последовательность{хн} называется ограниченной, если существует такое число М>0 (М - конечное число), что для любого н верно неравенство: |хн|<М, то есть все члены последовательности принадлежат промежутку (-М;М).
Последовательность {хн} называется ограниченной сверху, если для любого н существует такое число М, что хн<=М.
Последовательность {хн} называется ограниченной снизу, если для любого н существует такое число М, что хн>=М.
Предел ЧП. Теоремы о пределах.
Число а называется пределом последовательности {хн}, если для любого положительного числа епсилон>0 существует такой номер N, что для всех номеров н>N выполняется условие: |хн - а|<епсилон.
Это записывается: lim хн=а или хн->а.
Говорят, что {хн} сходится к числу а при н-> бесконечность
Свойство: если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.
Последовательность без придела - расходящаяся.
Теорема:
Последовательность не может иметь более одного предела.
Доказательство:
предположим, что последовательность {хн} имеет два предела а и б, не равные друг другу, то есть хн->а; хн->б; а!=б.
Тогда по определению существует такое число епсилон>0, что:
|а-хн|< епсилон/2; |б-хн|<епсилон/2; х принадлежит (а-епсилон/2, а+епсилон/2), (б-епсилон/2,б+епсилон/2).
Выполним оценку:
|а-б|=|(а-хн)+(хн-б)|<=|а-хн|+|хн-б|<епсилон/2+епсилон/2=епсилон.
Так как епсилон - любое число, то |а-б|=0, то есть а=б.
|а-б|<епсилон.
Теорема. Если хн->а, то последовательность {хн} ограничена. А - конечное число.
Обратное утверждение не верно, то есть из ограниченной последовательности не следует ее сходимость.
Монотонные последовательности:
1) если хн+1>хн для всех н, то последовательность возрастающая;
2) если хн+1>=хн для всех н, то последовательность неубывающая.
3) если хн+1<хн для всех н, то последовательность убывающая;
4) если хн+1<=хн для всех н, то последовательность невозрастающая.
Возрастающие и убывающие последовательности называются строго монотонными.
Пример: {хн}=1/н - убывающая и ограниченная, н-> бесконечность, 1/н ->0. {хн}=н - возрастающая и неограниченная.
Теорема. Монотонная ограниченная последовательность имеет предел.
Понятие функции
Пусть х и у - некоторые числовые множества, и пусть каждому числовому значению переменной х из множества Х по заданному закону соответствует числовое значение переменной у из множества У, то говорят, что функция определена у=f(x).
Х называется независимой переменной (аргументом), у - зависимой переменной, множество Х - область определения, У - область значений функции y=f(x).
Предел функции в точке
Пусть функция f(x) определив в некоторой окрестности точки х=а (то есть в самой точке х=а функция может быть и не определена).
Число А называется пределом функции f(x) при х->а, если для любого епсилон>0 существует такое число дельта>0, что для всех х таких, что |х^н-а|< дельта верно неравенство |f(x)-A|< епсилон.
То же определение может быть записано в другом виде:
Если а-дельта<х<а+дельта, х!=а, то верно неравенство А-епсилон<f(x)<A+епсилон
Если f(x)->A1 при х->a только при х<a, то - называется приделом функции f(x) в точке х=а слева, а если f(x)->A2 при х->а только при х>a, то называется пределом функции f(x) в точке х=a справа.
Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х=a.
Предел функции при стремлении аргумента к бесконечности
Число А называется пределом функции f(x) при х стремится к бесконечности, если функция f(x) определена в окрестности бесконечности и для любого числа епсилон>0 существует такое число М>0, что для всех х, |х|>М выполняется неравенство |f(x)-A|<епсилон. Записывают: lim x->бесконечности f(x)=A.
Основные теоремы о пределах
Теорема 1. Если С=const, то lim x->a C=C.
Пусть функции f(x) и g(x) имеют конечные пределы при х->а lim x->a f(x) lim x->a g(x), тогда имеют место следующие
теоремы:
Теорема 2. Lim x->a C * f(x)= C*lim x->a f(x)
Теорема 3. Lim x->a (f(x)+/-g(x))=lim x->a f(x) +/- lim x->a g(x).
Теорема 4. Lim x->a [f(x)*g(x)]=lim x->a f(x) * lim x->a g(x).
Теорема 5. Lim x->a f(x)/g(x)=lim f(x)/lim g(x) при lim g(x)!=0.
Теорема 6. Если f(x)>0 вблизи точки х=а и lim f(x)=A, то А>0, аналогично ппри f(x)<0, f(x)>=0, f(x)<=0.
Теорема 7. Если g(x)<=f(x)<=u(x) вблизи точки х=а и lim g(x)=lim u(x)=A, то lim f(x)=A.
Функция f(x) называется ограниченной вблизи точки х=а, если существует такое число М>0, что |f(x)|<M вблизи точки х=а.
Теорема 8. Если функция f(x) имеет конечный предел при х->а, то она ограничена вблизи точки х=а.
Доказательство: пусть lim f(x)=A, |f(x)-A|<e,
|f(x)|=|f(x)-A+A|<=|f(x)-A|+|A| или |f(x)|<e+|A|, то есть М=е+|А|.
Понятие производной.
Пусть функция 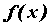 определена на промежутке
определена на промежутке 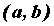 . Точка
. Точка 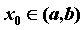 — произвольная точка из области определения функции,
— произвольная точка из области определения функции, 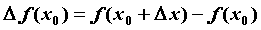 — приращение функции в точке
— приращение функции в точке 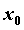 , вызванное приращением
, вызванное приращением 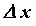 независимой переменной
независимой переменной 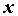 Производнойфункции
Производнойфункции 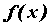 по независимой переменной
по независимой переменной 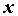 в точке
в точке 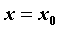 ,
, 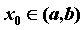 называется предел отношения приращения функции
называется предел отношения приращения функции 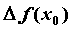 к приращению
к приращению 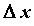 при стремлении
при стремлении 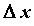 к нулю, т.е.
к нулю, т.е.
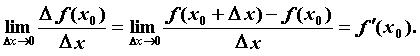
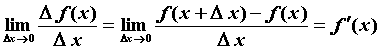 ,
,
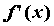 — производная функции в точке
— производная функции в точке 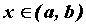 .
.
Правила дифференцирования.
Пусть функция 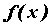 определена в некоторой окрестности точки
определена в некоторой окрестности точки 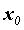 . Рассмотрим приращение функции в этой точке:
. Рассмотрим приращение функции в этой точке: 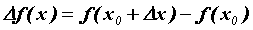 . Функция
. Функция 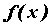 называется дифференцируемой в точке , если ее приращение можно записать в виде
называется дифференцируемой в точке , если ее приращение можно записать в виде 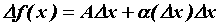 , где
, где 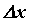 - приращение независимой переменной, А – постоянная, не зависящая от
- приращение независимой переменной, А – постоянная, не зависящая от 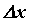 ,
, 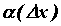 - бесконечно малая функция при
- бесконечно малая функция при 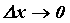 .
.
Дифференциалом функции 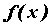 в точке
в точке 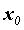 называется линейная по
называется линейная по 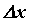 часть
часть 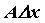 приращения
приращения 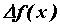 . Дифференциал обозначается
. Дифференциал обозначается 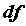 , то есть
, то есть 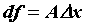 . Рассматривая функцию
. Рассматривая функцию 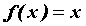 , нетрудно убедиться, что
, нетрудно убедиться, что 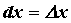 , если
, если 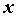 - независимая переменная.
- независимая переменная.
Воспользуемся определением производной для дифференцируемой функции 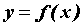 в точке
в точке 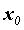 :
: 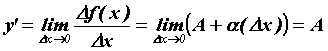 . Таким образом, дифференциал функции выражается формулой
. Таким образом, дифференциал функции выражается формулой 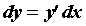 , то есть для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на
, то есть для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на 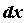 . Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке существовала конечная производная.
. Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке существовала конечная производная.
Таблица производных.
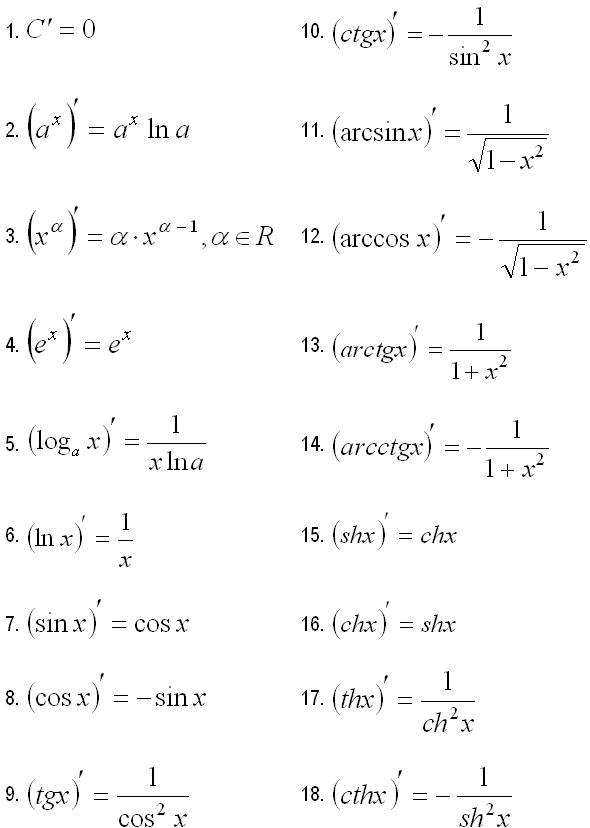
Производные сложных функций
Пусть функция 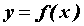 дифференцируема и строго монотонна на
дифференцируема и строго монотонна на 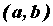 . Пусть также в точке
. Пусть также в точке 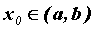 производная
производная 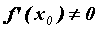 . Тогда в точке
. Тогда в точке 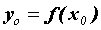 определена дифференцируемая функция
определена дифференцируемая функция 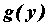 , которую называют обратной к
, которую называют обратной к 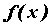 , а ее производная вычисляется по формуле
, а ее производная вычисляется по формуле 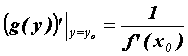 .
.
Дифференциал функции.
Дифференциалом функции 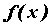 в точке
в точке 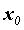 называется линейная по
называется линейная по 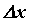 часть
часть 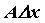 приращения
приращения 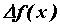 . Дифференциал обозначается
. Дифференциал обозначается 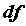 , то есть
, то есть 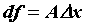 . Рассматривая функцию
. Рассматривая функцию 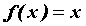 , нетрудно убедиться, что
, нетрудно убедиться, что 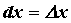 , если
, если 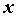 - независимая переменная.
- независимая переменная.
Теорема Ферма.
Теорема утверждает, что:
Для любого натурального числа n > 2уравнение 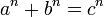 не имеет натуральных решений a, b и c. не имеет натуральных решений a, b и c. |
Теорема Ролля.
Теорема Ро́лля (теорема о нуле производной) утверждает, что Если функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
Теорема Лагранжа.
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция f непрерывна на отрезке[a;b] и дифференцируема в интервале (a;b), то найдётся такая точка 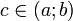 , что
, что
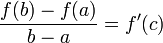 .
.
Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Механическое истолкование: Пусть f(t) — расстояние точки в момент t от начального положения. Тогда f(b) − f(a) есть путь, пройденный с момента t = a до момента t = b, отношение 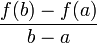 — средняя скорость за этот промежуток.
— средняя скорость за этот промежуток.
Теорема Коши.
Пусть функции f(x) и g(x)
- непрерывны на отрезке [a, b];
- дифференцируемы в интервале (a, b);
| f '(c) |
| g '(c) |
- "x О (a, b) g'(x) ≠ 0 .
| |
| g(b) − g(a) |
Тогда существует точка c О (a, b) такая, что
Правило Лопиталя.
Правило Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и 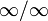 . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Условия:
1. 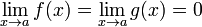 или
или 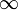 ;
;
2. 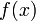 и
и 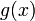 дифференцируемы в проколотой окрестности
дифференцируемы в проколотой окрестности 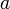 ;
;
3. 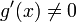 в проколотой окрестности
в проколотой окрестности 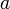 ;
;
4. существует 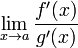 ,
,
тогда существует 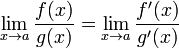 .
.
Пределы также могут быть односторонними.
Экстремумы Функции.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.
Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f ¢(xо) = 0, либо f ¢(xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
Первое достаточное условие. Пусть xо - критическая точка. Если f ¢ (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе достаточное условие. Пусть функция f(x) имеет производную
f ¢ (x) в окрестности точки xо и вторую производную 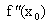 в самой точке xо. Если f ¢(xо) = 0,
в самой точке xо. Если f ¢(xо) = 0, 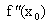 >0 (
>0 ( 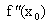 <0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же
<0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же 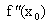 =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Точки перегиба.
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
Асимптота — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность.
Вертикальная
Вертикальная асимптота — прямая вида 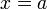 при условии существования предела
при условии существования предела 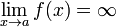 .
.
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
1. 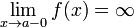
2. 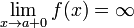
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.
Горизонтальная
Горизонтальная асимптота — прямая вида 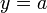 при условии существования предела
при условии существования предела
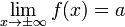 .
.
Наклонная
Наклонная асимптота — прямая вида 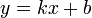 при условии существования пределов
при условии существования пределов
1. 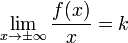
2. 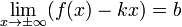
35)Схема исследования функции.
1. Область определения
2. Исследование функции на четность, нечетность и периодичность
Если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство 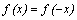 , то
, то 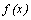 – четная функция; если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство
– четная функция; если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство 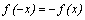 , то
, то 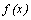 – нечетная функция; в противном случае,
– нечетная функция; в противном случае, 
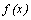 – общего вида. График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
– общего вида. График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
3. Нахождение точек пересечения графика функции с осями координат
Точки пересечения с осью ОХ: 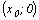 , где
, где 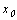 – решение уравнения
– решение уравнения 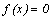 .
.
Точки пересечения с осью ОY: 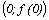 .
.
4. Нахождение промежутков знакопостоянства функции
Промежутки знакопостоянства функции – промежутки из области определения функции, где функция принимает положительные или отрицательные значения, т.е. 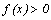 или
или 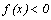 .
.
5. Нахождение производной функции, области определения производной, критических точек
Критические точки функции – внутренние точки области определения функции, в которых производная не существует или равна нулю.
6. Нахождение промежутков возрастания, убывания, точек экстремума и экстремумов
Критические точки функции разбивают область определения функции на промежутки. Для нахождения промежутков возрастания, убывания и точек экстремума нужно определить знак производной на каждом из полученных промежутков. Если производная функции положительна на некотором промежутке I, то функция возрастает на этом промежутке; если производная функции отрицательна на некотором промежутке I, то функция убывает на этом промежутке. Если при переходе через критическую точку производная меняет знак, то данная точка является точкой экстремума.
7. Нахождение промежутков выпуклости функции и точек перегиба
Для нахождения промежутков выпуклости используется вторая производная функции. Точки, в которых вторая производная равна нулю или не существует, разбивают область определения функции на промежутки. Если вторая производная на полученном промежутке положительна, то график функции имеет выпуклость вниз, если – отрицательна, то график функции имеет выпуклость вверх. Если при переходе через точку, в которой вторая производная равна нулю или не существует, вторая производная меняет знак, то данная точка является точкой перегиба.
8. Исследование поведения функции на бесконечности и в окрестности точек разрыва
Для исследования поведения функции в окрестности точки разрыва 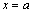 необходимо вычислить односторонние пределы:
необходимо вычислить односторонние пределы: 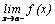 и
и 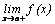 . Если хотя бы один из данных пределов равен бесконечности, то говорят, что прямая
. Если хотя бы один из данных пределов равен бесконечности, то говорят, что прямая 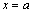 – вертикальная асимптота.
– вертикальная асимптота.
При исследовании поведения функции на бесконечности необходимо проверить, не имеет ли график функции наклонных асимптот при 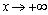 и
и 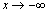 . Для этого нужно вычислить следующие пределы:
. Для этого нужно вычислить следующие пределы: 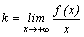 и
и 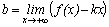 . Если оба предела существуют, то
. Если оба предела существуют, то 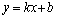 – уравнение наклонной асимптоты при
– уравнение наклонной асимптоты при 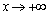 . Частный случай наклонной асимптоты при
. Частный случай наклонной асимптоты при 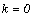 – горизонтальная асимптота. Аналогично ищется наклонная асимптота при
– горизонтальная асимптота. Аналогично ищется наклонная асимптота при 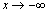 .
.
9. Построение графика (при необходимости нужно найти значения функции в дополнительных точках).
Таблица интегралов.
| 1. | 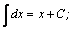 | 11. | 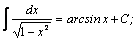 |
| 2. | 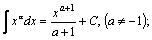 | 12. | 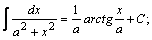 |
| 3. | 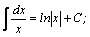 | 13. | 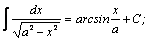 |
| 4. | 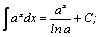 | 14. | 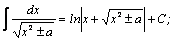 |
| 5. | 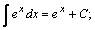 | 15. | 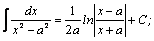 |
| 6. | 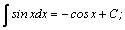 | 16. | 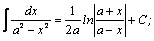 |
| 7. | 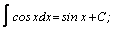 | 17. | 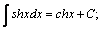 |
| 8. | 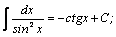 | 18. | 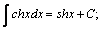 |
| 9. | 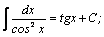 | 19. | 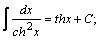 |
| 10. | 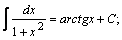 | 20. | 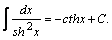 |
Определённый интеграл.
Пусть функция f(x) определена на отрезке [a, b]. Разобьем отрезок [a, b ] на n отрезков точками
| x0 = a < x1 < … < xk − 1 < xk < … < xn − 1 < xn = b |
и введем обозначения
Δxk = xk − xk − 1 (k = 1, …,n); λ =
Δxk. |
На каждом отрезке [x k − 1, x k] выберем произвольным образом точку ξk (k = 1, …,n) и составим сумму
f(ξk) · Δxk , | (5) |
называемую (римановой) интегральной суммой функции f(x) на отрезке [a, b ].
Если существует конечный предел интегральных сумм (5) при λ → 0, причем этот предел не зависит ни от способа разбиения отрезка [a , b] на части, ни от выбора точек ξk, то функция f(x) называется интегрируемой (по Риману) на отрезке [a, b ], а указанный предел называется (римановым) определенным интегралом от f(x) по отрезку [a, b ] и обозначается символом
f(x) dx . |
Таким образом,
f(x) dx =
f(ξk) · Δxk . |
Замечание. Данное Риманом определение интеграла оказалось неудачным. Современная терия интегрирования опирается на определение, данное Лебегом. Она гораздо более мощная и простая в применениях, чем теория Ремана.
3. Необходимое условие интегрируемости
Теорема 1. Если функция f(x) интегрируема на отрезке [a, b], то она ограничена на этом отрезке.
Доказательство приведено в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова “Курс высшей математики : Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения”. М. : Изд–во МЭИ, 2002. (Стр. 41.)
Замечание. Ограниченность функции не является достаточным условием ее интегрируемости.
Формула Ньютона-Лейбница.
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Если 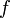 непрерывна на отрезке
непрерывна на отрезке 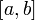 и
и 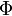 — ее любая первообразная на этом отрезке, то имеет место равенство:
— ее любая первообразная на этом отрезке, то имеет место равенство:
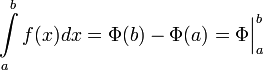
52)Формула замены переменной в определённом интеграле.
Определенный интеграл 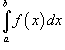 по переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t):
по переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t):
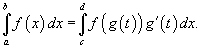
Новые пределы интегрирования по переменной t определяются выражениями
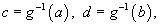
где g -1 - обратная функция к g, т.е. t = g -1(x).
Предел и непрерывность ФНП.
Число А называется пределом функции нескольких переменных f 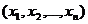 в точке М0, если
в точке М0, если 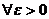
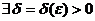 такое, что | f(M) – A| < ε для любой точки М из δ-окрестности М0.
такое, что | f(M) – A| < ε для любой точки М из δ-окрестности М0.
Функция f 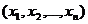 называется непрерывной в точке М0
называется непрерывной в точке М0 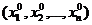 , если
, если 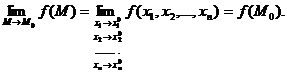 .
.
Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных 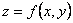 в точке
в точке 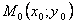 частные производные определяются так:
частные производные определяются так:
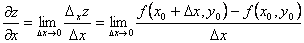 ,
,
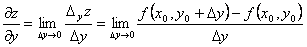 .
.
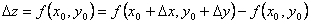 . (1)
. (1)
Если приращение (1) можно представить в виде 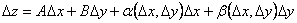 , (2)
, (2)
Где Аи В не зависят от 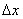 и
и 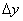 , а
, а 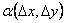 и
и 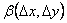 стремятся к нулю при стремлении к нулю
стремятся к нулю при стремлении к нулю 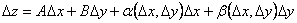
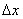 и
и 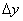 , то функция
, то функция 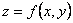 называется дифференцируемой в точке
называется дифференцируемой в точке 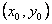 , а линейная часть
, а линейная часть 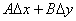 приращения функции (т.е. та часть
приращения функции (т.е. та часть 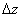 , которая зависит от
, которая зависит от 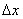 и
и 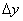 линейно) называется полным дифференциалом (или просто дифференциалом) этой функции в точке
линейно) называется полным дифференциалом (или просто дифференциалом) этой функции в точке 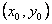 и обозначается символом
и обозначается символом 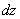 :
:
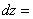
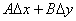 . (3)
. (3)
Из определения дифференцируемости функции следует, что если данная функция дифференцируема в точке 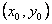 , то она в этой точке непрерывна.
, то она в этой точке непрерывна.
Производная сложной ФНП.
Пусть М(х1, х2, ..., хm) внутренняя точка области определения функции u=f(x1, ..., xm). Пусть  xk - приращение k-ой координаты в данной фиксированной т.М, ему соответствует частное приращение функции
xk - приращение k-ой координаты в данной фиксированной т.М, ему соответствует частное приращение функции
 xku
xku  f(x1, ..., xk-1, xk +
f(x1, ..., xk-1, xk +  xk, xk+1, ..., xm) - f(x1, ..., xm).
xk, xk+1, ..., xm) - f(x1, ..., xm).
Рассмотрим отношение 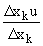 , которое зависит от
, которое зависит от  xk и определено при всех достаточно малых
xk и определено при всех достаточно малых  xk, отличных от нуля.
xk, отличных от нуля.
Определение 1. Если существует 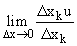 , то он называется частной производной функции u=f(x1, ..., xm) в т. М(x1, ..., xm) по аргументу xk и обозначается одним из символов:
, то он называется частной производной функции u=f(x1, ..., xm) в т. М(x1, ..., xm) по аргументу xk и обозначается одним из символов: 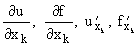 . Таким образом,
. Таким образом, 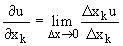 .
.
Замечание.Так как изменяется только xk +  xk, т.е. k-я координата аргумента функции f, то частная производная
xk, т.е. k-я координата аргумента функции f, то частная производная 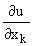 является обыкновенной производной функции f как функции только k-й переменной (при фиксированных остальных переменных). Это позволяет вычислить частные производные по одной из переменных по обычным формулам дифференцирования, если зафиксировать все остальные переменные.
является обыкновенной производной функции f как функции только k-й переменной (при фиксированных остальных переменных). Это позволяет вычислить частные производные по одной из переменных по обычным формулам дифференцирования, если зафиксировать все остальные переменные.
производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.
Рассмотрим функцию 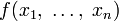 от
от 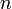 аргументов в окрестности точки
аргументов в окрестности точки 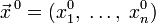 . Для любого единичного вектора
. Для любого единичного вектора 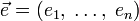 определим производную функции
определим производную функции 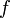 в точке
в точке 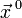 по направлению
по направлению 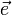 следующим образом:
следующим образом:
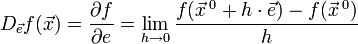
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора 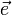 .
.
Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.
Связь с градиентом
Производную по направлению дифференциируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
Пусть задана функция f(x, y). Тогда каждая из ее частных производных(если они, конечно, существуют) 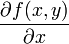 и
и 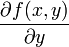 , которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная
, которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная 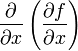 обозначается через
обозначается через 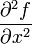 или fxx'', а
или fxx'', а 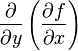 через
через 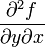 или fxy''. Таким образом,
или fxy''. Таким образом,
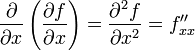 ,
, 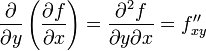
и, аналогично,
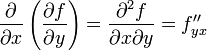 ,
, 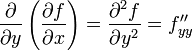 .
.
Производные fxx'',fxy'',fyx'' и fyy'' называются частными производными второго порядка. Определение:Частной производной второго порядка от функции z=f(x;y) дифференцируемой в области D,называется первая производная от соответствующей частной производной. Рассматривая частные производные от них, получим всевозможные частные производные третьего порядка: 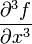 ,
, 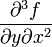 ,
, 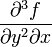 и т. д.
и т. д.
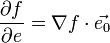 ,где
,где 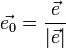 — орт направления.
— орт направления.
Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора 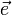 .
.
