I. Введение в математический анализ.
1. Элементы теории множеств и математической логики: понятие множества, операции над множествами, множество действительных чисел, необходимое и достаточное условия, прямая и обратная теоремы, символы математической логики и их использование.
2. Абсолютная величина действительного числа и ее свойства.
3. Функция. Область ее определения. Способы задания. Основные элементарные функции, их свойства и графики.
4. Числовая последовательность и ее предел. Ограниченная переменная.
5. Бесконечно большие и бесконечно малые величины, их свойства.
6. Теоремы о пределах. Признаки существования предела переменной.
7. Предел функции в точке. Два замечательных предела.
8. Неопределенности и их раскрытие.
9. Сравнение бесконечно малых.
10. Непрерывность функции в точке. Разрывы функции.
11. Сложная функция и ее непрерывность. Непрерывность элементарных функций.
12. Свойства функций, непрерывных на отрезке.
II. Дифференциальное исчисление функции одной переменной.
13. Производная функции в точке. Определение, ее геометрический и механический смысл. Необходимое условие дифференцируемости.
14. Производные сложной и обратной функций. Формулы и правила дифференцирования.
15. Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала. Применение дифференциала к приближенным вычислениям.
16. Производные и дифференциалы высших порядков.
17. Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа и Каши. Формулировки и доказательства.
18. Правило Лопиталя
19. Исследование функций и построение графиков.

ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
Контрольная работа №1
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
1-10.Найти пределы, не пользуясь правилом Лопиталя.
1.а) 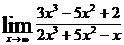 ; б)
; б) 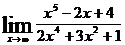 ; в)
; в) 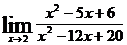 ;
;
г) 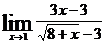 ; д)
; д) 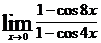 ; е)
; е) 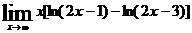
2.а) 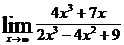 ; б)
; б) 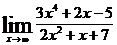 ; в)
; в) 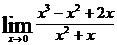 ;
;
г) 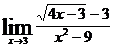 ; д)
; д) 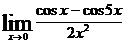 ; е)
; е) 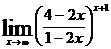 .
.
3.а) 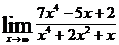 ; б)
; б) 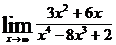 ; в)
; в) 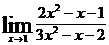 ;
;
г) 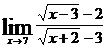 ; д)
; д) 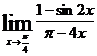 ; е)
; е) 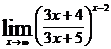 .
.
4.а) 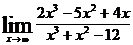 ; б)
; б) 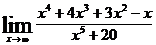 ; в)
; в) 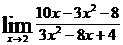 ;
;
г) 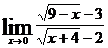 ; д)
; д) 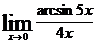 ; е)
; е) 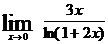 .
.
5.а) 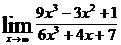 ; б)
; б) 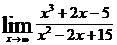 ; в)
; в) 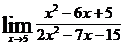 ;
;
г) 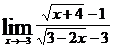 ; д)
; д) 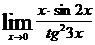 ; е)
; е) 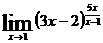 .
.
6.а) 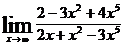 ; б)
; б) 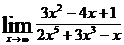 ; в)
; в) 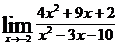 ;
;
г) 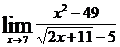 ; д)
; д) 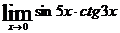 ; е)
; е) 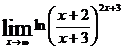 .
.
7.а) 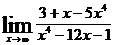 ; б)
; б) 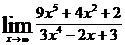 ; в)
; в) 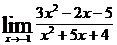 ;
;
г) 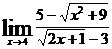 ; д)
; д) 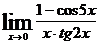 ; е)
; е) 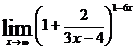 .
.
8.а) 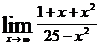 ; б)
; б) 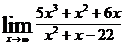 ; в)
; в) 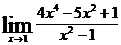 ;
;
г) 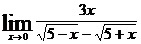 ; д)
; д) 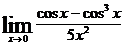 ; е)
; е) 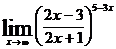 .
.
9.а) 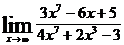 ; б)
; б) 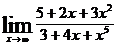 ; в)
; в) 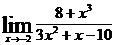 ;
;
г) 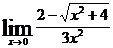 ; д)
; д) 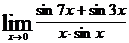 ; e)
; e) 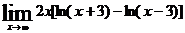
10.а) 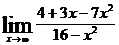 ; б)
; б) 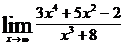 ; в)
; в) 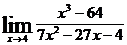 ;
;
г) 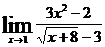 ; д)
; д) 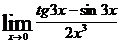 ; е)
; е) 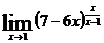 .
.
11-20.Исследовать функцию на непрерывность в указанных точках.
11. 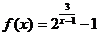 ; х1 = 1, х2 = 2.
; х1 = 1, х2 = 2.
12. 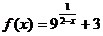 ; х1 = 2, х2 = 3.
; х1 = 2, х2 = 3.
13. 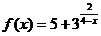 ; х1 = 2, х2 = 4.
; х1 = 2, х2 = 4.
14. 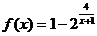 ; х1 = - 2, х2 = -1.
; х1 = - 2, х2 = -1.
15. 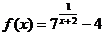 ; х1 = -3, х2 = -2.
; х1 = -3, х2 = -2.
16. 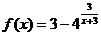 ; х1 = -3, х2 = -2.
; х1 = -3, х2 = -2.
17. 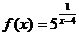 ; х1 = 2, х2 = 4.
; х1 = 2, х2 = 4.
18. 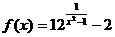 ; х1 = 1, х2 = 2.
; х1 = 1, х2 = 2.
19. 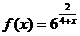 ; х1 = -5, х2 = -4.
; х1 = -5, х2 = -4.
20. 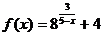 ; х1 = 4, х2 = 5.
; х1 = 4, х2 = 5.
21-30. Исследовать на непрерывность функцию, найти точки разрыва, указать характер разрыва и построить график функции y = f (x) в области определения.
 – 2x + 1 при –2 £ x£ –1,
– 2x + 1 при –2 £ x£ –1,
21. f(x) = 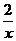 при –1 < x £ 1,
при –1 < x £ 1,
2x при 1 < x £ 2 .
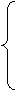 |
–x 2 при –2 £ x£ –1,
22. f(x) = 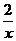 при –1 < x £ 1,
при –1 < x £ 1,
3 x–1 при 1 < x £ 2.
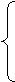 2 x 2 при –2 £ x£ 0,
2 x 2 при –2 £ x£ 0,
23. f(x) = 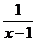 при 0 < x £ 2,
при 0 < x £ 2,
1 при 2 < x £ 3.
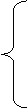 –x –2 при –2 £ x£ –1,
–x –2 при –2 £ x£ –1,
24. f(x) =  при –1 < x £ 1,
при –1 < x £ 1,
ln x при 1 < x £ e.
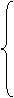 –x 2 при –2 £ x£ –1,
–x 2 при –2 £ x£ –1,
25. f(x) =  при –1 < x £
при –1 < x £ 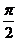 ,
,
2 sin x  при
при 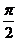 < x £
< x £ 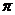 .
.
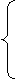 – x– 2 при –3 £ x£ –1,
– x– 2 при –3 £ x£ –1,
26. f(x) =  при –1 < x £ 2,
при –1 < x £ 2,
1 при 2 < x £ 3.
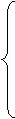
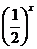 при –1 £ x£ 0,
при –1 £ x£ 0,
27. f(x) = 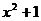 при 0 < x £ 1,
при 0 < x £ 1,
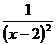 при 1 < x £ 3.
при 1 < x £ 3.
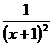 при –2 £ x£ 0,
при –2 £ x£ 0,
28. f(x) = 2x2–1 4 при 0 < x£ 1,
1 при 1 < x £ 3.
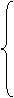 2x2 –1 при –1 £ x£ 0,
2x2 –1 при –1 £ x£ 0,
29. f(x) = 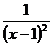 при 0 < x£ 2,
при 0 < x£ 2,
x–1 при 2 < x£ 3.
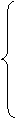 cos x при –
cos x при – 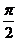 £ x< 0,
£ x< 0,
30. f(x) = 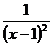 при 0 < x £ 2,
при 0 < x £ 2,
x + 1 при 2 < x£ 3.
Контрольная работа №3
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ.
31- 40.Найти производные 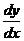 данных функций.
данных функций.
31. а) 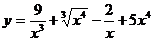 ; б)
; б) 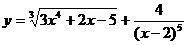 ;
;
в) 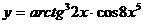 ; г)
; г) 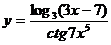 .
.
32. а) 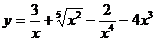 ; б)
; б) 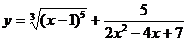 ;
;
в) 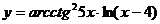 ; г)
; г) 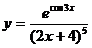 .
.
33. а) 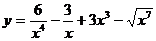 ; б)
; б) 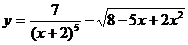 ;
;
в) 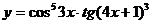 ; г)
; г) 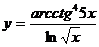 .
.
34. а) 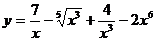 ; б)
; б) 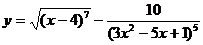 ;
;
в) 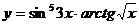 ; г)
; г) 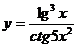 .
.
35. а) 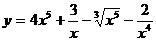 ; б)
; б) 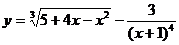 ;
;
в) 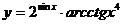 ; г)
; г) 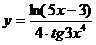 .
.
36. а) 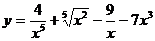 ; б)
; б) 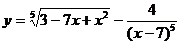 ;
;
в) 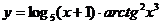 ; г)
; г) 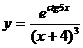 .
.
37. а) 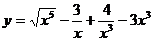 ; б)
; б) 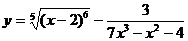 ;
;
в) 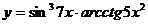 ; г)
; г) 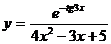 .
.
38. а) 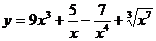 ; б)
; б) 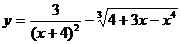 ;
;
в)  ; г)
; г) 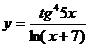 .
.
39. а) 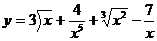 ; б)
; б) 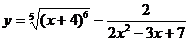 ;
;
в) 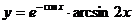 ; г)
; г) 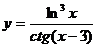 .
.
40. а) 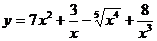 ; б)
; б) 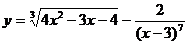 ;
;
в) 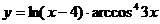 ; г)
; г) 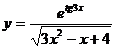 .
.
41-50.Найти 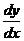 и
и 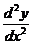 для заданных функций и вычислить их значения в данной точке х0.
для заданных функций и вычислить их значения в данной точке х0.
41. 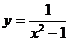 , х0 = 0.
, х0 = 0.
42.у = sin2x , x0 = p/2.
43. y = ln(2 + x2), x0 = 0.
44. y = x4 lnx, x0 = 1.
45. y = exsin2x, x0 = 0.
46. y = x sinx, x0 = p/2.
47. y = (x+1) ln(x+1), x0 = -1/2.
48. y = ln3x, x0 = 1.
49. y = e-x cosx, x0 = 0.
50. y = x2 lnx, x0 = 1/3.
51-60.Найти дифференциалы первого и второго порядка для заданных функций и вычислить их значения в заданной точке х0.
51. 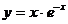 , х0 = 0.
, х0 = 0.
52. 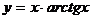 , х0 =1.
, х0 =1.
53. 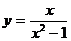 , х0 = 0.
, х0 = 0.
54. 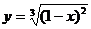 , х0 = 2.
, х0 = 2.
55. 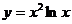 , х0 =1.
, х0 =1.
56. 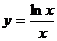 , х0 = 1.
, х0 = 1.
57. 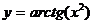 , х0 = -1.
, х0 = -1.
58. 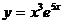 , х0 = 0.
, х0 = 0.
59. 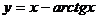 , х0 = -1.
, х0 = -1.
60. 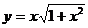 , х0 = 0.
, х0 = 0.
61-70.С помощью дифференциала вычислить приближенное значение данной величины.
61. 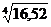 .62.tg 460.
.62.tg 460.
63. 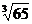 .64.arctg 1,05.
.64.arctg 1,05.
65. 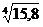 . 66.cos 590.
. 66.cos 590.
67.e2,01 . 68.ctg 440.
69. lg 11. 70.sin 1510.
71.Проверитьсправедливость теоремы Ролля для функции y = 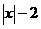 на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
72. Найти точку, в которой касательная к кривой y = x2 – 4x параллельно хорде, соединяющей точки А (1, –3) и В (5,5). Сделать поясняющий рисунок.
73. Проверить справедливость теоремы Лагранжа для функции y=еx на данном отрезке [0,1]. Найти соответствующее значение с (если оно существует).
74.Дана функция y = 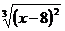 . Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
. Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
75. Проверитьсправедливость теоремы Ролля для функции y = –x2 + 4x –3 на данном отрезке [0,4]. Найти соответствующее значение с (если оно существует).
76. Найти точку, в которой касательная к кривой y = ln x параллельно хорде, соединяющей точки А (1, 0) и В (е,1). Сделать поясняющий рисунок.
77. Проверить справедливость теоремы Лагранжа для функции y = 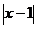 на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
78. Проверитьсправедливость теоремы Ролля для функции y = 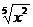 на данном отрезке [1,1]. Найти соответствующее значение с (если оно существует).
на данном отрезке [1,1]. Найти соответствующее значение с (если оно существует).
79. Проверить справедливость теоремы Лагранжа для функции y=  на данном отрезке [
на данном отрезке [ 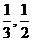 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
80. Проверитьсправедливость теоремы Ролля для функции y = cos x на данном отрезке [ 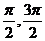 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
81-90.Найти пределы, используя правило Лопиталя.
81. 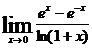 . 86.
. 86. 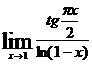 .
.
82. 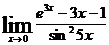 . 87.
. 87. 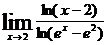 .
.
83. 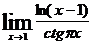 . 88.
. 88. 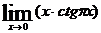 .
.
84. 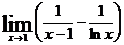 . 89.
. 89. 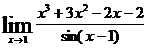 .
.
85. 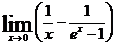 . 90.
. 90. 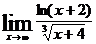
91.-100.Исследовать методами дифференциального исчисления функции 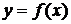 и, используя результаты исследования, построить их графики.
и, используя результаты исследования, построить их графики.
91. а) 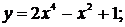 б)
б) 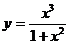
92. а) 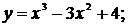 б)
б) 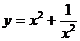
93. а) 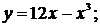 б)
б) 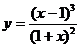
94. а) 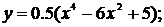 б)
б) 
95. а) 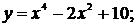 б)
б) 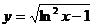
96. а) 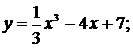 б)
б) 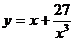
97. а) 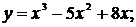 б)
б) 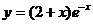
98. а) 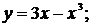 б)
б) 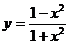
99. а) 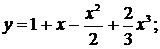 б)
б) 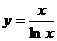
100. а) 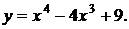 б)
б) 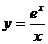
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.
