Полагаем, что в произвольном подмножестве натуральных чисел всегда есть наименьшее.
Делимость целых чисел.
Полагаем, что в произвольном подмножестве натуральных чисел всегда есть наименьшее.
Определение. Пусть a, bÎZ. Если существует qÎZ, что a = bq, то b делит a, или a делится на b, обозначаем b|a.
Простейшие свойства делимости:
1) Если a|b, b|c Þ a|c. Если a делит b и b делит c, то a делит c.
2) Если a,b,с  и с не равно 0, то a делит b тогда и только тогда, когда ac делит bc, т. е. a|b; c¹0 Û ac|bc, a, b, cÎZ.
и с не равно 0, то a делит b тогда и только тогда, когда ac делит bc, т. е. a|b; c¹0 Û ac|bc, a, b, cÎZ.
3) d|ai; i=1,…,n,
x1,…,xnÎZ Þ d|a1 x1 +…+an xn.
4) a|b; b|a Þ a =±b.
Доказательство всех свойств однообразно: используется только определение делимости. Докажем 4) :
a = bq и b = aq1 Þ a = aqq1 Þ a(qq1 – 1) = 0 Þ qq1 = 1, т. к. a¹0 Þ q = ±1.
Теорема (о делении с остатком).
Для любых a, bÎZ; b ¹ 0 существует единственная пара q, rÎZ такая, что a = bq+r, 0£ r<|b|.
Доказательство: Рассмотрим множество M = {a – bq, qÎZ}. Очевидно, что M∩{N, 0}¹Ø.
В любом таком множестве $ наименьшее r. Очевидно, что |b|>r ≥0.
Докажем единственность.
Пусть ещё a = bq1 + r1. Тогда вычитанием из первого второе получим
0 = b(q – q1) + r – r1. Отсюда следует, что r – r1 кратно b, но |r – r1|<|b|.
Следовательно, r – r1 = 0, а поэтому и q – q1 = 0.
Упражнение.Доказать теорему о делении с остатком геометрически (использовать геометрическую интерпретацию чисел).
Следствие из теоремы.
b делит a тогда и только тогда, когда r = 0 (b|a Û r = 0);
r называют остатком, а q – частным.
Построение комплексных чисел.
Уравнение x2+1=0 не имеет решения в области действительных чисел. Построение комплексных чисел попутно решает задачу о расширении множества действительных чисел до такого множества, чтобы уравнение x2+1=0 имело решение.
В качестве исходного материала для построения комплексных чисел возьмём множество точек плоскости. Будем их обозначать z1, z2,…, zn. Если на плоскости выбрана Декартова система координат, то между точками на плоскости и множеством пар чисел (a, b), где a и bÎR, можно установить взаимно однозначное соответствие, т.е.
z  (a, b), где
(a, b), где  – равно по определению.
– равно по определению.
Введём операции сложения и умножения точек плоскости.
Определение 1.Под суммой точек z1=(a, b) и z2=(c, d) будем понимать точку z = z1+z2  (a+c, b+d).
(a+c, b+d).
Определение 2.Под произведением точек z1=(a, b) и z2=(c, d) будем понимать точку z = z1z2  (ac–bd, ad+bc)
(ac–bd, ad+bc)
Теорема 1.
1) z1+z2=z2+z1 — коммутативность сложения;
2) (z1+z2)+z3= z1+(z2+z3) — ассоциативность сложения;
3) z1z2= z2z1 — коммутативность умножения;
4) (z1z2)z3= z1(z2z3) — ассоциативность умножения;
5) (z1+z2)z3 = z1z3+z2z3 — дистрибутивность умножения относительно сложения.
Для любых z1, z2, z3.
Доказательство утверждений 1) – 5) сводится к подсчёту правой и левой частей и проверке их равенства. Докажем, например, 3) :
z1z2 = (ac–bd, ad+bc) = (ca–db, cb+da) = z2z1 Þ z1z2= z2z1.
Введённые операции сложения и умножения обладают теми же свойствами, что и числа.
Определение 3.Под разностью точек z1=(a, b) и z2=(c, d) будем понимать точку z = (x, y) такую, что z2+ z = z1, т.е.
z2+z = z1 Û  Þ
Þ 
z1–z2 = (a – c, b – d).
Определение 4.Пусть z1 = (a, b), z2 = (c, d), z2 ¹ (0, 0).
Частным двух точек z1 и z2 называют точку z = (x, y) такую, что z2z = z1, т.е.
 Þ
Þ 
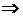
x =  ; y =
; y =  .
.
Точка с координатами (0, 0) играет роль нуля. Роль единицы играет точка с координатами (1, 0). Противоположной точке z1 = (a, b) будет точка z2 = (–a, –b).
Упражнение. Найти обратную точку для точки z2 = (c, d)≠(0,0).
Множество точек плоскости с так введёнными операциями сложения, умножения, вычитания и деления называют множеством комплексных чисел и обозначают C.
Точки с координатами (a, 0) на оси Ox и
(a, 0)+(b, 0) = (a+b, 0), (a, 0)(b, 0) = (ab, 0).
По своим свойствам множество таких точек ничем не отличаются от R, поэтому будем отождествлять (a, 0) и a. После этого отождествления множество C содержит R (C É R).
В множестве C имеет решение уравнение x2+1=0.
Это точка с координатами (0, 1): (0, 1) (0, 1) = (–1, 0).
Точка (0, 1) — обозначается i и называется мнимой единицей. Очевидно, что
(a, b) = (a, 0)+(0, b) = a+(b, 0)(0, 1) = a+bi, где a+bi — алгебраическая форма комплексного числа.
Замечание. Введенные ранее операции над комплексными числами приспособлены к алгебраической форме записи комплексного числа. Например, для умножения двух чисел имеем:
(a+bi)(c+di) = ac+adi+cbi+bdi2=(ac–bd)+i(ad+bc).
Пусть z = a+bi, тогда:
a = Re z — действительная часть комплексного числа,
b = Im z — мнимая часть комплексного числа.
Множество точек плоскости может служить геометрическим изображением комплексных чисел.
Определение 5.Два комплексных числа равны, если равны их мнимые и действительные части (следует из геометрической интерпретации комплексных чисел).
Два комплексных числа называют сопряжёнными, если их действительные части равны, а мнимые — противоположны (сопряжённое к z обозначаем через  ).
).
Упражнение 1.Сумма и произведение двух комплексных чисел z и  (сопряжённых) — действительное число.
(сопряжённых) — действительное число.
Теорема 2.
Справедливы следующие соотношения:
1)  =
=  +
+  ;
;
2)  =
=  –
–  ;
;
3)  =
= 
 ;
;
4)  =
=  .
.
Доказательство.
Доказательство 1) – 4) однообразно и сводится к подсчёту левой и правой частей и их сравнению. Например: z1=a+bi, z2=c+di. Докажем
1)  =
=  +
+  . По определению
. По определению
 = a-bi ;
= a-bi ;  =c-di и
=c-di и
 = (a+c)–(bi+di),
= (a+c)–(bi+di),
 +
+  = (a–bi)+(c–di) = (a+c)–(bi+di).
= (a–bi)+(c–di) = (a+c)–(bi+di).
Значит  =
=  +
+  .
.
§3. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА
КОМПЛЕКСНОГО ЧИСЛА.
Пусть z = a+bi , полагаем r 
 =|z|, r — модуль комплексного числа z.
=|z|, r — модуль комплексного числа z.
a+bi = 
 , положим
, положим
 = cos
= cos  и
и  = sin
= sin  .
.
Пусть z¹0, тогда угол j определен однозначно с точностью до 2pk. Если 0£j£2p, то он определен однозначно. Угол j называют аргументом комплексного числа z, r и j — полярные координаты точки.
Из тригонометрии мы знаем как искать j, если известно a и b.
Если r=0, то j может быть любой, то есть аргумент нуля не определён; r¹0, то аргумент определен с точностью до 2πk.
z = r(cosj+i sinj) (1)
Назовем выражение (1) тригонометрической формой комплексного числа.
Если два комплексных числа равны, то их модули равны, а их аргументы, вообще говоря, отличаются на 2pk.
Теорема 1.
Пусть z1 = r1 (cosj1+i sinj1), z2 = r2 (cosj2+i sinj2). Тогда:
1) z1z2 = r1r2(cos(j1+j2)+i sin(j1+j2))
 |
(модуль произведения комплексных чисел равен произведению модулей, а аргумент – сумме аргументов);
2)
(модуль частного комплексных чисел равен частному модулей, а аргумент – разности аргументов).
Доказательство:
Докажем 1).
z1z2 = r1r2(cosj1cosj2– sinj1sinj2+i(sinj1cosj2+cosj1sinj2)) = =r1r2cos(j1+j2)+i sin(j1+j2)).
Аналогично с частным.
Следствие 1.
Пусть z = r (cosj+i sinj), тогда z  =
=  (cos(–j)+i sin(–j)).
(cos(–j)+i sin(–j)).
Доказательство:
z  =
=  =
=  =
=  =
=  (cos(–j)+i sin(–j)).
(cos(–j)+i sin(–j)).
Следствие 2(формула Муавра).
Пусть z = r (cosj+i sinj). Тогда zn = rn(cos(nj)+i sin(nj)) для любого nÎZ.
Доказательство:
Если n — натуральное, то формула Муавра следует из правила умножения комплексных чисел в тригонометрической форме.
Если n — отрицательное, то можно представить zn = (z -1)-n и применить следствие (1) и доказанную формулу Муавра для nÎN.
ИЗВЛЕЧЕНИЕ КОРНЯ
ИЗ КОМПЛЕКСНОГО ЧИСЛА.
Пусть z = a+bi.
Надо извлечь корень из z.
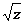 — ?
— ?
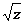 обозначим через z1, то z
обозначим через z1, то z 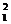 = z.
= z.
Пусть z1 = x+iy, тогда
(x2–y2)+2xyi = a+bi,
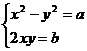
Решив эту систему, мы найдем подходящие значения z1.
Если так действовать и для извлечения корней более высокой степени, то придётся уметь решать уравнения соответствующих степеней.
Для извлечения корня из комплексного числа хорошо приспособлена тригонометрическая форма комплексного числа.
Пусть z = r(cosj+i sinj), надо найти 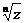 = z1, положим
= z1, положим
z1=ρ (cosy+i siny), z 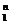 ==ρn(cos(ny)+i sin(ny), r = ρn Þ ρ =
==ρn(cos(ny)+i sin(ny), r = ρn Þ ρ = 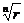 , j = ny+2pk
, j = ny+2pk 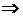 y =
y = 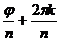 .
.
Получим
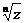 =
= 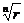 (cos
(cos 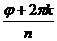 +i sin
+i sin 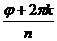 ) (1),
) (1),
где k — любое целое число, то есть корень n–той степени из произвольного комплексного числа z всегда существует и его можно посчитать по формуле (1), причем формула (1) даёт все корни, если k пробегает множество целых чисел (достаточно ограничиться k = 0,…, n–1 )
Если возьмем k – любое, то мы можем разделить его с остатком на n:
k = nq+s ; 0£s£n–1
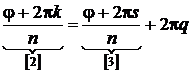 .
.
Углы [2] и [3] отличаются на кратное 2p, и поэтому косинусы и синусы от них совпадают, следовательно формула (1) при угле [2] и при угле [3] даёт одинаковое значение.
Если брать k от 0 до n–1 , то мы получим все значения. Нетрудно заметить, что все эти значения разные (смотри геометрическую интерпретацию).
Теорема 4.
Извлечение корня степени n из комплексного числа всегда возможно, и даёт n различных значений, получающихся по формуле (1).
Теорема нами доказана ранее.
Замечание(геометрическая интерпретация).
Все значения 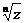 расположены на окружности радиуса
расположены на окружности радиуса 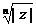 с центром в начале координат и делят окружность на n равных частей:
с центром в начале координат и делят окружность на n равных частей:

§5. КОРНИ ИЗ ЕДИНИЦЫ.
1 = cos0+i sin0 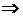
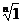 = cos
= cos 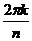 +i sin
+i sin 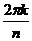 ,
, 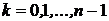 .
.
Корни расположены на окружности единичного радиуса и делят эту окружность на n равных частей.
Теорема 1.
Все значения корня n–той степени из комплексного числа z можно получить умножением одного из них на все корни из 1.
Доказательство:
Возьмём a = 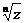 =
= 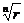 (cos
(cos 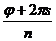 +i sin
+i sin 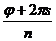 ), где s–фиксированное число.
), где s–фиксированное число.
e1, e2,…, en – так обозначим все корни 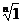 .
.
Домножим каждый из корней e1,…, en на a. Они разные, все являются корнями n–той степени из z, ибо (aei)n = z и их 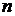 штук.
штук.
Теорема доказана.
Теорема 2.
Произведение двух корней n–той степени из единицы есть корень степени n из единицы.
Следствие.
Степень корня n–той степени из единицы есть корень степени n из единицы.
Все ли корни из 1 равноправны?
n=4 ; 1, –1, i, –i — корни из единицы.
i; –i — первообразные корни; если i возводить в степени 0, 1, 2, 3, то получим все корни.
Определение 1.
Корень n–той степени из 1 называется первообразным, если он не даёт единицу в степени меньше, чем n.
ЧИСЛОВОЕ ПОЛЕ.
В множествах Q Ì R Ì C возможны четыре операции +, –,× , :.
Определение 1. Подмножество K Ì C множества комплексных чисел C, состоящее более, чем из одного элемента, называют числовым полем, если выполняются следующие условия:
1) " a, bÎK Þ a+bÎK , то есть в множестве K всегда возможно сложение;
2) " aÎK Þ –aÎK ;
3) " a, bÎK Þ abÎK , то есть задано умножение в K (K замкнуто относительно умножения);
4) " a ¹ 0 ; a -1ÎK.
Из 2) с учётом 1) получаем, что в K всегда возможно вычитание.
Из 4) с учётом 3) получаем, что в K всегда возможно деление на число не равное 0.
Q — поле рациональных чисел;
R — поле вещественных чисел;
C — поле комплексных чисел.
Умножение матриц.
Мы никак не мотивировали операцию сложения матриц, но едва ли это вызвало недоумение в силу своей естественности. Операция умножения матриц уже не обладает этим качеством.
Пусть A = (aij)m x n , B = (bij)n x p. Под произведением АВ понимают

матрицу С с элементами cij = .
АВ := С= (сij)m x p.


Например, А = и В = .

Тогда AВ =
5=1 · 0 + 2 · 1 + 3 · 1
6=1 · 1 + 2 · 1 + 3 · 1
7= 1 · 4 + 2 · 0 + 3 · 1 и т.д.
Берется i-тая строка матрицы А и j-тый столбец матрицы В, перемножаются покомпонентно и результаты складываются. Это есть элемент матрицы С на позиции i,j.
Свойство. Произведение матриц не коммутативно, т.е. АВ ¹ ВА, в том числе и квадратных.
Пример (доказывающий свойство):



=



=
Замечание 1. Запись A = (aij)m x n обозначает, что матрица А имеет размеры
m x n.
Замечание 2. В двойной сумме результат суммирования не зависит от порядка суммирования, т.е.
 , ибо левая часть равенства и правая часть есть сумма элементов матрицы
, ибо левая часть равенства и правая часть есть сумма элементов матрицы  .
.
Транспонирование матриц.
Определение 1. Пусть A = (aij)m x n . Транспонирование матрицы — это такое ее преобразование, при котором строка с номером i записывается в столбец с тем же номером.
Обозначение: Аt , Аtr , А'.
Пример:
 , то
, то  .
.
Теорема 5.Имеют место следующие равенства:
1. (Аt)t = A.
2. (αA + βB)t = αAt + βBt.
3. (AB)t = ВtАt .
Причем, А и В — матрицы подходящих размеров, α и β — любые числа.
¢ 1. А = (аij)m x n
(A)t = (аji)n x m 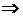 (Аt)t = A.
(Аt)t = A.
2. Доказать самостоятельно.
3. Пусть имеем А = (аij)m x n и B = (bij)n x s . Тогда At = (  ij)n x m , Bt = =(
ij)n x m , Bt = =(  ij)s x n, AB = (cij)m x s, BtАt = (dij)s x m , (AB)t = (
ij)s x n, AB = (cij)m x s, BtАt = (dij)s x m , (AB)t = (  ij)s x m.
ij)s x m.
Матрица ВtAt и (AB)t одинаковых размеров, и чтобы доказать, что ВtAt = (AB)t , надо показать, что на одинаковых местах стоят одинаковые элементы.
 .
.
Мы получили, что на позиции ij у матрицы ВtAt и матрицы (AB)t стоит один и тот же элемент. £
Определение 2. Матрица А называется симметрической, если Аt = А, и кососимметрической, если Аt = -А.

Пример. Симметрическая матрица:

кососимметрическая матрица:
Упражнение. Будет ли произведение симметрических (кососимметрических) матриц симметрической (кососимметрической) матрицей? Если будет, доказать. Если не будет, привести пример.
Перестановки.
Пусть X — непустое множество элементов произвольной природы, так как природа элементов для нас несущественна, то в случае конечного множества считаем X =  .
.
Определение 1. Любое упорядоченное расположение элементов множества X называется перестановкой множества X.
Пример:
Если X =  , то (2,5,3,4,1) - перестановка множества X.
, то (2,5,3,4,1) - перестановка множества X.
Перестановку элементов множества X обозначают  , причем среди
, причем среди  (i = 1,2,…, n)
(i = 1,2,…, n)  нет равных.
нет равных.
Определение 2. Две перестановки множества X называются равными, если у них на одинаковых местах стоят одинаковые элементы.
Теорема 1.Число различных перестановок множества из n элементов равно n!
◄ Докажем эту теорему индукцией по числу  . При
. При  1 имеется одна перестановка, т.е. 1!.
1 имеется одна перестановка, т.е. 1!.
Пусть  >1 и число различных перестановок, которые можно составить из заданных (
>1 и число различных перестановок, которые можно составить из заданных (  ) элементов, равно
) элементов, равно  . Всякая перестановка данных элементов с фиксированным первым числом а имеет вид:
. Всякая перестановка данных элементов с фиксированным первым числом а имеет вид:
 ,
,
где  произвольная перестановка оставшихся (
произвольная перестановка оставшихся (  ) элементов. По индуктивному предположению число таких перестановок равно
) элементов. По индуктивному предположению число таких перестановок равно  .В качестве а, можно взять любой из данных
.В качестве а, можно взять любой из данных  элементов, поэтому число различных перестановок заданных
элементов, поэтому число различных перестановок заданных  элементов равно сумме n слагаемых, каждое из которых есть
элементов равно сумме n слагаемых, каждое из которых есть  , т.е. n!►
, т.е. n!►
Определение 3. Будем говорить, что в перестановке чисел  два числа
два числа  образуют инверсию если
образуют инверсию если  >
>  , но i < j. В противном случае
, но i < j. В противном случае  образуют порядок.
образуют порядок.
Пример:
В перестановке (1 3 4 2) инверсии: 4,2 ; 3,2 , а остальные пары образуют порядок.
Определение 4. Количество пар чисел, образующих инверсию в перестановке, называют числом инверсий данной перестановки. Отображение  X
X  X будем называть преобразованием множества X.
X будем называть преобразованием множества X.
Пусть множество X состоит не менее чем из двух элементов  X.
X.
Определение 5. Преобразование множества Х называют транспозицией элементов  и
и  , если
, если  ,
,  ,
, 

 .Такое преобразование обозначают
.Такое преобразование обозначают  .
.
Определение 6. Перестановку называют четной, если число инверсий в ней четно, и нечетной в противном случае.
Теорема 2.Однократное применение транспозиции к перестановке изменяет ее характер четности на противоположный.
◄ Пусть имеется перестановка 
 . Применим к ней транспозицию
. Применим к ней транспозицию  , получим
, получим 
 . Рассмотрим несколько случаев:
. Рассмотрим несколько случаев:
1. Пусть  и
и  стоят рядом. Если
стоят рядом. Если  и
и  в
в  образуют инверсию, то
образуют инверсию, то  образуют порядок. Поэтому характер четности изменяется на противоположный, ибо число инверсий изменяется на единицу.
образуют порядок. Поэтому характер четности изменяется на противоположный, ибо число инверсий изменяется на единицу.
2. Пусть  и
и  не стоят рядом
не стоят рядом  . От
. От  к
к  можно перейти следующим способом:
можно перейти следующим способом:  менять с рядом стоящим элементом дойти до
менять с рядом стоящим элементом дойти до  и
и  перегнать на место
перегнать на место  . Всего нам придется применить S+1+S=2S+1 транспозиций соседних чисел, где
. Всего нам придется применить S+1+S=2S+1 транспозиций соседних чисел, где  число элементов между
число элементов между  и
и  , поэтому характер четности перестановок
, поэтому характер четности перестановок  и
и  различны.►
различны.►
Следствие.При  2 число четных перестановок равно числу нечетных перестановок и равно
2 число четных перестановок равно числу нечетных перестановок и равно  .
.
◄ Пусть число четных перестановок равно S, нечетных — T. Если к каждой четной перестановке мы применим транспозицию двух элементов, мы превратим их в нечетные S  , аналогично наоборот T
, аналогично наоборот T 
 T=S
T=S
 =S+T =2S
=S+T =2S
S=T=  .►
.►
Теорема 3.Пусть даны две различные перестановки одних и тех же чисел, тогда существует последовательность транспозиций переводящих первую перестановку во вторую.
◄ Пусть




есть произвольные перестановки из n чисел. Если  , то применив к перестановке
, то применив к перестановке  транспозицию
транспозицию  получим перестановку n чисел вида
получим перестановку n чисел вида


Если  , то к перестановке
, то к перестановке  применим транспозицию
применим транспозицию  .В результате получим перестановку
.В результате получим перестановку  . Продолжаем этот процесс получаем требуемое.►
. Продолжаем этот процесс получаем требуемое.►
Замечание.В доказательстве теоремы содержится алгоритм нахождения последовательности транспозиций, переводящих одну перестановку в другую.
Пример:
(1, 2, 3, 4) 
(3, 1, 4 ,2) 
(1,2,3,4)  (3,2,1,4)
(3,2,1,4)  (3,1,2,4)
(3,1,2,4)  (3,1,4,2).
(3,1,4,2).
(6) (7)
Такая последовательность транспозиций не однозначна (это может быть не самый короткий путь перехода от одной перестановки к другой).
Подстановки.
Пусть  X
X  X , при этом если
X , при этом если  — биективно, то часто
— биективно, то часто  называют подстановкой. Мы ограничимся случаем, когда число элементов конечно, и равно n .
называют подстановкой. Мы ограничимся случаем, когда число элементов конечно, и равно n .
X =  , тогда отображение можно записать в виде таблицы:
, тогда отображение можно записать в виде таблицы:


Если  подстановка, тогда
подстановка, тогда  — перестановка. Запись отображения
— перестановка. Запись отображения  в виде таблице (1) позволяет хорошо перемножать отображения.
в виде таблице (1) позволяет хорошо перемножать отображения.
Пример.


Теорема 1.Всякая подстановка конечного множества, содержащая не менее двух элементов, может быть представлена в виде произведения транспозиций.
◄ Пусть имеем 
 .Согласно теореме 3 предыдущего параграфа, существует последовательность транспозиций переводящая первую перестановку во вторую, пусть это будет следующая последовательность транспозиций
.Согласно теореме 3 предыдущего параграфа, существует последовательность транспозиций переводящая первую перестановку во вторую, пусть это будет следующая последовательность транспозиций  . Тогда очевидно, что
. Тогда очевидно, что  , ибо отображения действуют на одном и том же множестве и результат их действия одинаков. ►
, ибо отображения действуют на одном и том же множестве и результат их действия одинаков. ►
Замечание. Разложение подстановки в произведение транспозиций, вообще говоря, неоднозначно.
Теорема 2.Характер четности числа сомножителей во всех разложениях подстановки в произведение транспозиций один и тот же.
◄ Пусть подстановка вида (1) разлагается в произведение k транспозиций. Это значит, что существует последовательность k транспозиций, переводящая перестановку  (2) в перестановку
(2) в перестановку  (3). Однократное применение транспозиции меняет характер четности перестановки, поэтому k — четное число тогда и только тогда, когда перестановки(2) и (3) одного характера четности. Это и доказывает теорему.►
(3). Однократное применение транспозиции меняет характер четности перестановки, поэтому k — четное число тогда и только тогда, когда перестановки(2) и (3) одного характера четности. Это и доказывает теорему.►
Определение 1. Подстановка называется четной, если она разлагается в произведение четного числа транспозиций, и нечетная в противном случае.
Упражнение. Число четных подстановок равно числу нечетных и равно  .
.
Определители и их свойства.
Пусть А — некоторая матрица размеров n x n над полем Р.

A =
Возьмем из каждой строки и каждого столбца матрицы по одному элементу  . Тогда (i1 ..........in ) (1) будет некоторой перестановкой чисел 1,2, … , n. Возьмем произведение этих элементов и умножим на (-1) t , где t — число инверсий в перестановке (1). Получим (-1) t
. Тогда (i1 ..........in ) (1) будет некоторой перестановкой чисел 1,2, … , n. Возьмем произведение этих элементов и умножим на (-1) t , где t — число инверсий в перестановке (1). Получим (-1) t  (2). Это произведение (2) принято называть членом определителя матрицы А.
(2). Это произведение (2) принято называть членом определителя матрицы А.
Определение. Определителем (детерминантом) матрицы А назовем сумму всех членов определителя матрицы А.
Определитель матрицы А обозначается одним из символов: | A | , det A .
Замечание. Количество членов определителя матрицы А равно n!
Примеры:
1) n=1; A = (a11) . Определитель матрицы равен a11.

2) n=2; A = , тогда det A = а11а22 – а12а21.
 3) n=3; A = , тогда det A = a11a22a33 + a12a23a31 + a13a21a32 –
3) n=3; A = , тогда det A = a11a22a33 + a12a23a31 + a13a21a32 –
– a13a22a31 – a12a21a33 – a11a23a32.
Если  , считать определитель по определению становится уже громоздким. Для того, чтобы считать определитель, нужно использовать его свойства.
, считать определитель по определению становится уже громоздким. Для того, чтобы считать определитель, нужно использовать его свойства.
Свойства определителей.
1) Определитель матрицы не изменяется при ее транспонировании, т.е.
det A = det At.
2) Если у матрицы поменять местами две строки, то ее определитель изменит знак на противоположный.
3) Определитель матрицы с нулевой строкой равен 0.
4) Определитель матрицы, содержащий две равные строки, равен 0.
5) Постоянный множитель всех элементов какой-нибудь строки определителя можно выносить за знак определителя.
6) Определитель матрицы, содержащей две пропорциональные строки,
равен 0.


 7)
7)
d = = + ,
|| ||
d1 d2
где aik=bik+cik , где к = 1, ... , n.
Определитель матрицы d, у которой i-тая строка представлена в виде aik=bik+cik , где к = 1, … , n, равен сумме определителей d1 и d2 , которые отличны от d i - той строкой, а именно, у d1 i–тая строка bik ,  у d2 - cik,
у d2 - cik,  .
.
8) Если в определителе к какой–нибудь строке прибавить другую строку, умноженную на произвольное число, то определитель при этом не изменится.
¢ Доказательство всех этих свойств основано на определении определителя и несложных наблюдениях.
Докажем, например, свойство 1.
Пусть А = (aij), At = (bij) — транспонированная к А матрица, т.е.
bij = aji. (3)
Требуется доказать, что | A | = | At |.
Рассмотрим произвольный член определителя | At | : (-1)t  (4),
(4),
где t — число инверсий в перестановке j1, j2, …, jn (5). Учитывая (3), перепишем (4) в виде (-1)t  = (-1)t
= (-1)t  (6). Так как (5) — перестановка из n чисел, то правую часть (6) можно переписать следующим образом: (-1)t
(6). Так как (5) — перестановка из n чисел, то правую часть (6) можно переписать следующим образом: (-1)t  = (-1)t
= (-1)t  (7). Это равносильно тому, что подстановка
(7). Это равносильно тому, что подстановка  (8) записывается в виде
(8) записывается в виде  (9).
(9).
Из (6) и (7) получаем (-1)t  = (-1)t
= (-1)t  (10).
(10).
Правая часть равенства (10) есть с точностью до знака член определителя | A |. Покажем, что перестановка l1, l2, …, ln (11) имеет тот же характер четности, что и перестановка (5).
Действительно, перестановка (11) имеет ту же четность, что и подстановка (9), равная подстановке (8). Четность подстановки (8) совпадает с четностью обратной к ней подстановки  (12). Наконец, подстановка (12) имеет ту же четность, что и перестановка (5). Итак, если k — число инверсий в перестановке (11), то с учетом (10) имеем (-1)t
(12). Наконец, подстановка (12) имеет ту же четность, что и перестановка (5). Итак, если k — число инверсий в перестановке (11), то с учетом (10) имеем (-1)t  = (-1)k
= (-1)k  , т.е. член определителя |At|, соответствующий перестановке (5), равен члену определителя |A|, соответствующий перестановке (11). Отсюда и следует равенство определителей |A| и |At|.
, т.е. член определителя |At|, соответствующий перестановке (5), равен члену определителя |A|, соответствующий перестановке (11). Отсюда и следует равенство определителей |A| и |At|.
Докажем теперь свойство 7.
Если (-1)t  есть произвольный член определителя (напомним, что t — число инверсий в перестановке j1,..., ji, ..., jn), то
есть произвольный член определителя (напомним, что t — число инверсий в перестановке j1,..., ji, ..., jn), то
d = å(-1) t  = å(-1) t
= å(-1) t  =
=
= å(-1) t  + å(-1) t
+ å(-1) t  = d1 + d2 . £
= d1 + d2 . £
Замечание. Так как при транспонировании матрицы столбцы становятся строками, то из свойства 1 следует, что все утверждения, доказанные нами для строк определителя, верны и для его столбцов.


Пример 1. det = det = 1 · 1 · 2 · 7 = 14.

Пример 2. det = а11… аnn.
Обратная матрица.
Пусть A = (aij)n x n квадратная матр
