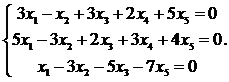Структура общего решения неоднородной линейной системы
Рассмотрим неоднородную линейную систему (1). Такая система будет совместной, если ранг матрицы системы (7) равен рангу расширенной матрицы, то есть матрицы системы, к которой добавлен столбец свободных членов:
.
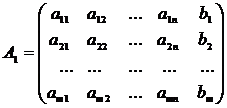Ее общее решение можно получить, выражая базисные неизвестные через свободные, то есть решая систему относительно базисных неизвестных (такая система всегда определена, что следует из правила Крамера).
Пример 17.
Найти общее решение и одно из частных решений линейной системы
.
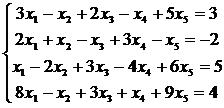Решение.
Найдем r(A) и r(A1):
~ 
~
~ 
~ 
~
~ 
.
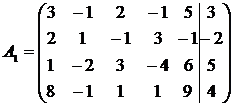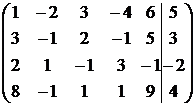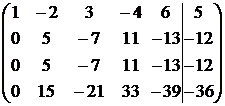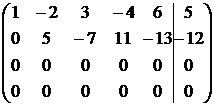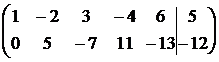Итак, r = r(A) = r(A1) = 2, а число неизвестных п = 5. Следовательно, r < n, и система имеет бесконечно много решений (совместна, но не определена).
Число базисных неизвестных равно r, то есть двум. Выберем в качестве базисных неизвестных х1 и х2, коэффициенты при которых входят в базисный минор преобразованной матрицы А: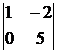 
.
Соответственно х3, х4, х5 – свободные неизвестные.
Запишем систему, равносильную исходной, коэффициентами в которой являются элементы полученной матрицы:
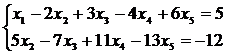
и выразим базисные неизвестные через свободные:
.
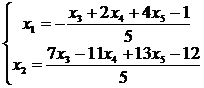Получено общее решение системы. Одно из частных решений можно найти, положив все свободные неизвестные равными нулю: х3 = х4 = х5 = 0. Тогда
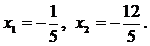
Таким образом, общее решение – ;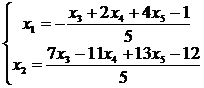
частное решение –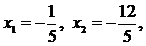 
х3 = х4 = х5 = 0.
Другая возможность получить общее решение неоднородной системы заключается в предварительном нахождении общего решения соответствую-щей однородной системы. При этом искомое общее решение представляет собой сумму общего решения соответствующей однородной системы (6) и частного решения системы (3).
Пример 18.
Найти общее решение неоднородной линейной системы
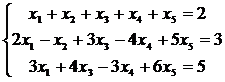
с помощью фундаментальной системы решений соответствующей однородной системы.
Решение.
Убедимся в том, что система совместна:
~ 
~ 
~
~ 
.
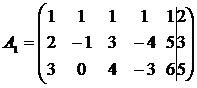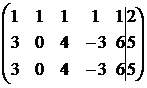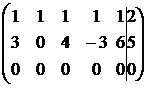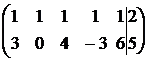Итак, r(A) = r(A1) = 2 – система совместна.
Составим по преобразованной матрице однородную систему:
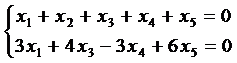
и найдем для нее фундаментальную систему решений:
,
.
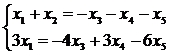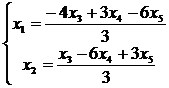Фундаментальная система решений может быть выбрана так:
, 
, 
.
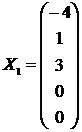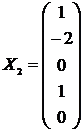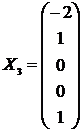Теперь найдем какое-нибудь частное решение неоднородной системы
.
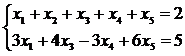Положим х3 = х4 = х5 = 0, тогда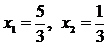 
. Следовательно,
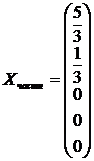, и общее решение системы имеет вид:
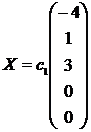
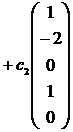
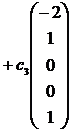
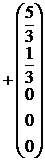, где с1, с2, с3 – произвольные постоянные.
ВАРИАНТЫ ЗАДАНИЙ
Вариант задания выбирается по порядковому номеру в списке группы
Задание №1
Вычислить определитель:
1. 
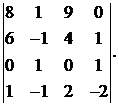
2. 
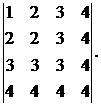
3. 
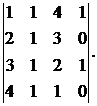
4. 
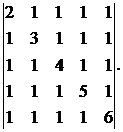
5. 
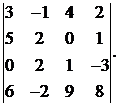
6. 
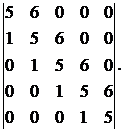
7. 
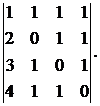
8. 
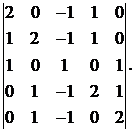
9. 
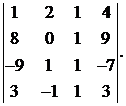
10. 
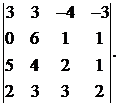
11. 
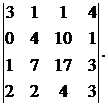
12. 
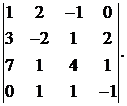
13. 
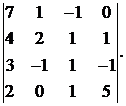
14. 
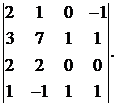
15. 
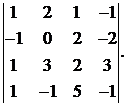
16. 
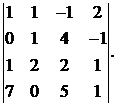
17. 
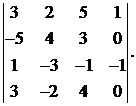
18. 
19. 
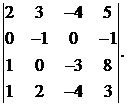
20. 
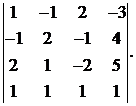
21. 
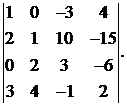
22. 
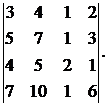
23. 
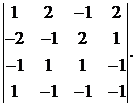
24. 
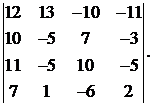
25. 
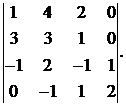
26. 
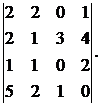
27. 
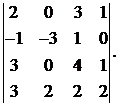
28. 
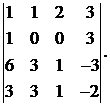
29. 
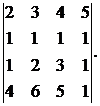
30. 
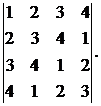
Задание №2
Для матриц A и B вычислить матричный многочлен А2 – ВА + 5А.
1. 
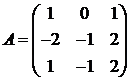
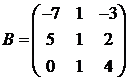
2. 
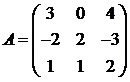
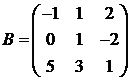
3. 
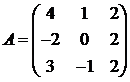
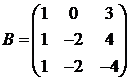
4. 
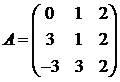
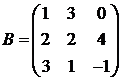
5. 
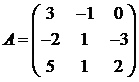
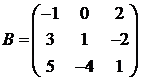
6. 
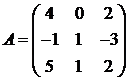
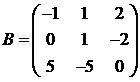
7. 
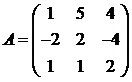
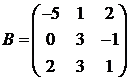
8. 
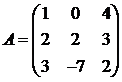
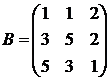
9. 
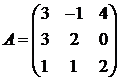
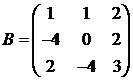
10. 
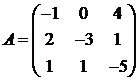
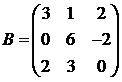
11. 
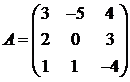
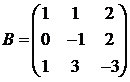
12. 
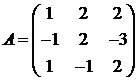
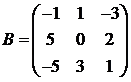
13. 
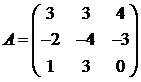
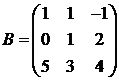
14. 
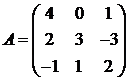
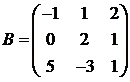
15. 
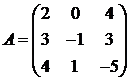
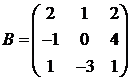
16. 
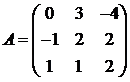
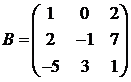
17. 
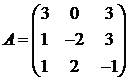
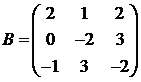
18. 
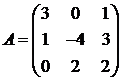
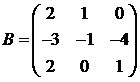
19. 
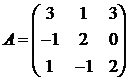
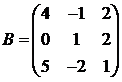
20. 
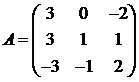
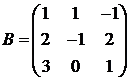
21. 
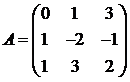
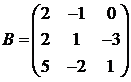
22. 
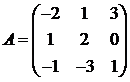
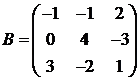
23. 
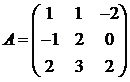
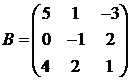
24. 
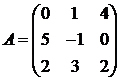
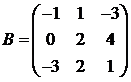
25. 
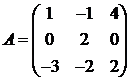
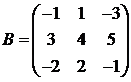
26.
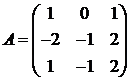
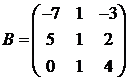
27.
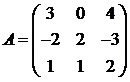
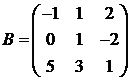
28.
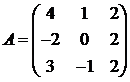
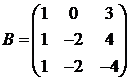
29.
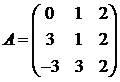
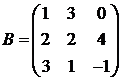
30.
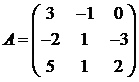
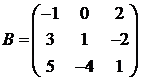
Задание №3
Вычислить обратную матрицу для матрицы:
1. 
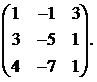
2. 
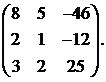
3. 
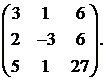
4. 
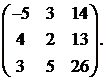
5. 
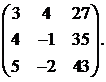
6. 
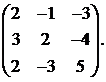
7. 
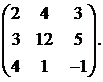
8. 
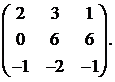
9. 
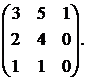
10. 
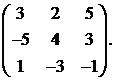
11. 
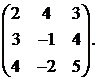
12. 
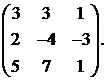
13. 
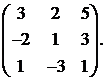
14. 
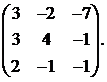
15. 
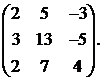
16. 
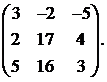
17. 
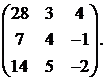
18. 
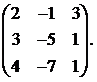
19. 
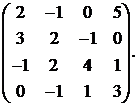
20. 
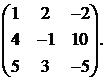
21.
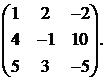
22. 
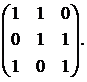
23. 
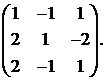
24. 
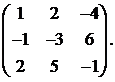
25. 
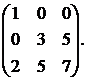
26. 
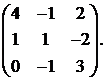
27. 
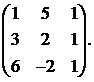
28. 
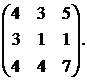
29. 
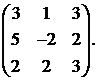
30. 
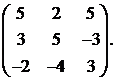
Задание №4
Найти ранг матрицы
1. 
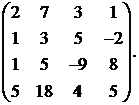
2. 
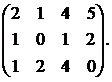
3. 
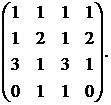
4. 
5. 
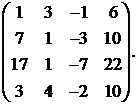
6. 
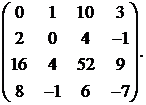
7. 
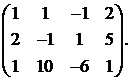
8. 
9. 
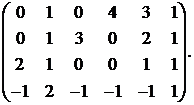
10. 
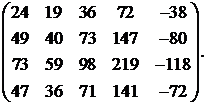
11. 
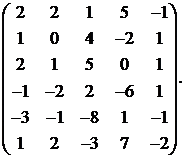
12. 
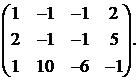
13. 
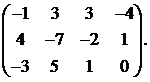
14. 
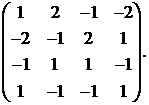
15. 
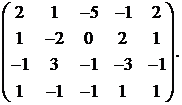
16. 
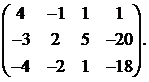
17.
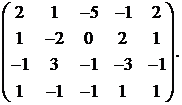
18. 
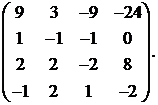
19. 
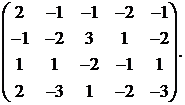
20. 
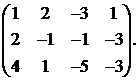
21. 
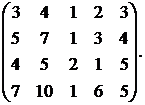
22. 
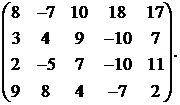
23. 
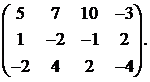
24. 
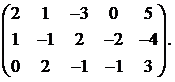
25.
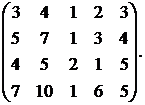
26. 
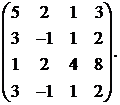
27. 
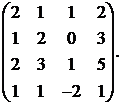
28. 
29.
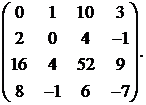
30. 
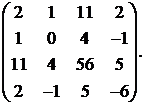
Задание №5
Решить систему уравнений методом Крамера
1. 
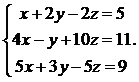
2. 
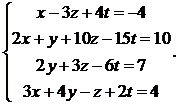
3. 
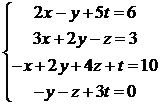
4. 
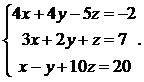
5. 
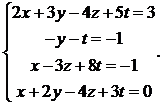
6. 
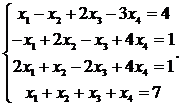
7. 
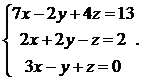
8. 
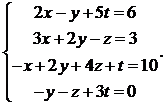
9.
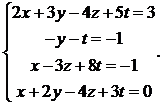
10. 
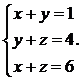
11. 
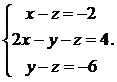
12. 
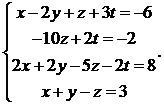
13. 
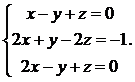
14. 
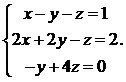
15. 
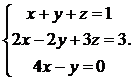
16. 
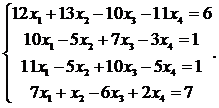
17. 
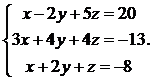
18. 
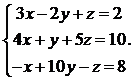
19.
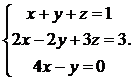
20. 
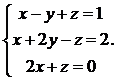
21. 
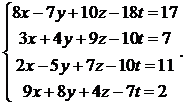
22. 
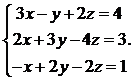
23. 
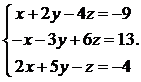
24.
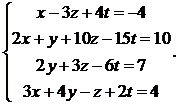
25. 
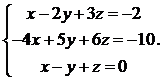
26. 
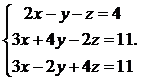
27. 
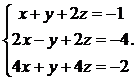
28. 
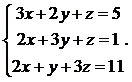
29. 
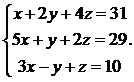
30. 
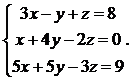
Задание №6
Решить систему уравнений методом Гаусса:
1. 
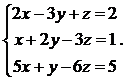
2. 
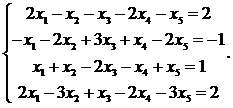
3. 
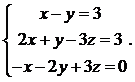
4. 
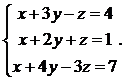
5. 
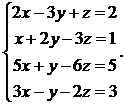
6. 
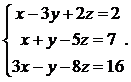
7.
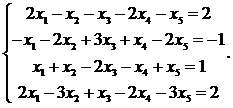
8. 
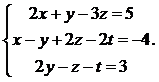
9. 
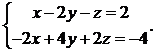
10. 
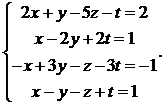
11.
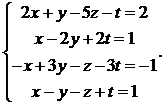
12. 
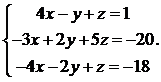
13. 
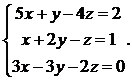
14. 
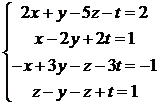
15. 
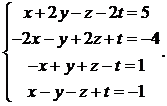
16.
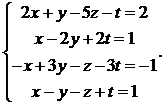
17. 
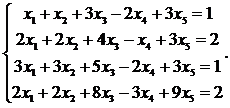
18.
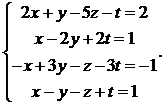
19. 
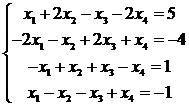
20. 
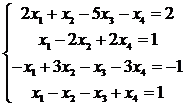
21. 
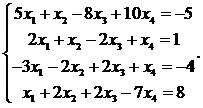
22. 
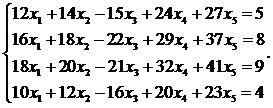
23. 
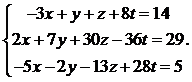
24.
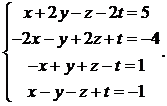
25.
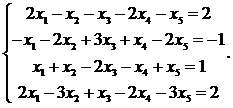
26. 
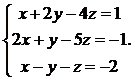
27. 
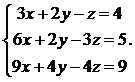
28. 
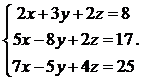
29. 
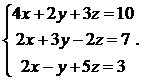
30. 
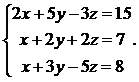
Задание №7
Найти фундаментальную систему решений и общее решение системы однородных уравнений
1. 
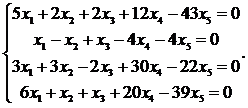
2. 
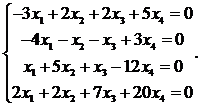
3. 
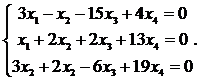
4. 
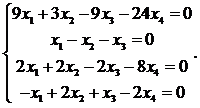
5. 
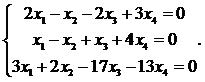
6. 
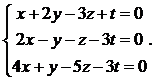
7. 
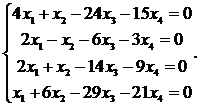
8. 
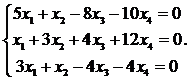
9. 
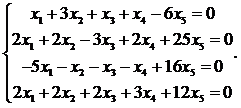
10. 
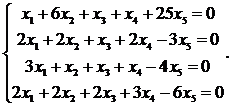
11. 
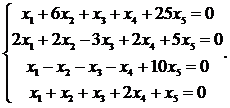
12. 
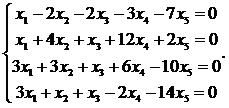
13.
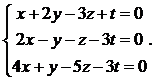
14.
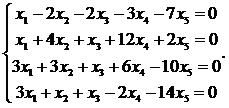
15. 
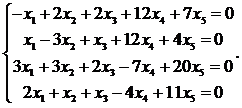
16. 
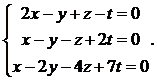
17. 
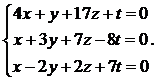
18. 
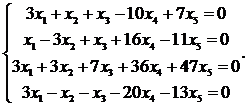
19. 
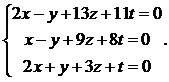
20. 
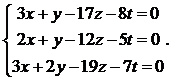
21. 
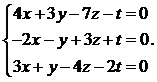
22. 
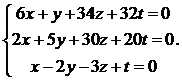
23. 
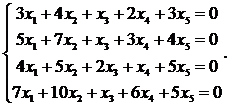
24. 
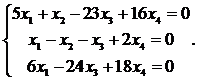
25. 
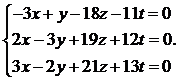
26. 
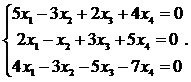
27. 
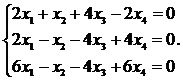
28. 
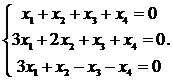
29. 
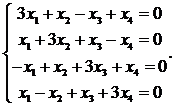
30. 