Алгоритм вычисления обратной матрицы

1. Находим определитель исходной матрицы А. Если |А|=0, то матрица А вырожденная и обратной матрицы А^-1 не существует. Если |А|¹0, то матрица А невырожденная и обратная матрица существует. Переходим к шагу 2.

2. Находим матрицу А^Т, транспонированную к А. Переходим к шагу 3.

3. Находим алгебраические дополнения элементов транспонированной матрицы 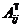=A_ji (i,j=1,2,...,п) и составляем из них присоединеннуюматрицу 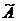: 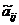= =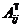A_ji (i,j=1,2,..., п). Переходим к шагу 4.

4. Вычисляем обратную матрицу по формуле А^-1= .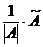

Для проверки правильности вычисления обратной матрицы А^-1, исходя из ее определения, рекомендуется проверить выполнение равенств AA^-1=A^-1A=E.

Пример 1. Найдём матрицу, обратную матрице А= .

n 1. Определитель матрицы |А|=7¹0 (см. пример 3 §1.3), т.е. матрица А – невырожденная и обратная матрица A^-1 существует.

2. Находим матрицу А^T, транспонированную к А: А^T= .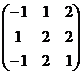

3. Находим алгебраические дополнения элементов матрицы А^T и составляем из них присоединенную матрицу:

А₁₁=(-1)¹⁺¹ 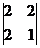=-2; А₁₂=(-1)¹⁺² 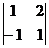=-3; А₁₃=(-1)¹⁺³ 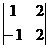=4 и т.д.,

= .

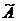4. Вычисляем обратную матрицу А^-1= :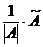

А^-1= = .

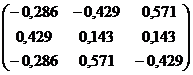Проверим, например, правильность формулы A^-1A=E:

A^-1A= = =

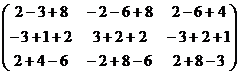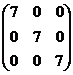= =E. l

5. Собственные значения и собственные векторы матрицы.Будем рассматривать квадратные матрицы размером п´п, или, что то же самое, матрицы порядка п.

При умножении матрицы порядка п та на п-мерный вектор в произведении получается п-мерный вектор:

Ах=у.

Для любой матрицы может существовать набор особых векторов, таких, что произведение матрицы на вектор из такого набора равносильно умножению этого вектора на определенное вещественное число (вообще говоря, разное для каждого вектора).

Определение 1. Число l называется собственным значением матрицы А порядка п, если существует такой ненулевой вектор хÎRⁿ, что выполняется равенство

Ах=lх. (1)

При этом вектор х называется собственным вектором матрицы А, а l – собственным значением матрицы А, соответствующим вектору.

Иными словами, умножение матрицы на ее собственный вектор равносильно удлинению этого вектора в |l| раз, если |l|>1 (или сжатию при |l|<1). Если l=1, умножение матрицы на соответствующий собственный вектор не меняет его. Уравнение (1) представлено в матричной форме. Группируя все слагаемые этого уравнения в левой части, перепишем его в более удобном виде:

(А-Е)х=0,

где Е и0 – соответственно единичная матрица и нулевой вектор.

Если a_ij – элементы матрицы А, тохарактеристическаяматрица А-lЕ, согласно определениям умножения матрицы на число и суммы матриц, имеет вид

А-lЕ= .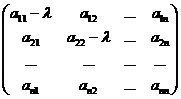

Система линейных уравнений

1. Системa из п линейных уравнений с п неизвестными.

Определение 1. Будем называть произвольную систему из п чисел =(х₁,…,х_п)^Тп-мерным вектором и обозначать его х=(х₁,…, х_п)^Т.

Зададим систему из из п линейных уравнений с п неизвестными

(1)

Числа а_uj (i,j=1,…,п) (действительные или комплексные), называемые коэффициентами системы (1), заданы. Будем ещё говорить, что система (1) определяется матрицей

А= = (2)

её коэффициентов.

Нас будет интересовать вопрос о разрешимости системы (1) для каждого вектора (столбца свободных членов) у=(y₁,…,y_n)^Т.

Определение 2. Вектор х=(х₁,…, х_п)^Т называется решением системы уравнений(1), если числа х_j удовлетворяют этим уравнениям. В этом случае говорят, что система совместна. Если при этом система имеет только одно решение, то она называется определённой. Если система вообще не имеет решений, то она называется несовместной.

Определение 3. Две системы называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.

Систему (1) можно записать в матричном виде

Ах=у. (3)

2. Метод обратной матрицы и формулы Крамера. Вычисление определителей в MathCAD. Для получения решения системы (1) п.1 в общем виде предположим, что матрица система невырожденная, т. е. её определитель ∆= ¹0. В этом случае существует обратная матрица А^-1. Умножая слева обе части матричного уравнения (3) п.1 на матрицу А^-1, получаем А^-1(Ах)=А^-1у. Так как

А^-1(Ах)=(А^-1А)х=Ех=х, то решением системы методом обратной матрицы будет матрица-столбец

х=А^-1у. (1)

Теорема 1 (Теорема Крамера). Пусть ∆= – определитель матрицы А системы (1) п.1, ∆_j – определитель, получаемый из определителя ∆, если в нём заменить числа j-го столбца соответственно на числа y₁,…,y_n:

∆_j= . (2)

Если определитель системы не равен нулю, ∆¹0, то система (1) п.1 имеет единственное решение для любого вектора у, вычисляемого по формулам (Крамера)

х_j=∆_j/∆ (j=1,…,п). (3)

Таким образом,

х_j= (j=1,…,п), (3¢)

где А_sj – алгебраические дополнения элемента а_sj в определителе ∆.

n Пусть (х₁,…, х_п) есть решение системы (1) п.1. Чтобы найти неизвестное число х₁, умножим 1-е уравнение системы (1) п.1на алгебраическое дополнение А₁₁, второе – на А₂₁, …, п-е – на А_п1 и сложим все уравнения системы. Тогда, учитывая, что

=х₁ =х₁∆

и

=х_j =х_j×0=0 (j¹1),

получаем х₁∆=∆₁, где

∆₁= = .

Следовательно, так как по условию ∆¹0, то х₁=∆₁/∆.

Аналогично получаем

∆ _j= = .

Отсюда в силу того, что ∆¹0, следует равенство (3).

Мы доказали, что если (х₁,…, х_п) есть решение системы (1) п.1, то числа х_j определяются равенствами (3¢).

Обратно, совокупность чисел х_j=∆_j/∆ (j=1,…,п) является решением системы (1) п.1. В самом деле, подставляя х_j (j=1,…,п) в левую часть k – го уравнения (k=1,…,п), на основании свойств 6, 7 определителей имеем:

= = = y_k∆=y_k.

Т. о., (3¢) действительно является решением системы (1) п.1. l

Замечание. Можно показать, что если определитель системы ∆= =0, а хотя бы один из определителей ∆_j¹0 (j=1,…,п), то система несовместна. Если же определитель ∆= =0 и все определители ∆_j=0 (j=1,…,п), то система либо несовместна, либо имеет бесконечное количество решений.

Пример 1. Решим систему уравнений

двумя способами: а) средствами матричного исчисления; б) по формулам Крамера.

n Исходную систему запишем в матричном виде Ах=у. Здесь матрица коэффициентов А= , х= , у= .Т.к. |А|=7¹0 (см. пример 1 §2.3), то матрица А невырожденная, и у неё существует обратная А^-1, найденная в примере 1 §2.4: А^-1= . Тогда по формуле (1) п.2

х=А^-1у= = = ,

т.е. х₁=1, х₂=-1, х₃=3.

б) Т.к. определитель системы |А|=7¹0, то по теореме Крамера система имеет единственное решение: х_j=∆_j/∆ (j=1,…,3). Вычислим определители ∆₁, ∆₂ и ∆₃, полученные из определителя ∆=|А| заменой соответственно 1-го, 2-го и 3-го столбцов столбцом свободных членов:

∆₁= =7, ∆₂= =-7, ∆₃= =21

(определители вычислены с помощью MathСAD, рис.1). Тогда по формулам Крамера (3) х₁= = =1, х₂= = =-1, х₃= = =3.

Вычисление определителей

Рис.1

После этого рекомендуется сделать проверку, подставив найденное решение в уравнения системы и убедившись в том, что они обращаются в тождества.

3. Метод последовательного исключения неизвестных (метод Гаусса).

Определение 1. Расширенной матрицей системы (1) п.1 называется матрица А₁= , полученная присоединением к А столбца свободных членов

у= .

Замечание 1. Обозначим рангматрицы А₁ через r₁ (r₁=ранг А). Т.к. матрица А – часть А₁, то её ранг не может быть больше рангаматрицы А₁, т.е. справедливо неравенство r£r₁.

Пусть дана система

(1)

Определение 1. Следующие преобразования матрицы называют элементарными преобразованиями:

1) Перестановка местами любых двух строк (столбцов).

2) Умножение всех элементов любых строк (столбцов) на число k¹0.

3) Умножение всех элементов любой строки (столбца) на постоянное число и прибавление их к соответствующим элементам другой строки (столбца).

4) Отбрасывание нулевой строки (столбца).

5) Транспонирование матрицы.

С помощью элементарных преобразований матрицы коэффициентов системы (1) п.1 получается система, равносильная данной.

Метод Гаусса заключается в том, что с помощью элементарных преобразований система уравнений приводится к системе ступенчатого вида, из которой последовательно, начиная с последних, находятся все остальные неизвестные.

Применяя подходящим образом элементарные операции над системой уравнений или, что всё равно, над расширенной матрицей , добиться либо решения заданной системы (1), либо прийти к явно противоречивой системе. Так как последняя эквивалентна системе (1), то это докажет противоречивость системы (1).

Ниже приводятся примеры применения этого метода.

Пример 1. Решим систему

n Конечно, согласно теореме Крамера, мы могли бы вычислить все пять определителей четвёртого порядка и найти х₁, х₂, х₃, х₄. Здесь было бы много повторяющихся вычислений.

Составим матрицу , = , где, как мы видим, последний столбец состоит из правых частей нашей системы. Умножая 1-ю строку на (-1) и прибавляя её к 3-й и 4-й строкам, получим матрицу ~ . Дальнейшие преобразования матриц очевидны:

~ ~ .

Последняя матрица эквивалентна системе

Тогда из 4-го уравнения х₄=2, из 3-го х₃= =-3, из 2-го х₂=-2-2х₃-3х₄=-2, из 1-го х₁=-1-2х₂-3х₃-4х₄=4. Чтобы не допустить ошибки, рекомендуется осуществить проверку, подставив полученные значения в исходные уравнения системы. l

Пример 2. Решим систему

n Имеем: = ~ ~ . Последняя строка полученной матрицы эквивалентна уравнению 0×х₁+0×х₂+0×х₃=3, что говорит о несовместности исходной системы. l

Пример 3. Решим систему

n Имеем: = ~ ~ ~

~ . Последняя матрица эквивалентна системе

то есть система имеет бесконечное множество решений:

х₄=С₂, х₃=С₁, х₂=- +С₁- С₂, х₁= - С₂,

где С₁, С₂ – любые числа (-¥<С₁, С₂<¥). l

4. Теорема Кронeкера-Капелли. Перейдём теперь к дальнейшему исследованию системы (1) п.1. Будем предполагать, что хотя бы один элемент её матрицы А не равен нулю и обозначим ранг матрицы А через r (r=ранг А). Таким образом, 1£r£п.

Теорема1 (Кронeкера-Капелли). Система (1) совместна тогда и только тогда, когда ранграсширенной матрицы А₁ равен рангуматрицы А (r₁=r). В этом случае r называется рангом системы.

Теорема2. Если ранг совместной системы равен числу неизвестных (т.е. r=п), то система является определённой. Если же r<п, то система неопределённа.

Теорема1 не означает, что для решения системы в общем случае необходимо вычислять отдельно, а затем сравнивать ранги матриц А и А₁. Для этого достаточно применить метод Гаусса для матрицы А₁. Метод Гаусса более универсален и значительно менее трудоёмок матричного метода и метода Крамера. Кроме того, метод Гаусса позволяет одновременно определить ранги матриц А и А₁ и найти решение системы, если оно существует.

Пример 1. Решим систему

n Имеем: = ~ ~ ~

~ ~ ~ . Ранг системы r равен 3, r=3. Матрица эквивалентна системе

.

то есть система имеет бесконечное множество решений. Пусть х₄=С. Тогда

х₁= + С, х₂=- + С, х₃=- + С, х₄=С,

где С – любое число (-¥<С<¥). l

Пример 2. Решим систему

n Имеем: = ~ ~ . При этом r(A)=2, т.к. её определитель (минор 3-го порядка) ∆=М₃= =0, а один из миноров 2-го порядка, например, М₂= =-10¹0. Ранг же матрицы равен 3, т.к. её один из миноров наивысшего, 3-го порядка, например, =-10¹0. Следовательно, по теореме Кронекера-Капелли система решений не имеет. l

Однородная система.

Определение 1. Система уравнений

(1)

называется однородной.

Эта система является частным случаем системы (1) п.1 при y₁=…=y_т=0. Т.к. расширенная матрица А₁ однородной системыотличается от матрицы А только нулевым столбцом правых частей, то эти матрицы эквивалентны, и их ранги равны. Поэтому для однородной системы теорема Кронекера-Капелли всегда выполняется, и она совместна. Ясно, что вектор х₁=…=х_п=0 удовлетворяет однородной системе (1).

Определение 2. Если однородная система (1) имеет решением ненулевой вектор х=(х₁,…, х_п), то есть вектор, имеющий хотя бы одну компоненту х_j¹0, то это решение называют нетривиальным решениемоднородной системы (1). Нулевой вектор называют тривиальным решениемоднородной системы (1).

Если в системе (1) т=п, а её определитель |А|¹0, то по теореме Крамера система (1) имеет только тривиальное решение. Следовательно, нетривиальное решение возможно лишь для однородных систем, в которых число уравнений меньше числа неизвестных или при их равенстве, когда определитель системы равен нулю. Таким образом, справедлива следующая теорема:

Теорема 1. Линейная однородная система имеет нетривиальное решение тогда и только тогда, когда её ранг меньше числа неизвестных, т .е. при r(A)<n.

Пример 1. Решим однородную систему

nИмеем: А= ~ ~ ~ . Ранг матрицы A равен 2, т.к. её один из миноров наивысшего, 2-го порядка, например, =-5¹0. Т.о., ранг меньше числа неизвестных, и система имеет нетривиальное решение. Последняя матрица эквивалентна системе

то есть система имеет бесконечное множество решений. Пусть х₃=С. Тогда

х₁=-С, х₂=С, х₃=С,

где С – любое число (-¥<С<¥). l

6. Нахождение ранга матрицы методом Гаусса.Следующие примеры иллюстрируют этот метод.

Пример 1. Найдём ранг матрицы = .

n Ясно, что ранг матрицы не больше 4 – минимального из её размеров. В данном случае а₁₁=1¹0. Умножая 1-ю строку на (-1) и прибавляя её к 3-й строке, получаем: А~ . Теперь, умножая 1-й столбец на соответствующие числа и прибавляя его к остальным столбцам, получим:

А~ .

Второй столбец уже состоит из нулей, кроме элемента а₂₂=1¹0. Умножая 2-й столбец на (-1) и прибавляя его к 4, 6, 7 столбцам, получим

А~ ~ ~ ~

~ ~ .

Определитель 4-го порядка последней матрицы не равен нулю, следовательно, её ранг, также как и ранг исходной матрицы, равен 4. l

В MathCAD ранг матрицы вычисляется с помощью функции rank (рис.1):

Рис.1

Пример 2. Найдём ранг матрицы = .

n ~ ~ ~ ~ ~

~ ~ ,

то есть ранг матрицы равен 2. l

Рассуждения в примерах 1 и 2 основаны на следующем общем утверждении: при элементарном преобразовании А~А¢ ранг матрицы сохраняется, то есть выполняется равенствоr(А)=r(А¢).