Взаимное расположение плоскости и прямой в пространстве

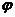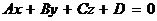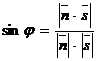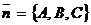■ Угол между прямой и плоскостью. Если прямая задана каноническими уравнениями (2), то угол ,образованный прямой с плоскостью , находится из соотношения , где – нормальный вектор плоскости, а 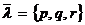– направляющий вектор прямой. (Заметим, что угол 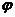между прямой и плоскостью всегда можно считать острым). В развернутом виде последняя формула имеет вид

.

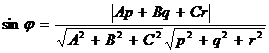Пример 1. Найти угол между прямой 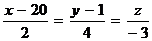и плоскостью .

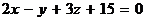Решение. Имеем 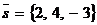, , 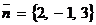поэтому

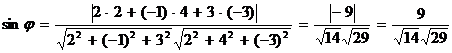, отсюда находим

.

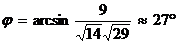■ Условие перпендикулярности прямой и плоскости. Очевидно, прямая перпендикулярна плоскости в том и только том случае, когда ее направляющий вектор 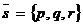коллинеарен нормальному вектору плоскости 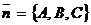. Поэтому условие перпендикулярности прямой и плоскости имеет вид (см. п. 2.3):

.

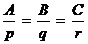Условие параллельности прямой и плоскости равносильно условию перпендикулярности векторов 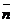и , которое, согласно п. 2.3, имеет вид 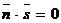или .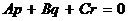

Пример 2. Составить канонические уравнения прямой, проходящей через точку М₀(1, -1, 4) и перпендикулярной плоскости .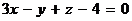

Решение. В качестве направляющего вектора прямой можно взять нормальный вектор плоскости 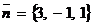, поэтому канонические уравнения прямой имеют вид .

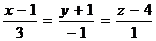Пример 3. Составить уравнение плоскости, проходящей через точку М₀(-3, 0, 2) и перпендикулярной прямой .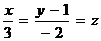

Решение. В качестве нормального вектора плоскости возьмем направляющий вектор 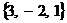данной прямой. Остается записать уравнение (1) из п. 2.6: .

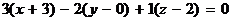Ответ: .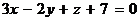

Пример 4. Найти точку пересечения прямой 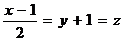с плоскостью .

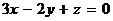Решение. Рассмотрим параметрические уравнения прямой: 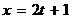, , 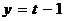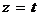; подставив эти выражения в уравнение плоскости вместо х, у, z,получим 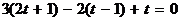, откуда 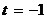. Искомые координаты точки пересечения: , , .

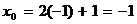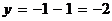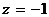Ответ: точка пересечения .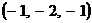

Пример 5. Найти проекцию точки М(3, -1, -1) на плоскость .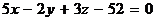

Решение. Составим параметрические уравнения прямой, проходящей через точку М перпендикулярно данной плоскости: 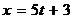, , 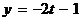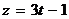(направляющим вектором этой прямой служит нормальный вектор {5, -2, 3} данной плоскости. Искомая проекция представляет собой точку пересечения плоскости с указанным перпендикуляром. Для ее нахождения подставим, как и в Примере 4, в уравнение плоскости найденные выражения х, у, z через параметр t: 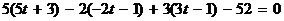; из этого уравнения находим 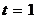. Поэтому искомые координаты проекции , , .

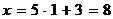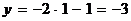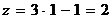Ответ: проекция точки М на плоскость: Р(8, -3, 2).

Пример 6. Лежат ли прямые 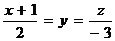и 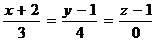в одной плоскости?

Решение.Введем вектор 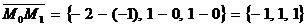. Здесь 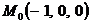– точка, через которую проходит первая прямая, а 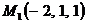– точка, через которую проходит вторая прямая (это легко усмотреть из канонических уравнений прямых). Направляющие векторы прямых: 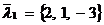, 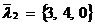. Наши прямые лежат в одной плоскости только в том случае, когда лежат в одной плоскости (компланарны) векторы 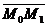, 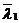и 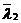. Но мы знаем, что условие компланарности трех векторов состоит в равенстве нулю их смешанного произведения (см. п. 2.5): 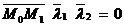. В нашем случае смешанное произведение равно 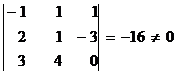. Таким образом, данные прямые не лежат в одной плоскости.