Прямолинейные образующие поверхности

Определение 43.Прямая называется прямолинейной образующей поверхности, если она целиком лежит на поверхности.

Очевидно, любая плоскость имеет бесконечно много прямолинейных образующих. Цилиндрические и конические поверхности, согласно их определению, тоже имеют бесконечно много прямолинейных образующих. Эллипсоид не может иметь прямолинейных образующих, т.к. он заключён внутри параллелепипеда.

Теорема 1. Эллиптический параболоид не имеет прямолинейных образующих.

Доказательство. Пусть q: Прямая q будет целиком лежать на эллиптическом параболоиде, заданном уравнением (91), тогда и только тогда, когда

уравнение удовлетворяется при любом значении t. Преобразовав его, получим . Этому уравнению удовлетворяет любое действительное число t тогда и только тогда, когда все его коэффициенты равны нулю, т.е. Отсюда следует, что m = n =р = 0, что невозможно, ибо m, n, р – координаты направляющего вектора прямой. Итак, никакая прямая не может целиком лежать на эллиптическом параболоиде.

Теорема 2.Двуполостный гиперболоид не имеет прямолинейных образующих.

Доказательство аналогично доказательству теоремы 1, проведите его самостоятельно.

Теорема 3. Однополостный гиперболоид имеет два бесконечных семейства прямолинейных образующих.

Доказательство. Пусть гиперболоид задан уравнением 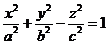. Отсюда , или Это уравнение, а следовательно и данное уравнение эквивалентно как уравнению (*), так и уравнению (**). Обозначая в (*) каждую дробь через a, получим, что уравнение (*), а поэтому и уравнение гиперболоида, эквивалентно системе Но эта система есть общие уравнения прямой. Так как a - любое действительное число, то получили бесконечное множество прямых, целиком покрывающих гиперболоид. Через каждую точку гиперболоида проходит точно одна из таких прямых.

Обозначая в (**) каждую дробь через b, получим, что уравнение (**), а поэтому и уравнение гиперболоида, эквивалентно системе Но эта система есть общие уравнения прямой. Так как b - любое действительное число, то получили бесконечное множество прямых, целиком покрывающих гиперболоид. Через каждую точку гиперболоида проходит точно одна из таких прямых. Очевидно первое и второе множества прямых – различные.

Итак, на однополостном гиперболоиде укладываются два бесконечных семейства прямолинейных образующих.

Теорема 4.На гиперболическом параболоиде лежат два бесконечных семейства прямолинейных образующих.

Доказательство. Уравнение (38) можно преобразовать к виду

.

Это уравнение эквивалентно как уравнению (*), так и уравнению (**). Уравнение (*) эквивалентно системе . При любом a эта система задаёт прямую. Получили семейство прямых, целиком покрывающих параболоид. Через каждую точку параболоида проходит точно одна прямая этого семейства. Уравнение (**) эквивалентно системе Получили второе семейство прямых, целиком покрывающих параболоид. Через каждую точку параболоида проходит точно одна прямая этого семейства.

Итак, на поверхности гиперболического параболоида лежат два бесконечных семейства прямолинейных образующих.

Пример 5. Найдите прямолинейные образующие гиперболического параболоида

Х² - 4У² = Z,

проходящие через точку М(-1, 2, -15).

Решение. Так как координаты точки М удовлетворяют данному уравнению, то эта точка лежит на данном параболоиде. Запишем уравнение в виде (Х - 2У)(Х + 2У) = Z×1, получим две пропорции и , каждая из которых эквивалентна данному уравнению. Эти пропорции, в свою очередь, эквивалентны соответственно системам уравнений (*) и (**), где a и b - любые действительные числа. Так как искомые образующие должны проходить через точку М, то координаты этой точки должны удовлетворять уравнениям этих образующих, т.е. и Отсюда a = , b = . Подставив (*) и (**), получим

и . После преобразований получим общие уравнения двух образующих, проходящих через точку М:

и

Литература

Основная литература

1. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1968.
2. Александров П.С. Лекции по аналитической геометрии. – М.: Наука, 1968.
3. Бахвалов С.В., Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии. – М.: Наука, 1964.

Дополнительная литература

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Физматлит, 2000.

2. Постников М.М. Аналитическая геометрия. – М.: Наука , 1974.

3. Атанасян Л.С., Базылев В.Т. Геометрия. Часть 1. – М.: Просвещение, любой год издания.

4. Цубербиллер О.Н. Сборник задач и упражнений по аналитической геометрии, издание 27. – М.: Физматгиз, 1970.

Методические пособия

1. Аналитическая геометрия. Лабораторные работы (8 работ). -_Пермь: ПГУ, 2003.

2. Практикум по геометрии. Разделы: «Векторное и смешанное произведения векторов», «Метод координат в пространстве». – Пермь: ПГПУ, 2002

3. Тесты по аналитической геометрии:

-Векторная алгебра, части 1 и 2.

-Прямая на плоскости. Плоскость в пространстве.

-Прямая в пространстве.

-Прямая и плоскость в пространстве.

-Элементарная теория кривых 2-го порядка.