Бинарная агебраическая операция. нейтральный элемент. ассоциативная алгебраическая операция. симметрический элемент.

Пусть Х не пустое множество, X² — скалярный квадрат множества X, т.е. X²={(a,b)| a,bÎX}.

Определение 1.Отображение f:X²®X называется бинарной алгебраической операцией (БАО), то есть каждой паре элементов (a,b) множества X ставится в соответствие элемент сÎX.

Элемент c называется композицией элементов a и b, обычно записывают c=a°b (где ° — обозначение кокой-то бинарной алгебраической операции).

Примеры:

1) Вкачестве множества X возьмем N — натуральные числа, в качестве операции +:

(a,b)®a+b — отображение и

c=a+b — сумма.

2) Множество матриц над полем P с операциями +, *.

Если X — конечное множество, например X={x₁, x₂, ¼ ,x_n}, то алгебраическую операцию удобно задавать таблицей:

	x1 x2 x3 … xn
x1
x2 x3 … xn

В клетке этой таблицы, расположенной на пересечении строки, проходящей через элемент ak, и столбца, проходящего через элемент al, следует записать композицию элементов ak и al.

Часто алгебраическую операцию называют внутренним законом композиции.

Определение 2.Пусть заданы множество X с бинарной алгебраической операцией °, и любое его непустое подмножество X₁. Если "a,b'X₁ a°b тоже принадлежит X₁ ,то множество X₁ называют устойчивым относительно данной бинарной алгебраической операции, а саму бинарную алгебраическую операцию на X₁ называют индуцированной.

Определение 3.Пусть на множестве Х задана бинарная алгебраическая операция ° (дальше для краткости просто операция °). Элемент hÎХ называется нейтральным относительно операции °, если x°h=h°x=x "xÎX.

Примеры.

1) В операции умножения на множестве целых чисел Z роль нейтрального элемента играет 1.

2) На множестве 2Z нет нейтрального элемента относительно умнажения.

Теорема 1.Относительно любой алгебраической операции существует не более одного нейтрального элемента.

Доказательство (от противного). Пусть m и n нейтральные элементы относительно операции ° на X, причем m¹n. Тогда по определению нейтрального элемента:

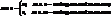Þ m=n.

Определение 4.Алгебраическая оперция °, заданная на множестве X, называется ассоциативной, если "a,b,cÎX выполняется: (a°b) °c=a°(b°c).

Теорема 2.Пусть на множестве Х задана ассоциативная операция °, тогда:

(a₁°…°a_i) °(a_i+1°…°a_n )= a₁°…°a_n

Доказательство индукцией (по числу элементов во второй скобке):

1) Если n – i=1, то равенство верно по определению.

2) Если n - i=k, то будем считать утверждение верным.

3) Докажем верность для n - i=k+1.

(a₁°…°a_i)°(a_i+1°…°a_n )= (a₁°…°a_i)°((a_i+1°…°a_n-1 ) °a_n ) так как операция ° ассоциативна, то по-другому расставим скобки и воспользуемся индуктивным предположением

(a₁°…°a_i)°((a_i+1°…°a_n-1 )°a_n )= =((a₁°…°a_i)°(a_i+1°…°a_n-1 )) °a_n = a₁°…°a_n .

Следствие.Пусть на множестве Х задана ассоциативная операция °. Тогда композиция конечного числа элементов множества Х не зависит от распределения скобок, указывающих на порядок производимых действий.

Определение 5.Пусть на множестве Х задана операция °, n – нейтральный элемент и x,y —некоторые элементы из множества Х. Элемент y называется симметричным элементу x относительно операции °, если x°y=y°x=n. Если для элемента x есть симметричный, то он называется симметризуемым.

Примеры:

1) На множестве целых чисел, операция +, n=0, симметричный элемент элементу a — противоположный -a.

2) Множество матриц над полем P_n, E — единичная матрица (нейтральный элемент при умножении). Симметричный элемент существует тогда, когда матрица обратима, т.е ее определитель не равен нулю.

Теорема 3.Пусть на множестве X задана ассоциативная операция ° и n — нейтральный элемент. Тогда "xÎX существует не более одного симетричного элемента.

Докозательство (от противного).

Пусть для некоторого элемента x существует несколько симметричных элементов, например: y,z. Тогда рассмотрим композицию: y°x°z=y°(x°z)=y°n=y, с другой стороны y°x°z=(y°x)°z)=n°z=z Þ y=z.

Симметричный для x обозначим через x'.

Теорема 4.Пусть на множестве X задана ассоциативная операция °. Элементы x,yÎX — симметризуемы, тогда элемент x°y также симметризуем и симметричный для него (x°y)'= y'° x'.

Доказательство. Рассмотрим композицию: (x°y)°( y'° x')=x°(y°y') °x'=x°x'=n, где n – нейтральный элемент. Аналогично (y'°x') ° (x°y)=n.

Определение 6.Операция ° называется коммутативной, если x°y=y°x "x,yÎX.

35-36.

ОПРЕДЕЛЕНИЕ ГРУППЫ, ВАЖНЫЕ ПРИМЕРЫ И СВОЙСТВА ГРУПП

Определение1.Пусть Г не пустое множество элементов произвольной природы. Г называется группой, если выполняются следующие условия:

1) На множестве Г задана операция °.

2) Операция ° ассоциативна.

3) Существует нейтральный элемент nÎГ.

4) Для любого элемента из Г симметричный ему элемент всегда существует и принадлежит также Г.

Пример.

Множество Z – чисел с операцией +.

Определение 2.

Группа называется абелевой, если она коммутативна относительно заданной операции °.

Важные примеры групп

1) GL(n,P) — полная линейная группа над полем P степени n. Рассмотрим множество матриц порядка n над некоторым полем P, определитель которых отличен от нуля: GL(n,P)={A Î P_n , |A|¹0}. Проверим, что это группа:

1. Операция ° задана, ибо произведение невырожденных матриц — невырожденная матрица;

2. Операция ° ассоциативна, ибо произведение матриц ассоциативно;

3. Существует нейтральный элемент — единичная матрица;

4. Обратная матрица существует и принадлежит GL(n,P), а это и есть симметричный элемент.

2) SL(n,P)={AÎP_n , |A|=1} — специальная линейная группа степени n над полем. Это множество матриц над полем P порядка n, с определителем равным 1.

1. Операция ° задана, ибо |AB| = |A||B|=1;

2. Операция ° ассоциативна;

3. Существует нейтральный элемент — единичная матрица, ибо |E|=1;

4. Существует элемент симметричный 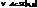— обратная матрица, так как определитель не равен нулю, и она принадлежит SL(n,P).

3) S(X) — симметричная группа на множестве X, где X — не пустое множество, S(X) — множество биективных отображений из X в X. Тождественное отображение принадлежит 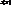, следовательно, S(X) ¹Æ

1. Операция ° задана, ибо произведение биективных отображений — биективное отображение;

2. Операция ° ассоциативна, ибо произведение отображений ассоциативно;

3. Существует нейтральный элемент e_x (тождественное отображение на X);

4. Существует обратное отображение, для любого биективного отображения и оно принадлежит S(X).

Если X — конечное множество и состоит из n элементов |C|=n, то в этом случае S(X) обозначается S_n , так как природа элементов не существенна, то полагаем Х={1,…,n}.

4) Рассмотрим множество четных подстановок A_n на множестве из n элементов. A_n ¹Æ, ибо тождественное отображение принадлежит A_n.

1. Операция ° задана (произведение четных подстановок— четная подстановка);

2. Операция ° – ассоциативна;

3. Тождественная подстановка играет роль единицы;

4. Для любой подстановки из A_n существует обратная подстановка (она тоже четная).

A_n — знакопеременная группа степени n.

Простейшие свойства групп

В группе существует единственный нейтральный элемент

В группе для каждого элемента существует единственный симметричный ему элемент

Пусть Г — группа с операцией °, тогда уравнения вида :

a°x=b и x°a=b (1) — разрешимы и имеют единственное решение.

Доказательство. Рассмотрим уравнения (1) относительно x. Очевидно, что для а $! а'. Так как операция ° — ассоциативна, то очевидно x=b°a' — единственное решение.