Деление многочленов.теорема о делении с остатком.

Лемма: Пусть f(x), g(x) ÎР[x] — многочлены; f(x) ¹0, g(x) ¹0.

Тогда deg f(x)* g(x)= deg f(x)+deg g(x).

< Пусть f(x)=a0+a1x+…+an x^n , аn¹0,

g(x)=b0+b1x+…+bs x^s , bs¹0

f(x)* g(x)=an*bs x(^n+1)+…

Последнее и означает, что степень многочлена равна n+s.

deg f(x)* g(x)=n+s.>

Определение1.Пусть f(x), g(x)ÎР[х]. Будем говорить, что f(x) делит g(x) (обозначать f(x)ïg(x) ), если существует j(х)ÎР[х] такое,что g(x)=f(x)*j(х).

Простейшие свойства:

1)Если g(x) делит fi(x), i=1..n, то g(x) делит .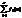

2)Если f(x) / g(x)и g(x) / m(x), тогда f(x) / m(x).

3)Если f(x) / g(x)и g(x) / f(x), то f(x)=ag(x),где aÎР.

Докажем первое свойство:

◄g(x) / fi(x) следовательно $ многочлен ji(х), что fi(x) = g(x)ji(х), следовательно

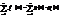
Вынесем общий множитель g(x) за знак суммы. А это и означает, что g(x) делит сумму . >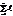

Второе свойство доказывается аналогично как и для чисел.

Докажем третье свойство:

< f(x) / g(x)®g(x)=f(x)*m(x) (1)

g(x) / f(x)®f(x)=g(x)*q(x) (2)

Подставим (2) в (1):

g(x)=g(x)*q(x)*m(x) Þ g(x)*(q(x)*m(x)-1)=0Þq(x)*m(x)=1.

Из леммы следует, что степень q(x)= степени m(x)=0.

Иначе говоря, что q(x) и m(x) — это элементы поля P. А это и доказывает свойство 3. >

Теорема о делении с остатком:Пусть f(x), g(x)ÎР[х], g(x)¹0. Тогда существует единственная пара многочленов q(x), r(x)ÎР[х], такая, что f(x)=g(x)*q(x)+r(x), где степень r(x)<степени g(x)либо r(x)=0.

Доказательство. 1) случай: f=0,очевидно q=0, r=0; 2) случай: если степень f<степени g(cт.g), то q=0 и r=f; 3)случай: ст. f³ст.g.

Пусть

f=an*x^n+…+a0,

g=bs*x^s+…+b0.

Возьмем многочлен j1=(an/bs)*x(s-n). Рассмотрим f-g*j1=f1. Если f1=0, то в качестве r возьмём 0, в качестве q-j1, т.е. r=0; q=j1. Если ст. f1 < ст.g , то в качестве r возьмем f1, а в качестве q -j1. Если ст. f1³ ст.g, то берем

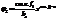
f – g j1 ₌ f1 ( ст.f1 < ст.f ),

f – g j2 ₌ f2 ( ст.f2 < ст.f2 ). C f2 рассуждаем аналогично как и с f2. На

каком-то шаге мы получим, что многочлен fk=0 либо его степень меньше степени g ( степени многочленов f_k все время уменьшаются ), где f_k-1 – g (j)(k) = fk

f – g j1 ₌ f1 ( ст.f1 < ст.f ) Сложим почленно

f1 – gj2 ₌ f2 ( ст.f2 < ст.f1 ) (1) левые и правые части

…………………………..

равенств:

f_k-1 – g (j)(k) ₌ fk

__________________________

Получим, что

f – g (j1+…+jk ) = fk и очевидно

q = j1+…+jk ; r = fk.

Этим мы доказали существование q и r.

f = g(j1+…+jk ) + fk.

Докажем однозначность q и r. Доказывать будем методом от противного. Пусть наряду с разложением f = gq+r (2) имеет место разложение f = gq1+r1 (3). Вычтем из (2) равенство (3). Получим:

r – r1 = g ( q1 – q ).

Сравним степени многочленов слева и справа. Если r-r1≠0, то степень r – r1 < степени -g (q1 – q ). А такого быть не может для равных многочленов. Мы пришли к противоречию. Однозначность доказана. >

Алгоритм Евклида: Пусть f(x) и g(x) — два многочлена над полем Р.

f(x) , g[x] ÎP[x] ; g(x)¹ 0. Тогда можно разделить с остатком f(x) на g(x).

f(x)=g(x)q(x)+r(x) , если r(x) ¹0, степень r(x)<степени g(x).

Разделим g(x) на r(x) с остатком g(x)=r(x)q1(x)+r1(x), если r1(x) ¹0 степень r₁ < степени r.

Разделим r(x) на r1(x) и т.д.

Так как степени остатков все время убывают, то на каком-то шаге остаток r_k+1(x)=0.

f(x)=g(x)q(x)+r(x) ; r(x) ¹0

g(x)=r(x) q1(x)+r1(x) ; r1(x) ¹0 ; cт. R1< ст. r

(4) r(x)=r1(x)q2(x)+r2(x)

…………………..

(r)(k-1) (x)=rk(x)(q) (k+1)(x)+ (r)(k+1) (x), (r)(k+1) (x)=0.

Процесс последовательного получения равенств (4) называют алгоритмом Евклида для многочленов f(x) и g(x). Последний отличный от нуля остаток — rk.

23 - 24

HOД МНОГОЧЛЕНОВ.

ВЗАИМНО ПРОСТЫЕ МНОГОЧЛЕНЫ.

Определение 1. Пусть f1(x), … , fk(x)Î P[x] и Е fi(x)¹ 0 (ненулевой набор многочленов). Если $ многочлен d(x) ÎP[x] такой, что:

1) старший коэффициент d(x) равен 1.

2) d(x) / fi(x) " i=1,…,k

3) если h(x) ÎP[x] обладает свойством h(x) / fi(x) "i , то h(x) / d(x), тогда d(x) называют НОД многочленов fi,…, fk

Обозначим НОД многочленов f1,…, fk через ( f1,…, fk).

Выясним вопрос существования, однозначности и нахождения НОД.

Лемма 1: Пусть f1(x), … , fk(x)Î P[x],

М={ f1 j1+…+ fk jk | j1 ,…, j1 Î P[x] } — подмножество P[x]. f, g ÎM ; u, v ÎP[x] Þ fu+gv ÎM.

< f=f1j1+…+ fkjk g = f₁ 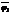+… +f_k 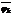fu+gv= f1(j1 u+ 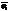v)+…+ fk(jk u+ 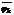v) очевидно из М. >

Теорема 1. ( О существовании НОД)

Пусть f1(x), … , fk(x)Î P[x] — некоторые многочлены, среди них есть ненулевой. Тогда многочлен наименьшей степени из М, взятый со старшим коэффициентом 1, является наибольшим общим делителем этих многочленов.

< Сразу же заметим, что в М есть ненулевой многочлен — fi(x). Докажем, что все fi(x) r=1,…,k в множестве М. По определению М

f1 j1+…+ fk jk Î М, если j1=1 ; j2=…=jk=0 ; Þf1ÎM и т.д.

Очевидно также, что в М есть многочлены со старшим коэффициентом 1 (см. Лемму1):

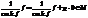
если f, g Î M.

Среди многочленов со старшим коэффициентом 1 выберем многочлен наименьшей степени. Обозначим его через d(x) и докажем, что это НОД. Во-первых, он со старшим коэффициентом 1 (мы его так выбрали).

Во-вторых, d(x) / fi(x) " i. (1)

Докажем (1). Допустим, что Ei d(x) ∤ fi(x) , т.е d(x) не делит fi(x). Разделим с остатком fi (x) на d (x): fi(x)=d(x)q(x)+r(x). Выразим r(x):

r(x)= f_i(x)+d(x)(-q(x)) Î M.

Согласно Лемме о делении с остатком ст.r < ст.d(x).

Если старший коэффициент r(x) равен 1, то сразу же имеем противоречие с выбором d, если же старший коэффициент не равен 1, сделаем, чтобы он стал равен 1:

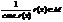(согласно Лемме 1)

Опять пришли к противоречию.

Докажем условие 3) в определении НОД.

Пусть h(x) | fi(x) " i d(x)= f1 j1+…+ fkjk ÎM Þ h(x) | d(x) (h(x) делит каждое из слагаемых, значит он делит сумму). >

Следствие (основное свойство НОД):

Наибольший общий делитель ненулевого набора многочленов f1, f2, …, fk представляется в виде: f1 y1,…,fn yk, где y1,…,ynÎP[x] .

Это следует из способа доказательства теоремы о существовании НОД, ибо НОД –элемент из М.

Теорема 2.НОД определен однозначно.

<Пусть d₁ и d₂ — наибольшие общие делители многочленов f1,…,fk.

Тогда d₁ делит f1,…,fk, то есть d₁ │ f1,…,fk, отсюда следует, что d₁ / d₂ ( по 3 свойству НОД). Аналогично d1 │ d2 ,значит можно записать d1 = a d2 . А так как d1 и d2 со старшим коэффициентом 1,то в качестве a можно взять только единицу (a=1). Значит d1=d2 ,т.е. НОД определен однозначно. >

Лемма 2.Пусть f(x)=g(x)q(x)+r(x).Тогда наибольший общий делитель f и g равен наибольшему общему делителю g и r, т.е.: ( f, g )=( g, r ).

< Доказательство теоремы следует из определения. Пусть ( f, g ) = d1 , ( g, r) = d2 .Тогда:

d1 │ f d2 │ g

Þ d1│ r Þ d1 │ d2 и d2 │ d1 Ü d2 │ f Ü

d1 │ g d2│ r

А значит: d1= d2. >

Теорема 3 (об отыскании НОД для двух многочленов).

Пусть f(x), g(x)ÎP[x], g(x)¹0. Тогда НОД многочленов f и g равен последнему, отличному от нуля, остатку в алгоритме Евклида для этих многочленов, взятому со старшим коэффициентом — единица. Если g | f, то НОД ( f, g ) равен .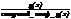

< Если g / f ,то последнее утверждение в формулировке теоремы очевидно

Применяя Лемму 2 к системе равенство (4) предыдущего параграфа, получим ,что

( f, g )=(g,r)=…=( r_k ; r_k-1 )=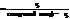

P.S. f=gq+r

g=rq₁+r₁

…………. система (4)

r_k-2=r_k-1+r_k

r_{k-1 =}r_kq_k+1+0. >

Замечание:

В теореме 3 содержится алгоритм практического отыскания НОД:

+ Ищем последний отличный от нуля остаток в алгоритме Евклида.

+ Делаем его со старшим коэффициентом единица ,это и будет НОД.

Теорема 4.(f1,……….,fk)=((f1,……..,(f)(k-1)) , fk ), k≥2.

Эта теорема указывает путь, как процесс нахождения НОД для нескольких многочленов можно свести к нахождению НОД двух многочленов.

Определение.Многочлены f_{1,……….,}f_k называются взаимно простыми, если их НОД равен единице.

Теорема 5(критерий взаимной простоты).

Многочлены (f1,………., fk ) взаимно простоты тогда и только тогда, когда $ u1,……,uk ÎP[x], такие что единица представляется в виде f1 u1 +……+fk uk.

<

Þ Имеем f1,……….,fk взаимно простые, то $ u1,……,uk ÎP[x], такие что f1u1 +……+fkuk=1. Это следует из основного свойства НОД.

Ü Пусть d(x)=( f1,……….,fk ). Значит d(x) | 1 Þ d(x)=1 и значит многочлены взаимно простые.>