Основные теоремы о степенях с одинаковым основанием

Алгебра.

Тема 1: «Повторение. Рациональные выражения. Сложение и вычитание рациональных дробей».

Урок 1:Повторение. Степень с натуральным показателем и ее свойства.

На данном уроке мы вспомним основные определения и свойства степени с натуральным показателем, кроме того, вспомним все основные теоремы и решим различные примеры, чтобы закрепить данную тему.

1. Основные определения

Вспомним основные определения:

– степень с натуральным показателем, здесь а – основание степени, n – показатель степени.

n штук

Кроме того, напомним, что:

и ;

Символ , как и символ не имеет смысла.

Все одночлены, многочлены и основные операции с ними основаны на степенях и действиях со степенями, которые мы сейчас вспомним:

Основные теоремы о степенях с одинаковым основанием

Основные теоремы о действиях со степенями:

;

Для того чтобы умножить степени с одинаковым основанием, нужно сложить их показатели, основание оставить тем же самым.

;

Можно разделить степени с одинаковым основанием, для этого их показатели нужно вычесть, а основание оставить тем же самым;

Пример 1:

;

Для того чтобы степень возвести в степень, нужно перемножить показатели степени, основание оставить без изменений.

Основные правила работы со степенями с одинаковым показателем

Мы вспомнили основные правила работы со степенями с одинаковым основанием. В качестве примеров выведем еще несколько правил:

Пример 2: – возвести минус единицу в четную степень; – возвести минус единицу в нечетную степень;

– при возведении в квадрат любое число станет положительным, единица в любой степени равна единице, таким образом, независимо от значения выражение равно единице.

В предыдущем примере мы показали, что выражение всегда равно единице. Получаем:

Минус единица в первой степени равна сама себе, получаем:

Рассмотрим теперь правила обращения со степенями с одинаковым показателем:

;

При умножении степеней с одинаковыми показателями, нужно перемножить основания и возвести результат в исходную степень;

, ;

Чтобы разделить степени с одинаковыми показателями, нужно разделить основания и возвести результат в исходную степень;

Пример 3:

Итак, в числителе и знаменателе перемножим степени с одинаковым основанием:

Возведем в числителе и знаменателе степень в степень:

Выполним деление степеней с одинаковым основанием:

Чтобы получить результат, выполним некоторые преобразования:

4. Решение вычислительных примеров

Пример 4: вычислить:

Чтобы решить данный пример, все основания степеней нужно привести к самому простому:

, ,

Итак, получаем:

Выполним возведение степени в степень:

Выполним сокращение дроби:

Вычислим:

Выводы по уроку

Вывод: на данном уроке мы вспомнили основные определения касательно степени с натуральным показателем и ее основные свойства. Записали теоремы и решили примеры на их применение.

Домашнее задание.

1. Найдите значение выражения: .

2. Выполните действия: а) ; б) ; в) ; г) .

3. Вычислить: а) ; б) .

4. Известно, что . Найдите значение выражения: а) ;

б) .

Урок 2:Повторение. Одночлены.

На данном уроке мы вспомним основные теоретические понятия, касающиеся одночленов, и теоремы о степенях, на которой они базируются. Мы вспомним основные типовые задачи и рассмотрим примеры их решения.

Выводы по уроку

Вывод: на данном уроке мы вспомнили основные определения и свойства одночленов, типовые задачи, с ними связанные. Мы решили различные примеры, чтобы вспомнить и окончательно закрепить технику работы с одночленами.

Домашнее задание.

1. Преобразуйте выражение в одночлен стандартного вида: а) ; б) .

2. Упростите выражение: .

Урок 3:Повторение. Многочлены.

На данном уроке мы вспомним определение многочлена и приведение его к стандартному виду. Также вспомним основные арифметические операции над многочленами и решим типовые задачи.

Решение типовых задач

Одна из типовых задач – текстовые задачи, где нужно сначала составить уравнение, а потом его решить.

Пример 5: найдите 4 последовательных натуральных числа, если известно, что разность между произведением двух больших и двух меньших чисел равна 58.

Для решения задачи применим метод математического моделирования.

Этап 1 – составление математической модели:

Обозначим первое из четырех чисел за , тогда остальные числа запишем как , , , так как первое из четырех последовательных натуральных чисел является наименьшим, а каждое следующее отличается от предыдущего на единицу. Произведение двух больших чисел в таком случае равно , а произведение двух меньших – . В условии сказано, что разность между произведением двух больших и двух меньших чисел равна 58. Составим уравнение:

Математическая модель составлена.

Этап 2 – работа с математической моделью:

В данном случае работа заключается в решении линейного уравнения с одним неизвестным. Для этого упростим составленное выражение, выполним умножение:

Соберем неизвестные слева, а свободные члены – справа и приведем подобные:

Из полученного элементарного уравнения найдем n:

Этап 3 – ответ на вопрос задачи:

Было задано найти четыре последовательных натуральных числа, удовлетворяющих условию. Первое из чисел мы обозначили за n, нашли , таким образом, нужная нам последовательность – это числа: 13, 14, 15, 16.

Выводы по уроку

Вывод: на данном уроке мы вспомнили определение многочлена и основы работы с многочленами – приведение к стандартному виду и арифметические операции. Кроме того, мы рассмотрели типовые задачи – вычислительную, текстовую задачи и уравнение.

Домашнее задание.

1. Найти сумму и разность многочленов:

а) (х² + 4х) – (х² – 4х); б)(5х² + 3х) + (х²-7 – 3х);

в) (х³ + 1,3х² - 2х) – (1,3х + 2х²).

2. Выполнить действия:

а) –х(х² - 3х); б) (х – 2)(х + 3); в) 16а³ - 2а²(8а – 3);

г) (9 + а² - 3а)(а² + 3а).

3. Решить уравнение:

а) ; б) (3 – х)(х + 4) + х² = 0.

4. Упростить выражение: .

Урок 4:Повторение. Формулы сокращенного умножения.

На данном уроке мы вспомним формулы сокращенного умножения, их предназначение и смысл. Мы решим несколько примеров на закрепление материала.

Итоги урока

Вывод: мы рассмотрели формулы сокращенного умножения, записали вид основных из них и некоторые доказали. Мы рассмотрели примеры различной сложности, чтобы окончательно закрепить данный материал.

Домашнее задание.

1. Преобразовать выражение в многочлен:

а) (а – 2)(а + 2); б) (7а + 8в)²; в) (с³ – 0,1)².

2. Решить уравнение:

(4х – 5)² = 16х² - 15.

3. Упростить выражение и найдите его значение:

а) (х – 2)(х + 2) – (х – 5)² при х = - 20; б) (3а + 1)(9а² - 3а + 1) при а = - .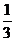

Урок 5:Повторение. Разложение многочленов на множители.

На данном уроке мы вспомним все изученные методы разложения многочлена на множители, рассмотрим примеры к ним.

1. Методы разложения многочленов на множители.

Напомним, что многочлен есть алгебраическая сумма одночленов, а одночлен – это произведение чисел и степеней.

Вспомним способы разложения многочлена на множители.

1. В каждом члене многочлена может быть общий множитель, отсюда первый способ – метод вынесения общего множителя за скобки, то есть такого множителя, который присутствует во всех членах многочлена. Рассмотрим пример 1, вынесем общий множитель за скобки, для этого определим, какие переменные представлены во всех членах, и вынесем их в минимальной степени:

;

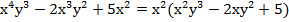Напомним, что, перемножив вынесенный множитель на скобку, можно проверить правильность вынесения.

Пример 2:

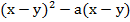
В обоих членах есть скобка 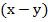, в одном в первой, а в другом во второй степени, вынесем минимальную ее степень – первую:

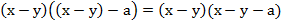
2. Метод группировки. Не всегда в многочлене можно вынести общий множитель. В таком случае нужно его члены разбить на группы таким образом, чтобы в каждой группе можно было вынести общий множитель, и постараться разбить так, чтобы после вынесения множителей в группах появился общий множитель у всего выражения, и можно было бы продолжить разложение. Рассмотрим пример 3:

;

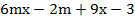Сгруппируем первый член со вторым, третий с четвертым и вынесем общие множители в группах:

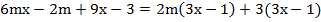
У выражения появился общий множитель. Вынесем его:

;

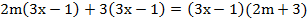3. Применение формул сокращенного умножения. Рассмотрим пример 4:

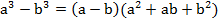
Мы расписали заданный многочлен по известной формуле разности кубов.

Пример 5:

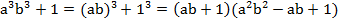
Комментарий: мы увидели в заданном многочлене формулу суммы кубов и разложили его.

4. Метод выделения полного квадрата. Он базируется на формулах квадрата суммы и квадрата разности. Напомним их:

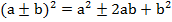– формула квадрата суммы (разности);

Особенность этих формул в том, что в них есть квадраты двух выражений и их удвоенное произведение. Рассмотрим пример 6:

;

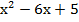Распишем выражение:

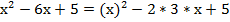
Итак, первое выражение – это 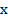, а второе должно быть 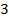, но не хватает удвоенного произведения. Прибавим и вычтем его:

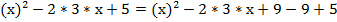
Свернем полный квадрат разности:

;

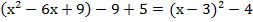Преобразуем полученное выражение, применяя формулу разности квадратов, напомним, что разность квадратов двух выражений есть произведение суммы на их разность:

;

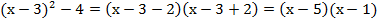Напомним, что, перемножив скобки, можно проверить правильность разложения.

Подведение итогов урока

Вывод: мы вспомнили все изученные методы разложения многочленов на множители и рассмотрели примеры. Вспомнили определение и некоторые свойства алгебраических дробей, решили несколько типовых задач, с ними связанных.

Домашнее задание.

1. Вынести общий множитель за скобки:

а) 8х – 8у; б) 5ху – 7х; в) 25х³ – 10х² + 5х;

г) 24а³у¹² – 12а²у¹º.

2. Решить уравнение:

а) (7х – 10)(х + 5) = 0; б) 12у² – 60у = 0; в) х³ + х² – 4х – 4 = 0.

3. Докажите, что выражение:

а) 5¹³ – 5¹¹ делится на 24; б) 125³ + 625² делится на 6.

4. Разложите на множители способом группировки:

а) 3(а + с) + х(а + с); б) 6х – 6у + ах – ау;

в) 2х¹¹ + 5х¹º – 2х² – 5х.

Урок 6: Повторение. Сис­те­мы двух ли­ней­ных урав­не­ний с двумя пе­ре­мен­ны­ми.

1. Определение системы уравнений с двумя переменными

На­пом­ним, что из себя пред­став­ля­ет си­сте­ма двух ли­ней­ных урав­не­ний с двумя пе­ре­мен­ны­ми. Это си­сте­ма вида:

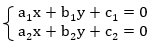
Из пер­во­го урав­не­ния 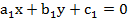можно по­лу­чить ли­ней­ную функ­цию, в слу­чае если 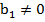: 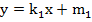. Гра­фик дан­но­го урав­не­ния – пря­мая линия.

Bто­рое ли­ней­ное урав­не­ние:

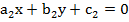, из него также можно по­лу­чить ли­ней­ную функ­цию, при усло­вии, что 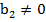: 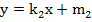. Гра­фик дан­но­го урав­не­ния – также пря­мая линия.

За­пи­шем си­сте­му в дру­гом виде:

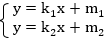
Мы знаем, что мно­же­ством ре­ше­ний пер­во­го урав­не­ния яв­ля­ет­ся мно­же­ство точек, ле­жа­щих на со­от­вет­ству­ю­щей ему пря­мой, ана­ло­гич­но и для вто­ро­го урав­не­ния мно­же­ство ре­ше­ний – это мно­же­ство точек на дру­гой пря­мой. Две пря­мые могут пе­ре­се­кать­ся – и тогда у си­сте­мы будет един­ствен­ное ре­ше­ние, един­ствен­ная пара чисел х и у будет удо­вле­тво­рять од­но­вре­мен­но обоим урав­не­ни­ям. Это про­ис­хо­дит, если 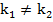. Две пря­мые также при неко­то­рых зна­че­ни­ях чис­лен­ных па­ра­мет­ров могут быть па­рал­лель­ны, в таком слу­чае они ни­ко­гда не пе­ре­се­кут­ся и не будут иметь ни одной общей точки, зна­чит в этом слу­чае си­сте­ма не будет иметь ре­ше­ний. Для этого долж­ны вы­пол­нять­ся усло­вия: 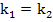и 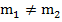. Кроме того, две пря­мые могут сов­па­дать, и тогда каж­дая точка будет ре­ше­ни­ем обоих урав­не­ний, а зна­чит си­сте­ма будет иметь бес­чис­лен­ное мно­же­ство ре­ше­ний. Для этого долж­ны вы­пол­нять­ся усло­вия: 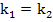и .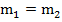

2. Спо­соб под­ста­нов­ки

При­мер 1:

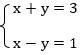
На дан­ном урав­не­нии можно про­де­мон­стри­ро­вать сразу несколь­ко спо­со­бов ре­ше­ния си­стем урав­не­ний.

1 спо­соб – спо­соб под­ста­нов­ки: вы­ра­зим во вто­ром урав­не­нии х и под­ста­вим по­лу­чен­ное вы­ра­же­ние в пер­вое урав­не­ние:

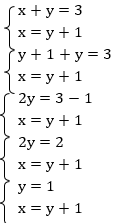
Под­ста­вим най­ден­ное зна­че­ние у во вто­рое урав­не­ние и най­дем зна­че­ние х:

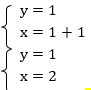
3. Спо­соб ал­геб­ра­и­че­ско­го сло­же­ния

2 спо­соб – спо­соб ал­геб­ра­и­че­ско­го сло­же­ния: вы­пол­ним сло­же­ние урав­не­ний:

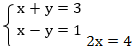
Из по­лу­чен­но­го урав­не­ния най­дем х:

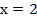
Те­перь вы­чтем из пер­во­го урав­не­ния си­сте­мы вто­рое:

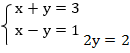
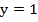
Таким об­ра­зом, мы по­лу­чи­ли ре­ше­ние си­сте­мы двумя спо­со­ба­ми, и это ре­ше­ние – точка с ко­ор­ди­на­та­ми (2; 1).

4. Си­сте­мы урав­не­ний с одним ре­ше­ни­ем

При­мер 2:

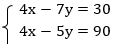
В дан­ном слу­чае удоб­нее при­ме­нить спо­соб ал­геб­ра­и­че­ско­го сло­же­ния, вы­чтем из вто­ро­го урав­не­ния пер­вое. По­лу­ча­ем:

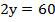
Най­дем зна­че­ние у:

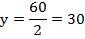
Под­ста­вим зна­че­ние у во вто­рое урав­не­ние и най­дем х:

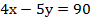
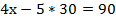
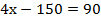
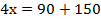
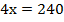
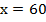
Ответ: (60; 30).

При­мер 3:

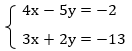
В дан­ной си­сте­ме нет пе­ре­мен­ных с оди­на­ко­вы­ми ко­эф­фи­ци­ен­та­ми, но мы можем их урав­нять са­мо­сто­я­тель­но, для этого вы­пол­ним пре­об­ра­зо­ва­ния:

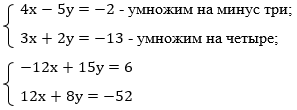
Вы­пол­ним сло­же­ние урав­не­ний:

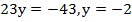
Под­ста­вим по­лу­чен­ное зна­че­ние у в пер­вое урав­не­ние и опре­де­лим зна­че­ние х:

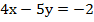
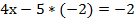
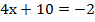
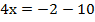
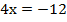
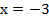
Ответ: (-3; -2).

5. Си­сте­мы, име­ю­щее бес­ко­неч­ное мно­же­ство или не име­ю­щие ре­ше­ний

При­мер 4:

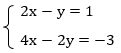
Раз­де­лим вто­рое урав­не­ние на два:

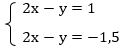
Вы­чтем из пер­во­го урав­не­ния вто­рое:

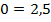
Оче­вид­но, что по­лу­чен­ное вы­ра­же­ние не за­ви­сит от зна­че­ний пе­ре­мен­ных си­сте­мы и не яв­ля­ет­ся вер­ным чис­ло­вым ра­вен­ством, зна­чит, си­сте­ма не имеет ре­ше­ний. В дан­ном слу­чае ре­ко­мен­ду­ет­ся гра­фи­че­ски до­ка­зать, что си­сте­ма не имеет ре­ше­ний, для этого из урав­не­ний за­пи­сать ли­ней­ные функ­ции, по­стро­ить их и по­ка­зать, что пря­мые па­рал­лель­ны.

При­мер 5:

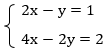
Оче­вид­но, что, если раз­де­лить вто­рое урав­не­ние на два, по­лу­чим пер­вое урав­не­ние:

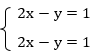
Мы по­лу­чи­ли два оди­на­ко­вых урав­не­ния, зна­чит, чтобы до­ве­сти ре­ше­ние си­сте­мы до конца, можем оста­вить одно: 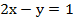; это ли­ней­ное урав­не­ние с двумя пе­ре­мен­ны­ми, гра­фик его – пря­мая линия, и оно имеет бес­чис­лен­ное мно­же­ство ре­ше­ний, а зна­чит и си­сте­ма имеет бес­чис­лен­ное мно­же­ство ре­ше­ний. Чтобы за­пи­сать ре­ше­ния, вы­ра­зим у: 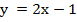, таким об­ра­зом, дадим ответ: х – любое число,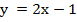

Гра­фи­че­ская ил­лю­стра­ция (рис. 1):

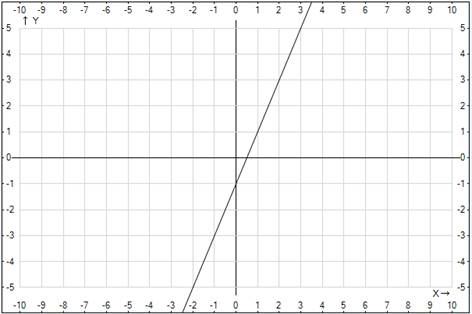
Рис. 1

6. Под­ве­де­ние ито­гов урока

Вывод: мы рас­смот­ре­ли си­сте­мы двух ли­ней­ных урав­не­ний с двумя пе­ре­мен­ны­ми, ва­ри­ан­ты и спо­со­бы их ре­ше­ния. Мы вспом­ни­ли неко­то­рые тер­ми­ны, по­ня­тия и свой­ства и ре­ши­ли при­ме­ры для за­креп­ле­ния тех­ни­ки.

Домашнее задание.

1. Решите систему тремя способами: сложением, подстановки, графическим: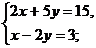

2. Сколько решений имеет система: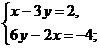

3. Решите систему любым способом: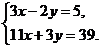

Урок 7:Алгебраические дроби. Арифметические операции над алгебраическими дробями.Основные понятия.

На данном уроке рассматривается понятие алгебраической дроби. С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить некий объект на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, что каждому достанется по 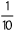части торта. В указанном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В таком случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деление на выражения с переменными) и их свойствами вы уже познакомились в 7 классе. Далее мы рассмотрим понятие рациональной дроби, а также допустимых значений переменных.

1. Определение и примеры алгебраических дробей

Рациональные выражения делятся на целые и дробные выражения.

Определение.Рациональная дробь – дробное выражение вида 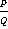, где 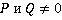– многочлены. 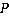– числитель, 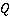– знаменатель.

Примерырациональных выражений: 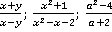– дробные выражения; 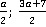– целые выражения. В первом выражении, к примеру, в роли числителя выступает 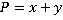, а знаменателя – .

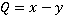Значение алгебраической дроби, как и любого алгебраического выражения, зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных 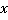и 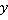, а во втором только от значения переменной .

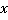Правило нахождения ОДЗ

Таким образом, можем сформулировать точное правило нахождения области допустимых значений дроби: для нахождения ОДЗ дроби необходимо и достаточно приравнять ее знаменатель к нулю и найти корни полученного уравнения.

Мы рассмотрели две основные задачи: вычисление значения дроби при указанных значениях переменных и нахождение области допустимых значений дроби.

Рассмотрим теперь еще несколько задач, которые могут возникнуть при работе с дробями.

Разные задачи и выводы

Пример 8. Докажите, что при любых значениях переменной дробь .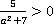

Доказательство. Числитель – число положительное. 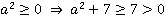. В итоге, и числитель, и знаменатель – положительные числа, следовательно, и дробь является положительным числом.

Доказано.

Пример 9.Известно, что 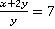, найти .

Решение. Поделим дробь почленно 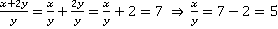. Сокращать на 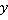мы имеем право, с учетом того, что 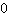является недопустимым значением переменной для данной дроби.

Ответ. .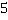

На данном уроке мы рассмотрели основные понятия, связанные с дробями. На следующем уроке мы рассмотрим основное свойство дроби.

Домашнее задание

1. Запишите рациональную дробь, областью определения которой является: а) множество 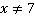, б) множество 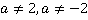, в) вся числовая ось.

2. Докажите, что при всех допустимых значениях переменной 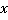значение дроби 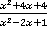неотрицательно.

3. Найдите область определения выражения 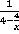. Указание: рассмотреть отдельно два случая: когда знаменатель нижней дроби равен нулю и когда знаменатель исходной дроби равен нулю.

Урок 8:Основное свойство алгебраической дроби.

На данном уроке будет рассмотрено основное свойство алгебраической дроби. Умение правильно и без ошибок применять это свойство является одним из важнейших базовых умений во всем курсе школьной математики и будет встречаться не только на протяжении изучения данной темы, но и практически во всех изучаемых в дальнейшем разделах математики. Ранее уже было изучено сокращение обыкновенных дробей, а на данном уроке будет рассмотрено сокращение рациональных дробей. Несмотря на довольно большое внешнее отличие, существующее между рациональными и обыкновенными дробями, у них очень много общего, а именно – и обыкновенным, и рациональным дробям присущи одинаковое основное свойство и общие правила выполнения арифметических действий. В рамках урока мы столкнемся с понятиями: сокращение дроби, умножение и деление числителя и знаменателя на одно и то же выражение – и рассмотрим примеры.

Примеры сокращения обыкновенных дробей

Для сокращения обыкновенных дробей мы прибегали к основной теореме арифметики, разлагали и числитель, и знаменатель на простые множители.

Определение. Простое число – натуральное число, которое делится только на единицу и само себя. Все остальные натуральные числа называются составными. 1 не является ни простым, ни составным числом.

Пример 1.а) 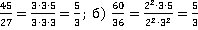, где множители, на которые разложены числители и знаменатели указанных дробей, являются простыми числами.

Ответ: ; .

Примеры сокращения алгебраических дробей

Следовательно, для сокращения дробей необходимо предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители. Т. е. следует владеть методами разложения многочленов на множители.

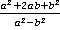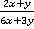Пример 2. Сократить дробь а) ,б) , в) .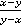

Решение. а) 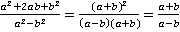. Необходимо заметить, что в числителе находится полный квадрат, а в знаменателе – разность квадратов. После сокращения необходимо указать, что 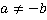, во избежание деления на ноль.

б) 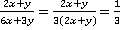. В знаменателе выносится общий числовой множитель, что полезно делать практически в любом случае, когда это возможно. Аналогично с предыдущим примером указываем, что .

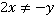в) 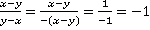. В знаменателе выносим за скобки минус (или, формально, 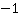). Не забываем, что при сокращении .

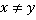Ответ. ; ; .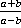

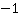Теперь приведём пример на приведение к общему знаменателю, делается это аналогично с обыкновенными дробями.

Пример на вычитание дробей с одинаковым знаменателем

Основное внимание на уроке мы уделили сложным случаям нахождения общих знаменателей у дробей. В дальнейшем это умение пригодится для проведения простейших операций с дробями, таких как сложение и вычитание. Рассмотрим один такой пример.

Пример 10.Найдите значение выражения 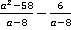при .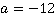

Решение.В подобных примерах подстановка числового значения в исходное выражение не является рациональной, сначала следует проделать все возможные операции в буквенном виде, т. е. упростить выражение, а уже затем подставлять числа. В данном случае необходимо вычесть дроби, они уже с одинаковыми знаменателями, поэтому поступаем, как и в случае обыкновенных дробей.

.

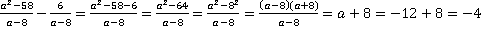Сокращение дроби на множитель 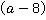мы имеем полное право проводить, т. к. значение подставляемой в дальнейшем переменной не входит в область недопустимых значений (см. урок №1). Недопустимым значением переменной в данном случае является: .

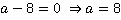Ответ. .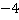

На следующих уроках мы более подробно рассмотрим технику сложения и вычитания алгебраических дробей и убедимся, что она аналогична методам работы с обыкновенными дробями.

Домашнее задание

1. Привести к общему знаменателю дроб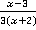и и .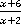

2. Привести к общему знаменателю дроб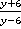и и .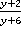

3. Привести к общему знаменателю дроб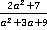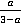и , и .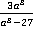

Урок 10:Сложение и вычитание алгебраических дробей с одинаковыми знаменателями (более сложные случаи).

Данный урок является логическим продолжением предыдущего, т. к. на прошлом уроке рассматривалась техника сложения и вычитания алгебраических дробей, а в рамках сегодняшнего урока будут рассмотрены более сложные случаи тех же операций над дробями. Дополнительно в рассматриваемых примерах будет делаться акцент на применение формул сокращенного умножения и на замену знака множителя на противоположный. Оказывается, что подобные процедуры могут существенно помочь при решении сложных примеров на сложение и вычитание алгебраических дробей.

Пример №1 на сложение/вычитание дробей с одинаковыми знаменателями

Вспомним изученное на прошлом уроке правило сложения и вычитания алгебраических дробей с одинаковым знаменателем:

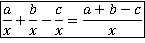
Примечательно то, что оно одинаково применимо и для простейших случаев, рассмотренных ранее, и для более сложных, которые мы сейчас разберем на примерах.

Пример 1.Сложить и вычесть указанные дроби: .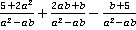

Решение.Очевидно, что указанные дроби уже с одинаковым (общим) знаменателем, и мы можем воспользоваться упомянутым ранее правилом их сложения/вычитания.

.

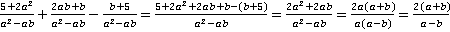Прокомментируем последовательность действий. В процессе применения правила сложения/вычитания дробей следует помнить, что такой знак, как минус перед дробью, относится ко всему числителю, и вычитать его необходимо в скобках. После приведения подобных слагаемых необходимо попытаться разложить знаменатель и числитель дроби на множители в надежде сократить на какой-то из них, что мы успешно и проделали. Затем при удачном стечении обстоятельств дробь сокращается, как в нашем случае, например, на 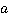. При этом стоит помнить, что любые сокращенные элементы необходимо учесть в области недопустимых значений переменных, так как они пропадают из дроби, и о них можно забыть. В нашем случае запишем, что .

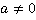Ответ. .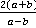

Пример №2 на сложение/вычитание дробей с одинаковыми знаменателями

Пример 2. Сложить и вычесть указанные дроби: .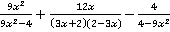

Решение.В указанном условии неочевидно, одинаковы ли знаменатели у дробей. Чтобы это проверить, разложим их на множители. При разложении на множители первого знаменателя 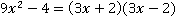видим, что он почти такой же, как и у второй дроби, противоположен только знак второго множителя. Чтобы привести знаменатели к одинаковому виду, вынесем минус из второго множителя второй дроби, и он окажется перед дробью, так как знак знаменателя и числителя относятся и ко всей дроби сразу:

.

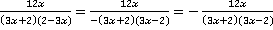Знаменатель третьей дроби тоже очень похож на знаменатель первой до разложения. Поступим с ним аналогично – вынесем минус и разложим на множители:

.

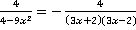Все полученные преобразования дробей подставим в исходное условие (знак перед третьей дробью получится положительным, т. к. «минус на минус дает плюс»).

.

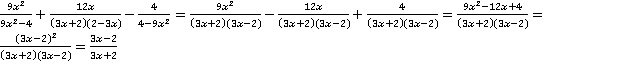В числителе воспользовались формулой квадрата разности. После сокращения учтем, что .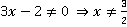

Ответ. .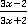

Рассмотрим теперь пример на применение умения складывать дроби с одинаковыми знаменателями в других целях.

Пример на применение сложение/вычитания дробей при доказательстве положительности выражения

Пример 3.Доказать, что выражение 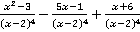принимает положительные значения при всех допусти