Определение линейной зависимости и линейной независимости системы векторов.

Рассмотрим набор из p n-мерных векторов, обозначим их следующим образом 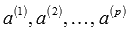. Составим линейную комбинацию этих векторов и произвольных чисел 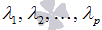(действительных или комплексных): 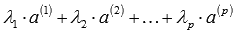. Отталкиваясь от определения операций над n-мерными векторами, а так же свойств операций сложения векторов и умножения вектора на число, можно утверждать, что записанная линейная комбинация представляет собой некоторый n-мерный вектор 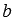, то есть, .

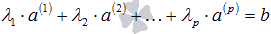Так мы подошли к определению линейной зависимости системы векторов .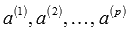

Определение.

Если линейная комбинация 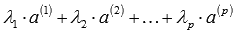может представлять собой нулевой вектор тогда, когда среди чисел 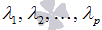есть хотя бы одно, отличное от нуля, то система векторов 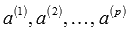называется линейно зависимой.

Определение.

Если линейная комбинация 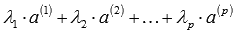представляет собой нулевой вектор только тогда, когда все числа 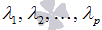равны нулю, то система векторов 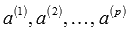называется линейно независимой.

К началу страницы

Свойства линейной зависимости и независимости.

На основании данных определений, сформулируем и докажем свойства линейной зависимости и линейной независимости системы векторов.

1. Если к линейно зависимой системе векторов 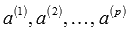добавить несколько векторов, то полученная система будет линейно зависимой.

Доказательство.

Так как система векторов 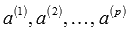линейно зависима, то равенство 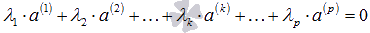возможно при наличии хотя бы одного ненулевого числа из чисел 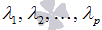. Пусть .

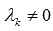Добавим к исходной системе векторов еще s векторов 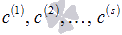, при этом получим систему 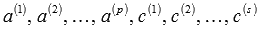. Так как 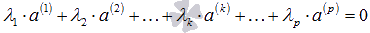и , то линейная комбинация векторов этой системы вида

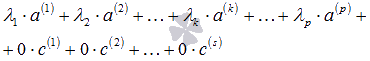
представляет собой нулевой вектор, а 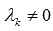. Следовательно, полученная система векторов является линейно зависимой.

2. Если из линейно независимой системы векторов 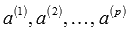исключить несколько векторов, то полученная система будет линейно независимой.

Доказательство.

Предположим, что полученная система линейно зависима. Добавив к этой системе векторов все отброшенные векторы, мы получим исходную систему векторов. По условию – она линейно независима, а в силу предыдущего свойства линейной зависимости она должна быть линейно зависимой. Мы пришли к противоречию, следовательно, наше предположение неверно.

3. Если в системе векторов 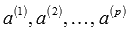есть хотя бы один нулевой вектор, то такая система линейно зависимая.

Доказательство.

Пусть вектор 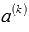в этой системе векторов является нулевым. Предположим, что исходная система векторов линейно независима. Тогда векторное равенство 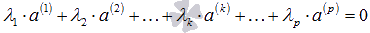возможно только тогда, когда 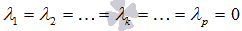. Однако, если взять любое 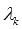, отличное от нуля, то равенство 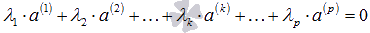все равно будет справедливо, так как 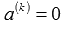. Следовательно, наше предположение неверно, и исходная система векторов линейно зависима.

4. Если система векторов 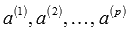линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов 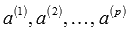линейно независима, то ни один из векторов не выражается через остальные.

Доказательство.

Сначала докажем первое утверждение.

Пусть система векторов 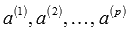линейно зависима, тогда существует хотя бы одно отличное от нуля число 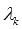и при этом верно равенство 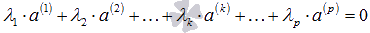. Это равенство можно разрешить относительно 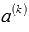, так как 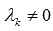, при этом имеем

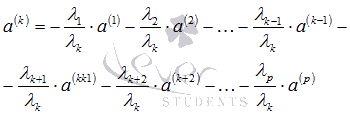
Следовательно, вектор 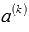линейно выражается через остальные векторы системы 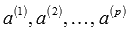, что и требовалось доказать.

Теперь докажем второе утверждение.

Так как система векторов 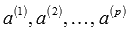линейно независима, то равенство 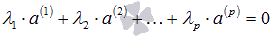возможно лишь при .

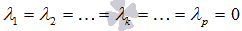Предположим, что какой-нибудь вектор системы 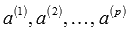выражается линейно через остальные. Пусть этим вектором является 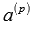, тогда 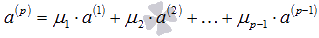. Это равенство можно переписать как 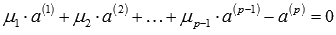, в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором 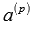отличен от нуля, что указывает на линейную зависимость исходной системы векторов. Так мы пришли к противоречию, значит, свойство доказано.

Из двух последних свойств следует важное утверждение:
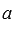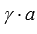если система векторов содержит векторы и , где 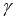– произвольное число, то она линейно зависима.

Определение 1. Числовым полем 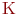называется множество чисел 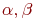, если 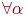, 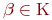числа 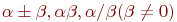также принадлежат этому множеству.

Определение 2. Множество 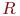называется линейным или векторным пространством над полем 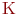, если для любых двух его элементов 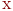и 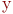определена сумма 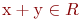и для каждого элемента 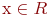и каждого числа 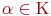определено произведение 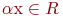так, что выполнены следующие условия:

1. ;

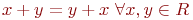2. ;

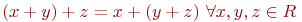3. существует такой нулевой элемент 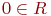, что ;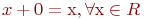

4. для каждого элемента 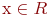существует такой элемент -x (называется противоположным х ), что x + (-х) = 0 ;

5. ;

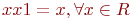6. ;

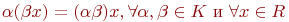7. ;

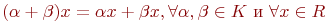8. .

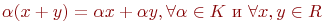Эти условия в математике называют аксиомами линейного пространства.

Традиционно элементы линейного пространства называют векторами, хотя по своей конкретной природе они могут быть вовсе не похожи на привычные для нас направленные отрезки.

Приведем еще несколько примеров линейных пространств.

1. Множество многочленов степени не выше n с вещественными коэффициентами.

2. Множество свободных векторов в трехмерном пространстве, рассматриваемые в аналитической геометрии. Это пространство обозначается V₃.

3. Множество всех матриц размером m x n.

4. n - мерное арифметическое пространство. Это множество всех упорядоченных наборов из n чисел, например х = (х₁, х₂, ..., х_n), у = (у₁, у₂, ..., у_n), для которых определены операции сложения и умножения на число 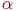по правилам:

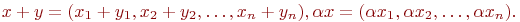
Определение 3. Набор n чисел х = (х₁, х₂, ..., х_n) называется n - мерным вектором арифметического пространства.

Определение 4. Числа х₁, х₂, ..., х_n, составляющие n -мерный вектор х, называются координатами вектора.

Определение 5. Если координаты всех n - мерных векторов вещественные, то арифметическое пространство называют вещественным и обозначаютR_n. Если координаты векторов комплексные, то пространство называют комплексным и обозначают С_n.

Билет 5

Базисом линейного пространства называется система векторов 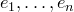такая, что

1) 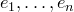— система образующих пространства ;

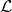2) 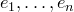— линейно независимая система.

Теорема. Система векторов 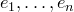является базисом линейного пространства 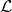тогда и только тогда, когда это максимальная линейно независимая система векторов.

Доказательство.

Пусть 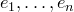— базис 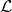. Тогда по определению 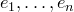— линейно независимая система векторов. Любой вектор представим в виде линейной комбинации 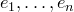, т.е. любая большая система векторов линейно зависима, т.е. для векторов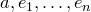

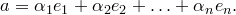
Значит, базис — максимальная линейно независимая система.

Пусть 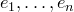— максимальная линейно независимая система. Второе свойство базиса выполняется. Любая большая система векторов линейно зависима:

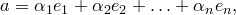
т.е. каждый вектор является линейной комбинацией векторов этой системы — выполнено первое свойство.