Операции над высказываниями.
Пусть имеется некоторая совокупность высказываний, которые назовем элементарными. Исходя из этих высказываний, можно строить новые высказывания с помощью так называемых логических операций.
Определение.Отрицанием высказывания Р называется новое высказывание 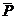
(илиù Р ), которое считается истинным, если высказывание Р ложно и считается ложным, если Р истинно. Высказывание 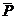 читается: ”неверно, что…”.
читается: ”неверно, что…”.
Пример. Высказывание Р: “3<5”.Высказывание 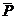 :”неверно, что 3<5”.
:”неверно, что 3<5”.
Определение.Конъюнкцией высказываний P и Q называется новое высказывание РÙQ (или P&Q), которое считается истинным, если истинны оба высказывания P и Q и ложным во всех остальных случаях.
Пример. Высказывания Р: 1<20 и Q: 1>-2, то высказывание РÙQ:-2<1<20.
Определение.Дизъюнкцией высказываний P и Q называется новое высказывание PÚQ, которое истинно в тех случаях, если хотя бы одно из высказываний P или Q истинно, и ложно, если ложны оба высказывания.
Пример. Высказывания X:”1>100”и Y:”5>2”, то высказывание XÚY (”1>100” или ”5>2”) истинно, так как истинно Y.
Определение.Импликацией высказываний P и Q называется высказывание P®Q, ложное лишь в том случае, когда Р истинно, а Q ложно.
Высказывание “P®Q” читается : “Если Р то Q” или “Из Р следует Q”. При этом высказывание Р- посылка (или условие), а Q-заключение (следствие).
Пример. Высказывание “Если 2<5, то 7<3” является импликацией высказываний “2<5”(посылка) и “7<3”(заключение). Высказывание ложно, т.к. из истинной посылки “2<5”сделано ложное заключение “7<3”.
Определение. Эквиваленцией высказываний P и Q называется высказывание P«Q (читается “P эквивалентно Q” или “P тогда и только тогда, когда Q”), а истинно в том и только том случае, когда P и Q одновременно истинны или одновременно ложны.
Операции “Конъюнкция”, “Дизъюнкция”, “Импликация”, “Эквивалентность”, можно рассматривать как функции двух логических переменных x и y. Значения функций принадлежат тому же числовому множеству {0; 1}, что и значения логических переменных, такие функции называются булевыми функциями.
Сводная таблица истинности логических операций над высказываниями:
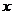 | 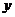 | 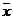 | 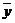 | 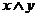 | 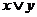 | 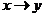 | 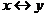 | |
Законы алгебры логики.
1а 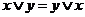 | 1б 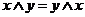 коммутативность коммутативность |
2а 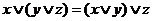 | 2б 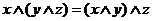 ассоциативность ассоциативность |
3а 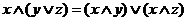 | 3б 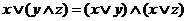 дистрибутивность дистрибутивность |
4а 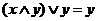 | 4б 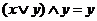 закон поглощения закон поглощения |
5а 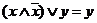 | 5б 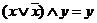 закон Моргана закон Моргана |
Контактные схемы.
Одним из приложений булевых функций является анализ и синтез так называемых контактных схем. Будем рассматривать переключательные схемы электрической цепи.
Между источником питания и потребителем может быть замыкающий и размыкающий цепь контакт, либо цепь контактов, соединенных последовательно или параллельно. Каждому контакту поставим в соответствие логическую переменную, которая примет значение 1, если контакт в рассматриваемый момент времени замыкает цепь, и значение 0, если цепь разомкнута.

Поместим между источником и потребителем тока два контакта, соединенные последовательно (рис. b). Соответствующие им логические переменные обозначим через х1 и х2. Для такой цепи условие прохождения тока описывается конъюнкцией х1Ùх2.
Если контакты соединены параллельно (рис с), то цепь замкнута, когда хотя бы один из контактов замкнут, и разомкнута, когда оба они разомкнуты. Очевидно, работа в цепи в этом случае описывается дизъюнкцией х1Úх2.
Контакты не всегда независимы друг от друга. Можно устроить так, чтобы замыкались и размыкались одновременно. В этом случае контакты называют идентичными и им ставят в соответствие одинаковые логические переменные.
Однако можно устроить так , что при замыкании одного контакта другой размыкается. В этом случае контакты называют инверсными. Любую формулу логики высказываний можно моделировать в виде переключательной схемы.
Пример. Совершенной дизъюнктивной нормальной форме (с.д.н.ф.) F(x,у,z) 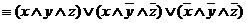 , составленной по таблице истинности, соответствует переключательная схема вида:
, составленной по таблице истинности, соответствует переключательная схема вида:
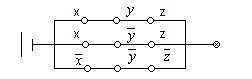
Для соответствующей совершенной конъюнктивной нормальной формы (с.к.н.ф.)
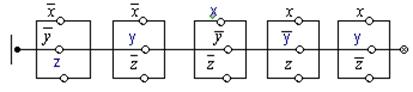 |
F(x,y,z)
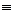
 переключательная схема имеет вид:
переключательная схема имеет вид: