Круги Эйлера. Алгебра множеств.
Для наглядного изображения соотношений между подмножествами некоторого универсального множества U используются круги Эйлера. Множество U обычно представляется множеством точек прямоугольника, а его подмножества изображаются кругами или другими простыми областями внутри этого прямоугольника. Непересекающиеся множества изображаются непересекающимися областями, а подмножествам соответствуют области, целиком располагающиеся внутри другой области. Дополнение множества А (до U), т.е. множество 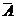 , изображается той частью прямоугольника, которая вне круга, изображающего
, изображается той частью прямоугольника, которая вне круга, изображающего 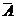 .
.
Рассмотрим операции над множествами с помощью диаграмм Эйлера-Венна.
 | 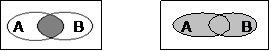 | ||
|
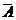 A ÇB A ÈB
A ÇB A ÈB
Пусть А, В, СÎU, тогда имеют место следующие соотношения:
| 1a AÈB=BÈA | 1b AÇB=BÇA (коммутативность) |
| 2a AÈ(BÈC)=(AÈB)ÈC | 2b AÇ(BÇC)=(AÇB)ÇC (ассоциативность) |
| 3a AÇ(BÈC)=(AÇB)È(AÇC) | 3b AÈ(BÇC)=(AÈB)Ç(BÈC) (дистрибутивность) |
Законы поглощения:
| 4a (AÇB)ÈB=B | 4b (AÈB)ÇB=B |
5a (AÇ 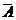 )ÈB=B )ÈB=B | 5b (AÈ 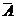 )ÇB=B )ÇB=B |
Дополнительные свойства:
1a 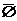 =U =U | 1b 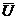 = = 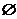 |
2a AÈ 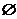 =A =A | 2b AÇU=A |
3a AÈ 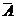 =U =U | 3b AÇ 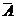 = = 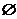 |
4a 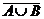 = = 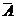 Ç Ç 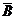 | 4b 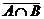 = = 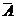 È È 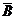 |
Мощность множества.
Конечные множества можно сравнивать по количеству элементов, содержащихся в них. Для сравнения по насыщенности бесконечных множеств используется принцип сравнения. Между множеством точек гипотенузы прямоугольного треугольника и множеством точек катета можно установить соответствие таким образом, что каждой точке гипотенузы будет соответствовать точка катета и при этом разным точкам гипотенузы соответствуют разные точки катета. Соответствие устанавливается с помощью прямой, проведенной параллельно другому катету через взятую на гипотенузе точку М.
Определение. Говорят, что между элементами А и В установлено взаимно однозначное соответствие, если указано правило, по которому каждому элементу аÎА сопоставлен один элемент вÎВ, называемый образом а, причем выполнены следующие два условия: 1) любые два различные элемента из А имеют различные образы; 2) каждый элемент из В является образом некоторого элемента из А.
Определение. Два множества А и В называются эквивалентными или имеющими одинаковую мощность (обозначается А ~ В), если между их элементами может быть установлено взаимно однозначное соответствие.
Примеры эквивалентных бесконечных множеств:
1. Множество N всех натуральных чисел и множество N1 всех целых отрицательных чисел эквивалентны: nÎN, -nÎN1, N~N1
2. Множество N эквивалентно множеству P положительных четных чисел:
nÎN, 2nÎP, N~P.
3. Множество действительных чисел и множество чисел интервала G=( 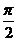 ; -
; - 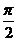 )
)
эквивалентны между собой. Эквивалентность этих множеств легко проверить с помощью соответствия у=tgx (xÎG,yÎR).
4. Любые два отрезка эквивалентны между собой. Взаимно однозначное соответствие между точками отрезков ОА и ОВ устанавливается с помощью прямых,
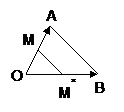 проводимых параллельно отрезку АВ. Способ установления взаимно однозначного соответствия между элементами (точками) показан на рисунке.
проводимых параллельно отрезку АВ. Способ установления взаимно однозначного соответствия между элементами (точками) показан на рисунке.
Два множества, порознь эквивалентные третьему, эквивалентны между собой: Если А~B и B~C, то А~B. Поэтому любой отрезок эквивалентен, например, отрезку [0;1].
Множества, эквивалентные множеству всех вещественных чисел из отрезка [0;1] называют множеством мощности континуум (сокращенно мощности С). Значит, множество чисел любого числового отрезка имеет мощность С. В частности, множество всех вещественных чисел R~( 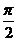 ; -
; - 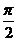 )~[0;1] имеет мощность С.
)~[0;1] имеет мощность С.
