Тема 1.1.2 Равные множества. Круги Эйлера
Понятие разбиения множества на попарно непересекающиеся подмножества.
Пересечение, объединение, разность множеств.
(1ч.)
Равенство множеств. Ø.
Понятие равенства множеств совпадает с понятием равенства мешков. Равные множества отличаются только порядком элементов.
ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ
(1ч.)
Подмножество. 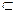 ,
, 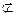
1) ввести понятие подмножества как части множества. Научить использовать 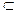 ,
, 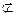 .
.
2) Рассмотреть частные случаи А 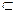 А, Ø
А, Ø 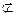 А.
А.
3) Разбиение множества на части (классы).
Понятие подмножества аналогично понятию части. Но есть и отличия. Говорить, что часть всегда меньше целого, в теории же множеств любое множество является подмножеством самого себя: А 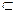 А, т.к. пустое множество не содержит элементов, то не может являться подмножеством (хотя в теории множеств Ø
А, т.к. пустое множество не содержит элементов, то не может являться подмножеством (хотя в теории множеств Ø 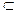 любому множеству).
любому множеству).
N - множество натуральных чисел;
Z - множество целых чисел;
Q - множество рациональных чисел;
R - множество действительных чисел.
Упражнения
1. Назовите три элемента множества:
а) учебных предметов, изучаемых в начальной школе;
б) четных натуральных чисел;
в) четырехугольников.
2. Запишите, используя символы:
а) Число 14 - натуральное;
б) Число -7 не является натуральным;
в) Число 0 - рациональное;
3. Прочитайте следующие высказывания и укажите среди них верные:
а) 100 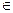 N; г) 5,36
N; г) 5,36 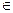 Q; ж) -7,3
Q; ж) -7,3 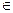 R;
R;
6)-8 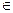 Z; f)102
Z; f)102 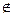 R; з)
R; з) 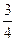
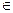 N;
N;
4
B)-12 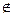 N; e)
N; e) 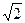
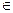 Q; и) 0
Q; и) 0 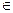 N.
N.
4. Запишите множество букв в слове «математика» и множество цифр в записи числа 5125353.
Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются.
Например, если А - {а, Ъ, с, d, е}, В - {b, d, k, т), С =, {х, у, z}, то можно утверждать, что множества А и В пересекаются, так как имеют общие элементы b и d, а множества А и С, В и С не пересекаются, поскольку не имеют общих элементов.
Рассмотрим теперь множества А = {а, Ъ, с, d, e} и В = {с, d, e}. Они пересекаются, и, кроме того, каждый элемент множества В является элементом множества А. В этом случае говорят, что множество В включается в множество А или что множество В является подмножеством множества А и пишут В 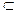 А.
А.
Определение. Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество считают подмножеством любого множества. Любое множество является подмножеством самого себя.
Определение. Множества А и В называются равными, если А 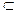 В и В
В и В 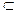 А.
А.
| Из определения следует, что равные множества состоят из одних и тех же элементов и что порядок записи элементов множества не существен. Отношения между множествами наглядно представляют при помощи особых чертежей, называемых кругами Эйлера1. |
чертежей, кот-е наз-ся кругами ЭЙЛЕРА:
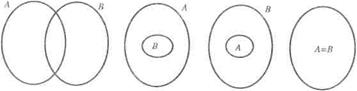
А б в г
Пример Определим, в каких отношениях находятся множества А и В. Изобразим эти отношения при помощи диаграмм Эйлера—Венна, если:
а) А — множество гласных букв русского алфавита;
В - множество звонких согласных.
б) А — множество натуральных чисел, кратных 3;
В — множество натуральных чисел, кратных 9.
Решение, а) Поскольку множества А и В не имеют общих элементов, то они не пересекаются. Поэтому на диаграммах Эйлера— Венна они будут изображаться так, как два круга не имеющих общих точек.
б) Представим множества А и В в следующем виде:
А = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, ...};
В = {9, 18, 27, 36, ...}.
Из приведенных записей очевидно, что множества А и В пересекаются. Кроме того, каждый элемент множества В принадлежит множеству А, т.е. В С А. (рис.под буквой а)
