Общее решение этих уравнений будет содержать шесть произвольных постоянных.
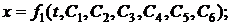
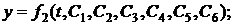(16)
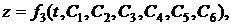
Итак мы получили шесть уравнений, которые имеют шесть неопределенных постоянных. Если задана сила она определяет не одно движение
Как видим ДУ движения точки при заданной силе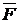 
, определяет не одно движение , а целый класс движений.
Возникает вопрос, почему так получается, ДУ известно, силы действующие известны и тем не менее определяем бесчисленное множество решений.
Рассмотрим пример, а потом я вам поясню как это получается, с точки зрения физики.
Пусть материальная точка – это мел.
Если это мел падает вниз под действием силы тяжести – это одно движение, Если при падении мела вниз с определенной высоты сообщить ему скорость, то он будет падать по параболе.
Можно бросить мел вверх сообщив ему ускорение, тогда он движется под углом к горизонту.
 |
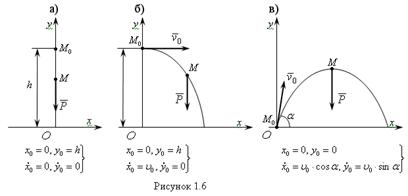Во всех трех задачах сила действует одна и та же, а движения тем не менее происходят разные.
Выходит движения зависят не только от действующей силы, но и от того ,где точка была в начале движения и какая у него при этом была скорость, т.е. от начального состояния.
Почему? Как это объяснить?
Сила определяет только ускорение, а скорость и положение точки на траектории определяют не только действующие силы, но и начальные положения и начальная скорость.
Таким образом, для того, чтобы задача была вполне определенной необходимо присоединить к этим уравнениям начальные условия
Чтобы получить вполне определенный закон движения точки к ДУ необходимо присоединить начальные условия.
Сколько этих условий будет?
Шесть, определяющие положение точки в начальный момент времени и скорость.
при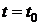 
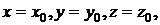(17)
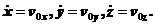
Здесь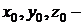 
начальные координаты;
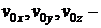проекции начальной скорости точки.
Что же мы должны делать при решении конкретной задачи. Уравнения (15) проинтегрировать , т.е. построить какое-то частное решение, которое бы удовлетворяло бы этим уравнениям и подставить начальные условия.
С точки зрения математики такая задача называется задачей Коши.
Следовательно данная задача механики сводиться к известной задачи Каши из теории ДУ( О.Коши (1780-1857) – выдающийся французский математик.)
Для того, чтобы сформулировать вторую задачу динамики что необходимо знать?
Массу, силу, а необходимо найти закон движения и неизвестную реакцию.
Сформулируем вторую задачу динамики для несвободной точки.
В случае несвободной материальной точки, во второй основной задаче динамики, требуется по заданным массе, активной силе, начальному положению и начальной скорости точки определить движение точки и реакцию связей .
Какая задача более сложная для свободной, или не свободной?
Эта задача для несвободной материальной точки принципиально отличается от подобной задачи для свободной материальной точки.
При решении второй основной задачи динамики для свободной точки главное правильно составить дифференциальные уравнения движения, после чего их всегда можно проинтегрировать точно или приближёнными способами, известными из теории дифференциальных уравнений.
Для несвободной точки, мы не можем приступить непосредственно к интегрированию ДУ.
Дело в том, что в эти уравнения входят шесть неизвестных: три координаты x, y, z точки и три проекции Nx, Ny, Nz силы реакции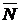 
, которая зависит не только от вида связи и активной силы 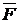, но и от самого движения точки. Поэтому прежде всего нужно каким бы то ни было способом исключить эту реакцию и только после этого можно приступить к интегрированию дифференциальных уравнений, уже не содержащих неизвестную реакцию, а затем по найденным уравнениям движения
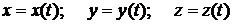
можно легко найти Nx, Ny, Nz
РС
При решении задач все силы можно разделить на силы зависящие от положения, скорости и времени.
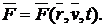
Примерами сил, зависящих от положения точки, являются упругая сила пружины, силы всемирного тяготения, кулоновы силы взаимодействия между зарядами.
К силам, зависящим от скорости, относятся силы сопротивления различных сред.
Сила, вызывающая колебания неуравновешенного мотора на упругом основании, служит примером силы, являющейся периодической функцией времени. К этому же классу сил относятся гидродинамические силы, действующие на винт корабля.